Рисование геометрических тел

Изучение и рисование геометрических тел в учебном академическом рисунке является основой для освоения принципов и методов изображения более сложных форм.

Обучение изобразительным искусствам требует строгого соблюдения последовательности усложнения учебных задач и многократных повторений для овладения техникой. Наиболее подходящей формой для усвоения принципов построения рисунка являются геометрические тела, имеющие в своей основе ясные конструктивные строения. На простых геометрических телах легче всего понять и усвоить основы объемно-пространственной конструкции, передачи форм в перспективном сокращении, закономерности светотеней и пропорциональные отношения.

Упражнения по рисованию простых геометрических тел позволяют не отвлекаться на детали, имеющиеся в более сложных формах, таких, как архитектурные объекты и тело человека, а всецело сосредоточиться на главном - изобразительной грамоте.

Правильно понятые и усвоенные закономерности при изображении простых форм должны способствовать более осознанному подходу к рисованию сложных форм в последующем.

Для того чтобы научиться грамотно и правильно изображать форму предмета, необходимо осознать скрытую от глаз внутреннюю структуру предмета - конструкцию. Под словом "конструкция" (от латинского construct) подразумевается "строение", "структура", "план", то есть взаимное расположение частей предмета и их соотношение. Это важно знать и понимать при изображении любых форм. Чем сложнее форма (независимо от материала, фактуры и цвета предмета), тем больше и серьезнее студентам придется изучать внутреннее строение натурной модели. Гак, например, при рисовании живой натуры - головы или фигуры человека, помимо знания общеконструктивных особенностей непременно следует знать и пластическую анатомию. Поэтому без ясного понимания строения формы и характера предмета невозможно грамотно освоить рисунок.

При изображении пространственных форм, кроме знания закономерностей строения конструкции, необходимы знания о законах перспективы, пропорции, светотени. Вопросы, касающиеся перспективы и пропорции, подробно освещены в разделах "Пропорции" и "Основы перспективы".

Для правильного изображения натурной модели студентам необходимо еще раз напомнить о необходимости приучить себя всегда анализировать натуру, ясно представлять ее внешнее и внутреннее строение. К сожалению, как показывает практика, многие студенты ограничиваются лишь поверхностным впечатлением, не углубляясь в суть строения формы предмета. В искусстве, как и в любой науке, к изучению натурного предмета необходимо подходить с научной точки зрения. Подходить к работе следует осознанно, не довольствуясь копированием внешних форм, которые видит глаз. Такое рисование не будет способствовать успешному выполнению работ по изображению как простых, так и сложных форм.

Рисование геометрических форм малоопытным рисовальщикам кажется на первый взгляд достаточно легким. Но это далеко не так. Не имея достаточного опыта в рисовании, студенты легко привыкают к механическому копированию. Поэтому при изображении более сложных форм можно легко запутаться. Для более уверенного овладения рисунком прежде всего необходимо освоить методы анализа форм и принципы геометрического построения простых тел.

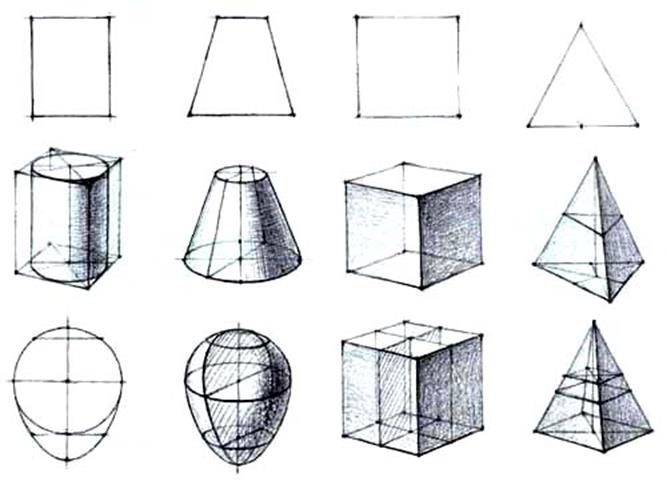
Рис.34

Любая форма состоит из плоских фигур: прямоугольников, треугольников, ромбов, трапеций и других многоугольников, которые отграничивают ее от окружающего пространства. Задача заключается в том, чтобы правильно понять, как эти поверхности сочетаются между собой, образуя форму. Для правильного ее изображения студентам необходимо научиться рисовать такие фигуры в перспективе, чтобы без особого труда выделять на плоскости объемные тела, ограниченные этими плоскими фигурами. Плоские геометрические фигуры служат основой понимания конструктивного построения объемных тел. Так, например, квадрат дает представление о построении куба, прямоугольник - о построении призмы параллелепипеда, треугольник - пирамиды, трапеция - усеченного конуса, круг представляется шаром, цилиндром и конусом, а эллипсовидные фигуры - шарообразными (яйцевидными) формами (рис.34).

Все предметы имеют объемно-пространственные характеристики: высоту, длину и ширину. Для определения и изображения их на плоскости пользуются точками и линиями. Точками определяются характерные узлы конструкции предметов, ими устанавливается взаимное пространственное расположение узлов, характеризующее конструкцию формы в целом.

Линия является одним из основных изобразительных средств. Линиями обозначают контуры предметов, образующие их форму. Ими обозначают высоту, длину, ширину, конструктивные оси, вспомогательные, определяющие пространства линии, линии построения и многое другое.

Для основательного изучения геометрические формы лучше всего следует рассматривать в виде прозрачных каркасных моделей. Это позволяет лучше проследить, понять и усвоить основы пространственного построения конструкций и перспективного сокращения форм геометрических тел: куба, пирамиды, цилиндра, шара, конуса и призмы. Вместе с тем, такой прием в значительной степени облегчает построение рисунка, в котором отчетливо прослеживаются все пространственные углы, ребра, грани тела, независимо от их поворотов в пространстве и в перспективном сокращении. Каркасные модели позволяют развить у студентов объемно-пространственное мышление, тем самым способствуя правильному изображению геометрической формы на плоскости бумаги.

Для основательного закрепления в сознании студентов объемно-пространственного представления о строении этих форм было бы наиболее эффективным выполнить их своими руками. Модели можно сделать без особого труда из подручных материалов: обыкновенной гибкой алюминиевой, медной или любой другой проволоки, деревянных или пластмассовых реек. В последующем, в целях усвоения закономерностей светотени, можно будет изготовить модели из бумаги или тонкого картона. Для этого необходимо сделать заготовки - соответствующие развертки или отдельно вырезанные плоскости для склеивания. Не менее важен сам процесс моделирования, который больше принесет пользы для осознания обучающимися сущности строения той или иной формы, чем использование уже готовой модели. Для изготовления каркасных и бумажных моделей потребуется немало времени, поэтому в целях его экономии не следует делать модели большого размера - достаточно, если их габариты не будут превышать трех, четырех или пяти сантиметров.

Поворачивая изготовленную бумажную модель под разными углами к источнику света, можно проследить за закономерностями света и тени. При этом следует обратить внимание на изменение пропорциональных отношений частей предмета, а также на перспективное сокращение форм. Приближая и отдаляя модель от источника света, можно увидеть, как меняется контрастность освещения на предмете. Так, например, при приближении к источнику света свет и тень на форме приобретают наибольшую контрастность, а по мере удаления становятся менее контрастными. Причем, близлежащие углы и грани будут наиболее контрастными, а углы и грани, находящиеся в пространственной глубине,

- менее контрастными. Но самое главное на начальном этапе рисования
- это умение правильно отображать объемно-пространственную конструкцию форм с помощью точек и линий на плоскости. Это является основополагающим принципом в освоении рисунка простых геометрических форм, а также при последующем изучении более сложных форм и осознанном их изображении.

Для последовательного изучения, анализа форм и выполнения рисунка геометрических тел следует рассмотреть приемы и принципы их построения на плоскости.

В целях соблюдения последовательности в работе над рисунком, основанной на принципе "от простого к сложному", необходимо вначале изучить простые геометрические тела: куб, призму, пирамиду, цилиндр.

Рисование куба

Куб является одним из самых простых геометрических тел. Чтобы лучше понять геометрическую форму куба, его пространственную конструктивную схему (структуру), рассмотрим каркас куба. Это дает возможность ясно представить объемно-пространственную характеристику его формы, позволяет видеть его конструктивные узлы - точки, невидимые на обычных телах.

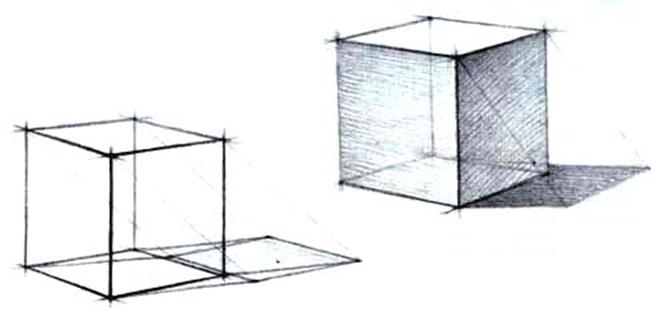
Рис.35

Куб характеризуется восемью точками на углах и двенадцатью линиями ребер. Соотношения сторон куба составляют пропорцию 1:1:1. Для того чтобы куб выглядел достоверно в трехмерном изображении, студентам следует определить такую точку зрения, при которой предмет выглядит достаточно убедительным в объеме. Изображение каркаса куба производится с учетом его пропорций, по законам перспективы. При обычном взгляде сверху (в ракурсе) основание каркаса куба (квадрат) выглядит ромбом. Перспективное построение куба в соответствии с его поворотом следует начинать с квадрата основания, т.е. с его плана, лежащего в горизонтальной плоскости, уходящей в глубину до линии горизонта (рис.35). Чтобы получить нижнее основание (ромб), необходимо обозначить четыре точки и соединить их четырьмя линиями. Из точек основания проводят вертикальные линии - ребра. Для завершения построения, как и в первом случае, обозначают четыре точки и, соединив их четырьмя линиями, получают верхнее основание куба (ромб). Необходимо отметить одну немаловажную деталь, касающуюся характера линий при построении изображения на плоскости. Кроме соблюдения пропорции и перспективы, линии, определяющие пространственную глубину, должны быть проведены в различной степени контрастности. Линии близлежащих ребер следует проводить более контрастно, чем тех, что находятся в перспективном удалении. Причем разница линий должна быть предельно различимой в соответствии с пространственной глубиной.

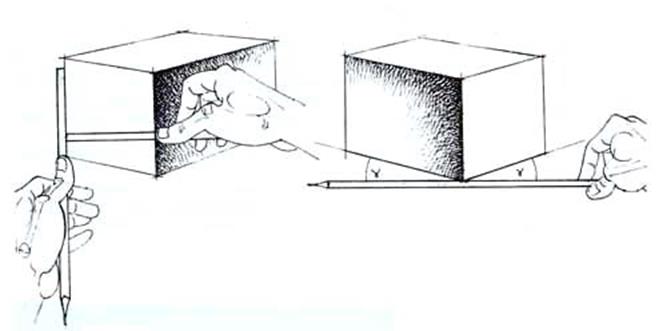
Рис.36. Измерение пропорциональных величин

Перспективный рисунок куба может быть сравнительно легко построен и проверен различными способами. Одним из таких способов являются приемы, давно применяемые на практике старыми мастерами, - это сравнение и визирование. Для определения основных больших размеров предмета в рисунке важны видимые, перспективно измененные их соотношения, а не реальные размеры объекта и его частей. Так, например, отношение ширины какой-либо грани к высоте переднего ребра вымеряют карандашом на вытянутой руке, перпендикулярно лучу зрения, совмещая тыльную сторону карандаша с краем формы предмета измеряемой части модели. При этом большим пальцем отмечают видимые размеры частей предмета. Не меняя положения большого пальца на вытянутой руке и поворачивая карандаш в вертикальном положении, соотносят этот отрезок карандаша с вертикальным ребром куба, определяя визуально их различия (рис.36).

Работая над конструктивным построением куба, нужно внимательно следить за его перспективным сокращением. Для этого необходимо мысленно представить форму с данной точки зрения в плане, т.е. увидеть ее сверху. Такое представление дает возможность лучше разобраться, как согласуются плоскости между собой и в целом. В рисовании с натуры важно правильно передать не только видимые соотношения величин, но и величины углов между основаниями двух видимых граней, т.е. перспективные ракурсы.

Для их правильного определения следует сделать проверку механическим способом визирования. Держа карандаш за кончик на вытянутой руке, нужно совместить линию самого карандаша с вершиной переднего нижнего угла основания предмета и определить на глаз угол наклона предмета в перспективе. Запомнив увиденное, проведите на своем рисунке соответствующую вспомогательную горизонтальную линию. Сравнивая величину наклона (угла) правой и левой сторон модели, уточните рисунок. При необходимости дополнительного уточнения следует повторить проверку. На рис.36 наглядно показаны способы измерения размеров и проверки перспективного наклона горизонтальных ребер куба. Заметим, что, рисуя с натуры, не нужно злоупотреблять приемом визирования, поскольку он носит чисто механический характер определения размеров и не способствует развитию глазомера. Им пользуются на начальной стадии обучения рисованию с натуры, и он должен служить лишь для вспомогательного контроля и проверки уже выполненных работ.

При положении куба со смещенным несколько вправо от центра передним вертикальным ребром горизонтальные ребра его левой грани в перспективе будут приближаться к горизонтали, а ребра правой, наоборот - отклоняться от нее. Следовательно, чем больше сокращается правая грань, тем меньше будет сокращение левой и наоборот. Это обусловлено взаимным прямоугольным расположением плоскостей куба.

Для лучшего усвоения материала по изучению геометрических тел необходимо выполнить академическое задание по рисунку куба. Усваивая закономерности строения формы куба, следует иметь в виду, что за их соблюдением нужно следить на протяжении всего процесса рисования с натуры. Работа над длительным рисунком требует соблюдения методической последовательности как в анализе строения формы, так и в процессе построения изображения. Это дает возможность закреплять отдельные этапы учебного рисунка, без чего невозможно понять основной смысл учебного материала. При этом следует отметить, что членение процесса работы над рисунком на отдельные этапы носит достаточно условный характер. Это связано с ошибками в решении задач, которые могли быть допущены на предыдущем этапе, и необходимостью их исправления в процессе работы.

Рис.37. Последовательность работы над рисунком куба

Рассмотрим последовательность выполнения рисунка куба (рис.37).

1. Рисунок начинают с композиционного размещения предмета на листе. Изображение намечают легкими линиями с боков, сверху и снизу. С учетом ракурса, пропорции и перспективы находят и определяют основные конструктивные точки вершин углов куба.
2. С учетом перспективных сокращений по конструктивным точкам вершин углов намечают общую форму конструкции куба.
3. Уточняют пропорции и перспективное построение объемно-пространственной формы куба. Определяют границы собственной и падающей теней.
4. С помощью светотональных отношений выявляют объемную форму куба. Наносят собственные и падающие тени. Определяют фон.
5. Полная тональная проработка формы. Работа светотональными отношениями: свет, тень, полутень и рефлекс.
6. Подведение итогов. .Проверка и обобщение рисунка (цельность).

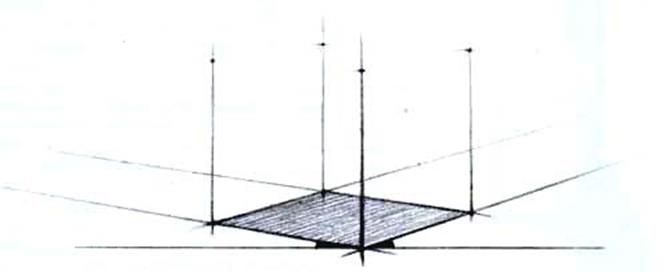
Рис. 38. Перспективное построение куба

Рисование призмы

Продолжая рассматривать принципы построения конструкции объемных тел, необходимо ознакомиться с изображением геометрических форм гранных предметов (трехгранная и шестигранная призмы).

Трехгранная призма характеризуется шестью точками пространственных углов оснований и тремя линиями ребер. Ось призмы определяется линиями, проведенными от пространственных углов оснований перпендикулярно к ее противоположным сторонам. Из точек их пересечения проводят вертикальную линию, которая и будет осью призмы. При построении трехгранной призмы необходимо правильно выбрать точку зрения. Предмет должен быть изображен таким образом, чтобы он выглядел трехмерным, с двумя видимыми плоскостями и передним ребром, несколько смещенным в сторону. Трехгранная призма при таком повороте будет наиболее выразительна, объемна и целесообразна при условии, что предмет расположен в оптимальном перспективном ракурсе.

Большие трудности испытывают студенты при определении величин отрезков граней в перспективном ракурсе на основании призмы. Чтобы избежать ошибок, рекомендуется использовать дополнительную окружность (в плане, вид сверху), на которой, в соответствии с видимым положением предмета, точно определяются пространственные углы основания призмы. Таким образом, для правильного изображения призматических форм необходимо построить цилиндрическую схему с последующим построением в ней гранных форм.

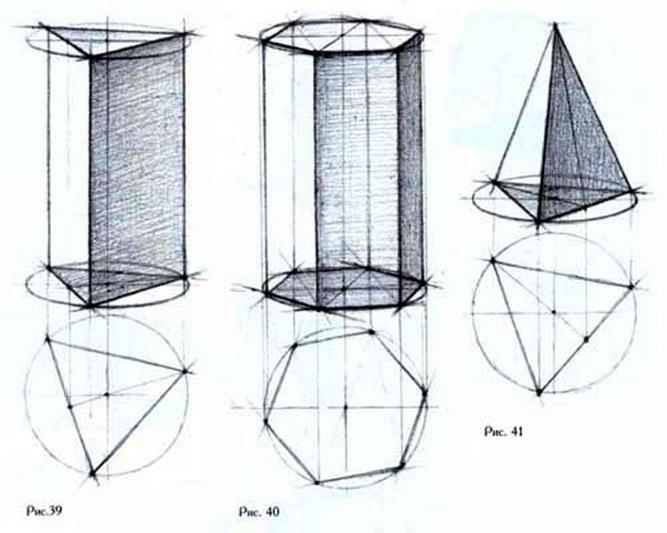
Рис. 39-41

Построение трехгранной призмы следует начинать с проведения горизонтальной линии (она должна быть проведена строго горизонтально). Это дает возможность правильно определить положение поверхности оснований призмы по отношению к оси тела. После чего следует провести вертикальную осевую линию. Отмечая радиус основания, нарисовать окружность (эллипс) в перспективном ракурсе (рис.39). Для правильного определения пространственных точек углов основания на эллипсе необходимо над ним, в соответствии с радиусом эллипса, по одной оси нарисовать круг. Рисуя его, проверить, насколько правильно он нарисован, так как на искаженном круге невозможно будет точно определить пространственные точки и величины отрезков граней. От того, как верно они определены на круге, во многом будет зависеть правильность изображения поверхности основания призмы и всего предмета в целом.

Точно определив на круге видимое положение точек пространственных углов основания призмы, перенесите их на эллипс. Для определения ее верхнего, основания следует повторить рисунок эллипса, после чего, соединяя вертикальными линиями ребер пространственные точки оснований, получают построение изображения трехгранной призмы. На перспективном изображении призмы окружность (эллипс) нижнего основания должна быть несколько шире верхней.

Производя построение предмета на плоскости, следует строго соблюдать пропорции и перспективу. Для большей выразительности ее объемно-пространственной характеристики следует выделить ближние края формы более контрастными линиями, ослабляя и смягчая их по мере удаления. Во время продолжительного, многочасового занятия рисунком можно постепенно избавиться от всех вспомогательных линий. Рисунок в процессе построения следует выполнять легким нажимом карандаша на бумагу, с тем, чтобы по мере уточнения изображения можно было корректировать и удалять ненужное.

Шестигранная призма характеризуется двенадцатью точками пространственных углов основания и шестью линиями ребер. Ее ось определяется линиями, проведенными от противоположных пространственных углов основания, где точка их пересечения будет центром, через который проходит ось призмы. Для правильного определения ее пространственных углов, так же, как и при построении трехгранной призмы, необходимо начинать работу с построения эллипса и окружности под ним. В соответствии с видимым положением предмета при данной точке зрения следует правильно определить на окружности точки пространственных углов правильного шестигранника. Необходимо обратить внимание на поворот призмы, не следует рисовать шестигранную призму при симметричном расположении ее плоскостей. Поэтому при выборе места рисования нужно сесть так, чтобы предмет выглядел наиболее выразительно, объемно, как, например, показано на рис.40.

Перспективное построение шестигранной призмы производят тем же способом, как и при изображении трехгранной призмы. Сложность состоит в правильном определении с видимого положения перспективно сокращенных граней, их пропорциональных отношений. В этом случае также следует пользоваться вспомогательной окружностью в плане у нижнего основания призмы, как показано на рис.40. Построив окружность основания призмы, нужно определить шесть пространственных углов по окружности. При этом важно правильно отложить равные отрезки с учетом поворота призмы, т.е. с видимого положения. Соединяя точки легкими линиями, необходимо проследить за параллельностью противоположных сторон. Получив точки пространственных углов основания, так же, как и в первом случае, следует перенести их на нижнее основание эллипса. Необходимо отметить, что при переносе пространственных углов на основание эллипса учитывают перспективное сокращение его дальней половины, хотя эти изменения и несущественны. Главное, не допустить обратной перспективы.

Соединив линиями все точки на основаниях, приступают к проверке выполненных работ. Замеченные ошибки, не откладывая, исправляют. В целях достижения наибольшей выразительности изображения пространственной формы нужно ближние вертикальные и горизонтальные линии ребер усилить, а дальние - ослабить. При необходимости продолжения работы над рисунком следует избавиться от вспомогательных линий построения при помощи ластика.

Трехгранная пирамида (рис.41) характеризуется тремя точками пространственных углов основания, точкой вершины и шестью линиями ребер.

Для правильного изображения пирамиды рисунок следует начинать с построения ее основания, что аналогично построению призматической формы. Соединив точки пространственных углов основания линиями, необходимо найти конструктивную ось пирамиды и точку ее вершины.

Положение конструктивной оси определяется линиями, проведенными от пространственных углов основания перпендикулярно к его сторонам. От точки пересечения проводят вертикальную линию. Затем необходимо определить положение точки вершины пирамиды на осевой линии, что осуществляется в соответствии с пропорциональной величиной высоты натурной модели. После чего следует соединить вершину с пространственными углами основания.

Рис. 42-43

Четырехгранная пирамида (рис.42), в отличие от трехгранной, характеризуется четырьмя точками пространственных углов основания, точкой вершины и восемью линиями ребер. Конструктивная ось пирамиды, аналогично трехгранной, определяется соединением линиями их противоположных пространственных углов. Из точки пересечения проводят вертикальную (осевую) линию, на которой должна быть обозначена точка вершины пирамиды.

При построении пирамиды в горизонтальном положении следует обратить внимание на положение оси пирамиды по отношению к центру ее основания (рис. 43). При этом плоскость основания пирамиды по отношению к ее конструктивной оси должна находиться строго под прямым углом, то есть перпендикулярно, независимо от положения предмета при данной точке зрения. Структура строения тела также остается неизменной.

Рисование тел вращения

Тела вращения характеризуются осью, радиусами оснований и конструктивными точками образующей поверхности тел. Чтобы лучше разобраться в принципах конструктивного построения формы цилиндра и конуса, следует обратить внимание на рис. 44, где они изображены в виде прозрачных проволочных моделей. На рисунках ясно выражены конструктивная основа и объемно-пространственная характеристика формы предметов. Задача состоит в том, чтобы научиться грамотно и правильно изображать их на плоскости. Для этого необходимо усвоить основные принципы и способы конструктивного построения таких изображений.

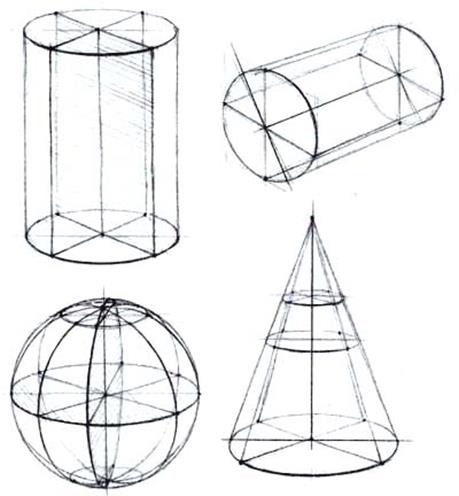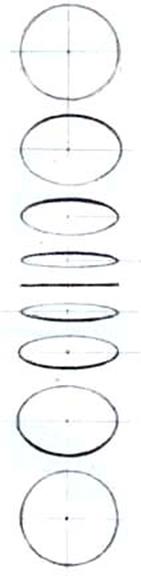Рис.44	Рис.45

Прежде чем перейти к построению тел вращения необходимо обратить внимание на одно обстоятельство. В изображении тел вращения одним из наиболее сложных элементов является рисование окружностей их оснований в перспективе. Для наглядности приведен рис.46, где показаны типичные ошибки, допускаемые студентами при рисовании оснований цилиндров. Так, основание первого представляет собой фигуру из двух дуг, образующих при пересечении острые углы по краям, из-за чего отсутствует впечатление круга в ракурсе. Во избежание подобных ошибок, попробуем выполнить следующую работу. Вырежем из картона круг, вставим по его краям симметрично две кнопки с пластмассовой головкой. Затем, держа большим и указательным пальцами головки кнопок, рассмотрим круг в разных наклонных положениях. Вращая его вдоль оси, мы увидим, как окружность изменяет форму, превращаясь из круга в более узкую фигуру. Но как бы мы ни поворачивали круг, он никогда не образует углов, а принимает форму замкнутой кривой с плавным изгибом очертаний боковых контуров. Для примера рассмотрим рисунок колец, расположенных в разном перспективном ракурсе (см. рис.45). В зависимости от положения колец в ракурсе, их форма постепенно изменяется. Чем выше линия горизонта, тем больше расширяется кольцо (круг, окружность) и, наоборот, по мере приближения к линии горизонта кольцо сужается, превращаясь постепенно в форму в виде прямой линии, когда линия горизонта (уровень глаза) окажется на одном уровне с кольцом.

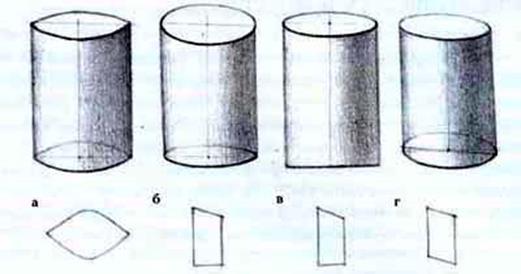Рис.46. Типичные ошибки, допускаемые при рисовании цилиндра: а - вид сверху; б,в,г, - вид слева	Рис.47

При низком расположении линии горизонта изменение форм колец происходит точно таким же образом, как и в первом случае. Особого внимания заслуживает положение кольца на уровне глаз наблюдателя, когда оно представляет собой прямую линию. В этом случае не только кольцо, но и любая горизонтальная плоскость будет видна как прямая линия, причем не только при горизонтальном, но и вертикальном, и наклонном их положении.

Рассмотрев и изучив окружности и их изменения в перспективном ракурсе, можно перейти к способам и приемам изображения окружностей на плоскости.

Окружность - это замкнутая геометрическая линия, все точки которой отстоят от центра на равном расстоянии.
Эллипс - это замкнутая кривая линия, которая строится на двух взаимно перпендикулярных осях: большой - горизонтальной и малой - вертикальной, делящих друг друга пополам в точке пересечения. В рисунке под эллипсом следует понимать перспективное изображение окружности, где нет углов, а есть плавный переход от ближней части к дальней.

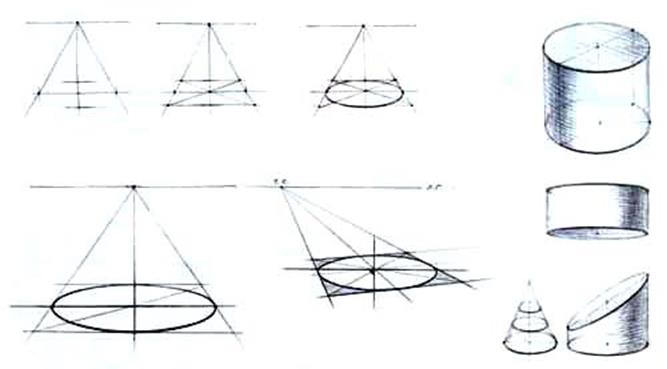
Рис.48

Для правильного перспективного построения эллипса необходимо рассмотреть способы и приемы изображения квадрата с окружностью на плоскости, используя для этого перспективно лежащий квадрат и его диагонали, на которых отмечаются дополнительные точки (рис.48). Построение эллипса есть начальный этап работы над построением цилиндра и других тел вращения в вертикальном положении на горизонтальной плоскости. В качестве примера перспективного построения окружности возьмем предмет, форма которого есть окружность, - спортивный обруч. Для оптимального рассмотрения предмета в ракурсе обруч положим на пол на расстоянии 6-7 метров. Изображение следует начинать с определения линии горизонта и точки схода на ней. В этом случае точка схода окружности обруча будет находиться на уровне вашего глаза (линия горизонта). Определив линию горизонта, пометьте на ней точку схода, а от нее проведите перпендикулярную линию, на которой нужно отметить центр окружности обруча. Через эту точку следует провести горизонтальную линию, параллельную линии горизонта, отложить на ней вправо и влево радиусы обруча, а полученные точки соединить с точкой схода. Имея линии схода с учетом перспективных сокращений, приступайте к определению на глаз длины малой оси эллипса.

Постройте квадрат в перспективе таким образом, чтобы его стороны проходили через полученные засечки. Для этого нужно обвести уже намеченные вспомогательные линии, уходящие в глубину точки схода. Правильной прорисовке окружности способствует определение ее центра, для чего соединяют двумя диагональными линиями противоположные пространственные углы квадрата. Их пересечение даст центр окружности, через который по горизонтали проходит большая ось эллипса. Причем, большая ось эллипса на горизонтальной плоскости всегда горизонтальна, ее длина соответствует горизонтальному диаметру окружности. Его малая ось определяет вертикальную ширину эллипса и находится под прямым углом к большой оси.

Следует уточнить, что при пересечении двух диагоналей точка пересечения должна лежать на вертикальной линии, а не в стороне. Определяя большую ось эллипса, намечайте точки на пересечении с линиями, уходящими в точку схода, а также точки, находящиеся вдоль средней линии - на пересечении с горизонтальными сторонами квадрата, так как эти точки будут основой для правильной прорисовки окружности в квадрате. Вместе с тем, они необходимы для определения точек касания окружностей со сторонами квадрата. Правильно определив их, приступайте к прорисовке окружности (эллипса). По мере ее завершения следует усилить ближнюю часть, а дальнюю - ослабить. Это придает рисунку впечатление пространственности формы.

Как показывает педагогическая практика, большую трудность для студентов представляет построение окружности (эллипса) в квадрате, особенно при изображении архитектурных деталей (капителей) и других сложных форм, связанных с сочетанием цилиндрических тел с квадратными. Так, например, производя построение капители дорического ордера, вписывая окружность в ромб квадратной абаки, зачастую неверно определяют ее горизонтальное положение - большую ось эллипса, что ведет к искажению изображения окружности эллипса и рисунка в целом. Независимо от положения углов ромба капители, эллипс, как уже упоминалось выше, должен находиться всегда в горизонтальном положении. Поэтому в целях упрощения рекомендуется начинать построение подобных предметов с правильного построения эллипса окружности. Построив окружность с учетом видимого положения и ракурса, следует построить на ее основе элемент абаки. Более подробно об этом будет сказано ниже.

Перспективное построение окружностей подводит студентов к правильному изображению предметов, относящихся к телам вращения. Так, например, упражнения по рисованию цилиндра помогут в дальнейшем при изображении сложных по форме предметов, в которых окружность является важным составным элементом. Соблюдая методический принцип последовательности выполнения учебных задач, следует перейти от построения окружностей к построению изображения цилиндра и конуса.

Рисование цилиндра

Цилиндр - геометрическое тело, форма которого состоит из трех поверхностей: двух одинаковых по форме плоских кругов и одной, образующей форму, цилиндрической поверхности. Для того чтобы лучше разобраться и понять конструктивную основу строения формы цилиндра, в качестве наглядного пособия рассмотрим его каркасную модель. Изготовить такую модель-каркас не составляет труда. Для этого можно использовать проволоку - алюминиевую, медную, стальную или из мягкого сплава. Длина большой стороны каркаса может быть в пределах 7-10 см.

Изучение в рисунке каркасных моделей позволяет студентам лучше освоить конструктивную сущность предмета, его взаимосвязь и пространственность формы.

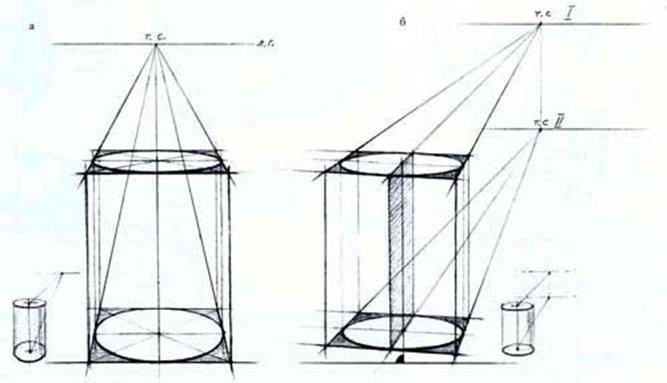
Рис.49. Перспективное построение окружностей оснований цилиндра: а - с одной точкой схода; б - с двумя точками схода

Изображение геометрического тела, расположенного на горизонтальной плоскости в обычном вертикальном положении, следует начинать с построения его основания. Как видно, на основаниях цилиндра имеются круглые по форме поверхности, ограниченные окружностью. С окружностью мы уже ознакомились и знаем методы и способы ее построения на плоскости. Основываясь на методе линейно-конструктивного построения изображения каркасных моделей, следует перейти к рассмотрению изображения цилиндра.

Изображение цилиндра следует начинать с определения основных пропорциональных величин - диаметра оснований и высоты.

Построение плоскостей кругов оснований производят тем же способом, что и при изображении окружностей - вписыванием в квадрат (рис.48).

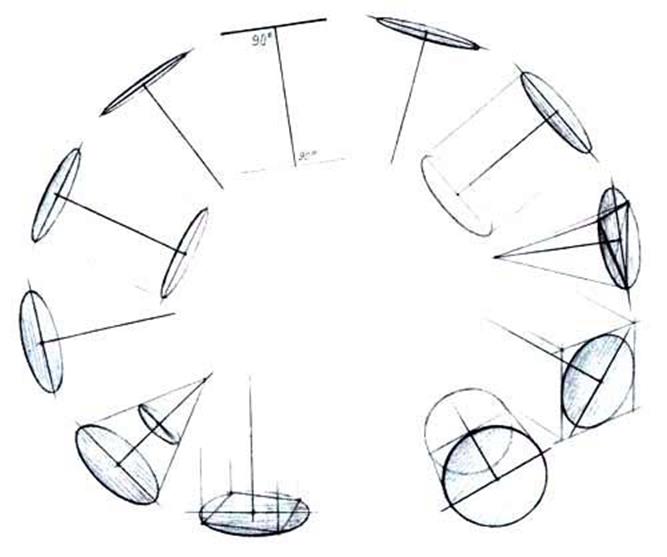
Рис.50

Ось вращения тела (ось цилиндра) всегда перпендикулярна к плоскостям кругов основания. При прорисовывании окружности в квадратах их вертикальные и горизонтальные оси попадают своими концами в середины сторон квадрата, т.е. в точки касания окружности со сторонами поверхности цилиндра (рис.48,49).

Рассматривая форму каркаса цилиндра, видим, что нижнее основание шире верхнего, следовательно, ближняя высота поверхности цилиндра больше, чем дальняя. Их различия обусловлены перспективной закономерностью. При этом необходимо заметить, что чрезмерно широкое нижнее основание цилиндра не способствует правильному и убедительному построению рисунка цилиндра. Поэтому ширина нижнего эллипса относительно верхнего должна быть чуть больше, равно как при наблюдении цилиндра с дальней точки зрения, а не с ближней.

При изображении окружностей оснований эллипса на гипсовом цилиндре его нижнее основание следует прорисовывать насквозь, т.е. видимым, с последующим его удалением для продолжения работы с помощью светотеней. Это даст возможность проследить за различиями в размерах оснований.

Завершив перспективное построение окружностей оснований цилиндра, приступайте к прорисовке краев формы образующей поверхности, соединяющей оба круга. При этом линии не должны быть чрезмерно контрастными, так как они находятся дальше, чем ближние поверхности цилиндра - ближние края эллипса и его изображающая поверхность. Однако без усиления линий ближних краев оснований получить в рисунке достаточное впечатление объемно-пространственной формы невозможно.

По окончании работы над построением рисунка цилиндра необходимо приступить к его проверке. Проверять следует, отходя от своего места на расстояние не менее 2-4 м, в зависимости от размера рисунка. Чем больше его размер, тем с большего расстояния его следует рассматривать.

Внимательно проверив допущенные в процессе работы ошибки, их следует, не откладывая, исправить.

Изображение цилиндра в горизонтальном положении имеет свои особенности в отличие от построения цилиндра в вертикальном положении. Это обусловлено его цилиндрической образующей поверхностью, связывающей между собой оба круглых основания цилиндра. Для примера рассмотрим каркас цилиндра (рис.52).

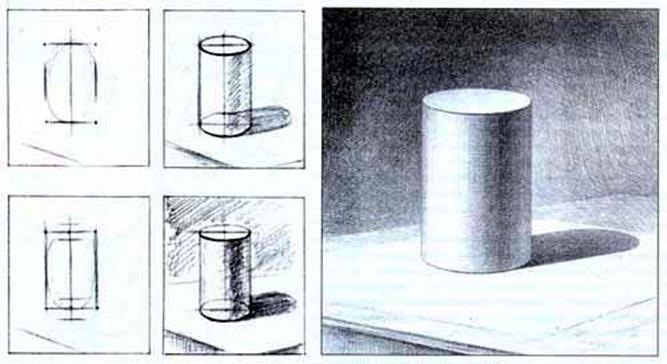
Рис.51. Последовательность рисования цилиндра

Цилиндр в горизонтальном положении можно строить на основе прямоугольной призмы. Это облегчает объемно-пространственное и конструктивное построение цилиндра, позволяет правильно определить ось вращения по отношению к оси эллипса и, следовательно, правильно строить окружности оснований (эллипсы). Определив линию горизонта и положение предмета в пространстве относительно угла зрения (в этом случае цилиндр находится несколько сбоку, а точка зрения выше цилиндра), нужно наметить его местоположение. При построении очень важно правильно определить углы горизонтальных направлений предмета на плоскости, поэтому изображение призмы начинают с построения ее основания, у которого все стороны попарно равны высоте цилиндра и диаметру оснований окружностей. В последующем эта призма будет служить каркасом для построения цилиндра в горизонтальном положении.

Построение призмы производят с ближайших к нам точек на пересечении сторон параллелепипеда. В соответствии с положением предмета нужно наметить горизонтальную, уходящую по направлению к точкам схода линию основания сторон призмы. Направления этих двух основных линий, идущих к точкам схода, должны определять основу для правильного построения призмы, а затем - цилиндра. После чего производят построение с учетом перспективы. Для определения точек осевой линии призмы следует провести диагонали противоположных углов ее передней грани. Точка пересечения диагоналей будет центром оси призмы и цилиндра. Чтобы правильно вписать окружность основания цилиндра (эллипс) в переднюю грань призмы, необходимо точно определить прямой угол межд