Нивелирование поверхности по квадратам
Нивелирование поверхности производят для получения топографического плана местности в крупных масштабах, а также для выполнения вертикальной планировки площадок. В зависимости от характера рельефа местности нивелирование поверхности может быть выполнено или путем нивелирования вершин построенной на местности сетки квадратов, или проложением теодолитных и нивелирных магистральных ходов с поперечниками.
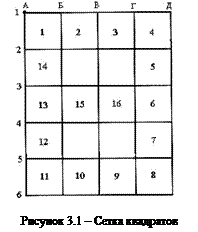 Обычно нивелирование поверхности по квадратам применяют для равнинной местности, а нивелирование по магистралям с поперечниками используют при пересеченной местности с значительными углами наклона. Наиболее распространенным способом нивелирования поверхности является н и в е л и р о в а н и е п о к в а д р а -т а м. В этом способе на участке местности, намеченном под строительство, разбивают сетку квадратов. Длины сторон квадратов обычно берут от 20 до 200 м с таким расчетом, чтобы они на плане были равны 2–6 см. Вершины квадратов закрепляют точкой и сторожком. На сторожке подписывают номер вершины квадрата, состоящий из обозначения двух линий, пересечение которых образует точку, например 1А, 2А, …, 1Б, 2Б и т. д. (рисунок 3.1).
Обычно нивелирование поверхности по квадратам применяют для равнинной местности, а нивелирование по магистралям с поперечниками используют при пересеченной местности с значительными углами наклона. Наиболее распространенным способом нивелирования поверхности является н и в е л и р о в а н и е п о к в а д р а -т а м. В этом способе на участке местности, намеченном под строительство, разбивают сетку квадратов. Длины сторон квадратов обычно берут от 20 до 200 м с таким расчетом, чтобы они на плане были равны 2–6 см. Вершины квадратов закрепляют точкой и сторожком. На сторожке подписывают номер вершины квадрата, состоящий из обозначения двух линий, пересечение которых образует точку, например 1А, 2А, …, 1Б, 2Б и т. д. (рисунок 3.1).
Сетку квадратов строят на местности при помощи теодолита и мерной ленты. Вначале разбивают наружный полигон 1А, 1Д, 6Б, 6А, для чего в одной из вершин полигона, например 1А, устанавливают теодолит. Выбирают и закрепляют вехой исходное направление (например, 1А – 1Д), и от него под углом 90о строят направление 1А – 6А, по которому устанавливают веху. По полученным направлениям мерной лентой или рулеткой откладывают стороны квадратов заданной длины и закрепляют их колышками. Затем теодолит переносят в точку 6А, откладывают от линии 6А – 1А прямой угол и устанавливают веху по направлению 6А – 6Д, вдоль которого отмеряют длины сторон квадратов. Для контроля разбивки производят измерение последней линии 1Д – 6Д, длина которой должна отличаться от теоретической не более чем на 1:1000 от периметра полигона. При соблюдении указанного допуска закрепляют вершины квадратов по линии 1Д – 6Д. Вершины квадратов, которые находятся внутри
полигона (2Б, 2В, 3Б и т. д.), находят и закрепляют на пересечении створов, выполняя промеры с вехи на веху. Например, с 2А на 2Д, с 3Д на 3А и т. д.
Одновременно с разбивкой сетки квадратов ведут съемку контуров ситуации и предметов местности, привязывая их к вершинам квадратов. При наличии резких изменений уклонов на сторонах квадратов дополнительно закрепляют плюсовые точки, измеряя до них расстояния от ближайших вершин. Все данные съемки заносят в абрис, в котором также показывают стрелками диагонали квадратов с неизменным уклоном местности.
Для определения высот вершин квадратов производят их нивелирование, которое выполняют или из середины каждого квадрата, или с нескольких станций с общими связующими точками.
 При нивелировании из середины каждого квадрата устанавливают нивелир примерно в центре первого квадрата и берут отсчеты по черной стороне рейки, установленной на всех его вершинах. Потом аналогично нивелируют второй квадрат. Запись отсчетов ведут на схематическом чертеже (рисунок 3.2). Для контроля нивелирования во втором квадрате вычисляют разности отсчетов по рейке на точках у стороны, смежной для обоих квадратов.
При нивелировании из середины каждого квадрата устанавливают нивелир примерно в центре первого квадрата и берут отсчеты по черной стороне рейки, установленной на всех его вершинах. Потом аналогично нивелируют второй квадрат. Запись отсчетов ведут на схематическом чертеже (рисунок 3.2). Для контроля нивелирования во втором квадрате вычисляют разности отсчетов по рейке на точках у стороны, смежной для обоих квадратов.
Это будут разности горизонтов нивелира на станциях в соседних квадратах. Расхождения между двумя значениями разностей допускается не более ± 6 мм. Например, на рисунке 3.2 у точки 1Б разность равна 2226 – 1306 = +920 мм, а у точки 2Б – соответственно 1074 – 152 = +922 мм. Если разности отсчетов на двух вершинах смежной стороны квадратов в допуске, то вычисляют среднюю разность горизонтов нивелира на двух станциях. Например, у общей стороны 1-го и 2-го квадратов средняя разность составит (+920 + 922)/2 = +921 мм, которую записывают в середине у смежной стороны (см. рисунок 3.2).
Затем переходят с нивелиром в центр третьего квадрата и аналогично находят разности горизонтов нивелира между третьим и вторым квадратами и т. д. Последовательность нивелирования квадратов показана на рисунке 3.1 порядковыми номерами. После нивелирования всех указанных квадратов подсчитывают сумму средних разностей по внешнему кольцу квадратов (1–14). Это будет невязка по замкнутому ходу. Она должна быть меньше величины
± 6 мм ∙  ,
,
где n – число средних разностей.
Если невязка не более допустимой величины, то ее распределяют с обратным знаком поровну на все разности, и полученные поправки записывают над средними разностями. Затем по данным привязки к близлежащему реперу определяют высоту одной из вершин квадратов. Прибавляя к этой высоте отсчет по рейке на данной точке, получают горизонт нивелира на станции, с которой был взят отсчет по рейке. На рисунке 3.2 высота точки 1А из данных привязки равна 40,705 м. Тогда горизонт нивелира в первом квадрате будет равен 40,705 + 1,152 = 41,857 м. Он записан под номером станции. Последовательно прибавляя к предыдущим горизонтам нивелира исправленные поправками средние разности (уравненные разности), получают горизонты нивелира на всех станциях внешнего контура квадратов. Например, горизонт нивелира во втором квадрате будет 41,857 + 0,920 = 42,777 м и т. д.
В конце вычислений необходимо точно получить горизонт нивелира в первом квадрате, что является контролем правильности вычислений. Для этого к горизонту нивелира в 14-м квадрате прибавляют последнюю разность. Далее определяют невязку для внутреннего хода, проходящего от 6-й через 16-ю и 15-ю к 13-й станции (см. рисунок 3.1). Для этого от суммы средних разностей по внутреннему ходу вычитают разность горизонтов нивелира 13-го и 6-го квадратов. Если эта невязка допустима, то ее, аналогично замкнутому ходу, распределяют по внутреннему ходу и вычисляют уравненные горизонты нивелира в 16-м и 15-м квадратах. При этом вычисления горизонтов нивелира начинают с 6-го квадрата, а заканчивают контрольным получением горизонта нивелира в 13-м квадрате.
Затем определяют высоты вершин квадратов как разность горизонта нивелира и отсчетов по рейке, взятых с данной станции. Например, высота вершины 1Б равна 41,857 – 1,306 = 40,551 м. Высоту этой же вершины для контроля можно получить через горизонт нивелира второго квадрата, а именно: 42,777 – 2,226 = 40,551 м. При этом допускается расхождение между полученными высотами до ± 3 мм. На рисунке 3.2 вычисленные высоты подчеркнуты у соответствующих вершин.
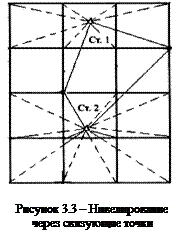
Если длины сторон квадратов небольшие, то их нивелирование можно выполнять с нескольких станций с общими связующими точками. Схема такого нивелирования показана на рисунке 3.3. Каждая станция 1, 2, 3 имеет связь с соседней через 2-3 связующие точки, показанные на рисунке черными точками. Направления на промежуточные вершины квадратов изображены пунктирными линиями. При нивелировании запись отсчетов по рейкам в этом случае ведут в обычном журнале.
Вычисление разности горизонтов нивелира по отсчетам на связующих точках, уравнивание этих разностей (при образовании замкнутого или разомкнутого хода), вычисление значений горизонтов нивелиров и по ним высот вершин квадратов производят аналогично тому, как это выполнялось при нивелировании из середины каждого квадрата.
 При составлении плана нивелирования поверхности вначале на листе чертежной бумаги в заданном масштабе строят сетку квадратов, используя для этого дирекционный угол начальной линии и длины сторон квадратов. Затем по данным абриса съемки наносят ситуацию и предметы местности. Около каждой вершины квадрата выписывают их высоты, округляя до сотых долей метра. Далее при помощи прозрачной бумаги (кальки или восковки) по всем сторонам квадратов и по одной из диагоналей в каждом квадрате с наибольшим постоянным уклоном выполняют интерполирование горизонталей, находя точки пересечения горизонталями сторон квадратов. Соединяя точки с одноименными высотами плавными кривыми линиями, проводят горизонтали, которые оформляют светло-коричневым цветом толщиной 0,2 мм. Горизонтали кратные 0 и 5 м проводят толще в 2 раза с указанием их высоты.
При составлении плана нивелирования поверхности вначале на листе чертежной бумаги в заданном масштабе строят сетку квадратов, используя для этого дирекционный угол начальной линии и длины сторон квадратов. Затем по данным абриса съемки наносят ситуацию и предметы местности. Около каждой вершины квадрата выписывают их высоты, округляя до сотых долей метра. Далее при помощи прозрачной бумаги (кальки или восковки) по всем сторонам квадратов и по одной из диагоналей в каждом квадрате с наибольшим постоянным уклоном выполняют интерполирование горизонталей, находя точки пересечения горизонталями сторон квадратов. Соединяя точки с одноименными высотами плавными кривыми линиями, проводят горизонтали, которые оформляют светло-коричневым цветом толщиной 0,2 мм. Горизонтали кратные 0 и 5 м проводят толще в 2 раза с указанием их высоты.
План вычерчивают в условных топографических знаках и оформляют в соответствие с приведенным в методических указаниях для выполнения лабораторных работ примером.
