Проверка правильности программ

Тести́рование програ́ммного обеспе́че́ния — процесс исследования, испытания программного продукта, имеющий две различные цели:

· продемонстрировать разработчикам и заказчикам, что программа соответствует требованиям;

· выявить ситуации, в которых поведение программы является неправильным, нежелательным или не соответствующим спецификации^[1].

По объекту тестирования

· Функциональное тестирование

· Тестирование производительности

· Нагрузочное тестирование

· Стресс-тестирование

· Тестирование стабильности

· Конфигурационное тестирование

· Юзабилити-тестирование

· Тестирование интерфейса пользователя

· Тестирование безопасности

· Тестирование локализации

· Тестирование совместимости

По знанию системы

· Тестирование чёрного ящика

· Тестирование белого ящика

· Тестирование серого ящика

По степени автоматизации

· Ручное тестирование

· Автоматизированное тестирование

· Полуавтоматизированное тестирование

По степени изолированности компонентов

· Модульное тестирование

· Интеграционное тестирование

· Системное тестирование

По времени проведения тестирования^{[источник не указан 196 дней]}

· Альфа-тестирование

· Дымовое тестирование (англ. smoke testing)

· Тестирование новой функции (new feature testing)

· Подтверждающее тестирование

· Регрессионное тестирование

· Приёмочное тестирование

· Бета-тестирование

По признаку позитивности сценариев

· Позитивное тестирование

· Негативное тестирование

По степени подготовленности к тестированию

· Тестирование по документации (формальное тестирование)

· Интуитивное тестирование (англ. ad hoc testing)

Теория графов и мографов

Понятие графов

Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.
Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.
Если ребра не имеют ориентации, граф называется неориентированным.

Граф

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра - линиями, соединяющими точки (рис. 2.15).

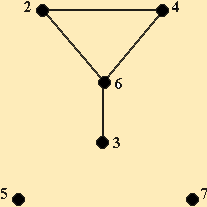
Рис. 2.15

Петля это дуга, начальная и конечная вершина которой совпадают.

Простой граф граф без кратных ребер и петель.

Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.

Виды графов

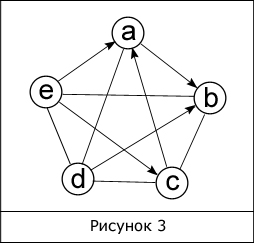
Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называетсяориентированным или орграфом (рис. 2).

В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

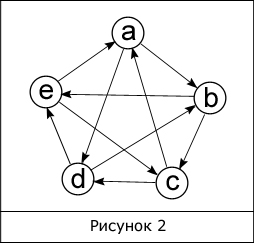
В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.

Ориентированные графы имеют следующую форму записи:

G=(V, A), где V – вершины, A – направленные ребра.

Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.