Графическая форма представления алгоритма

Графическая форма представления называется блок-схема,в которой для представления отдельных блоков алгоритма используется обусловленный набор геометрических фигур. Графическая форма предназначена только для человека и главное достоинство – наглядность; блок-схема позволяет охватить весь алгоритм сразу, отследить различные варианты его выполнения. По блок-схеме гораздо проще осуществляется запись алгоритма на каком-либо формальном языке. Графическое представление конструкций формального языка (условные операторы, циклические операторы и т.д.) осуществляется посредствам синтаксических диаграмм.

Структурная теорема

После того, как были рассмотрены возможные способы записи алгоритмов, вполне закономерным представляется вопрос о технологии их разработки. До середины 60-х годов теории разработки алгоритмов не существовало - процесс разработки целиком определялся опытом и искусством программиста. Однако по мере роста сложности программ возникла необходимость создания методологии их разработки, и она появилась в виде структурного программирования. Идеи структурного программирования были высказаны в 1965 г. Э. Дейкстрой, но сведены в некую законченную систему правил они не были. В том же году итальянские математики К. Бом и Д. Джакопини сформулировали теорему о структурности. Прежде, чем рассмотреть ее суть, необходимо ввести некоторые понятия.

Поскольку алгоритм определяет порядок обработки информации, он должен содержать, с одной стороны, действия по обработке, а с другой стороны, порядок их следования, называемым потоком управления.

Рассмотренные выше блоки, связанные с обработкой данных, делятся на простые и условные. Особенность простого действия в том, что оно имеет один вход и один выход, в отличии от условного, обладающим двумя выходами в зависимости от того, истинным ли окажется условие. Простое действие не означает, что оно единственное - это может быть некоторая последовательность действий.

Часть алгоритма, организованная как простое действие, т.е. имеющая один вход (выполнение начинается всегда с одного и того же действия) и один выход (т.е. после завершения данного блока всегда начинает выполняться одно и то же действие), называется функциональным блоком.

Из этого определения, в частности, следует, что каждое простое действие является функциональным блоком, а условное - нет.

Согласно положениям структурного программирования можно выделить всего три различных варианта организации потока управления действиями алгоритма. Поток управления может обладать следующими свойствами:

1) каждый блок выполняется не более одного раза;

2) выполняется каждый блок.

Поток управления, в котором выполняются оба эти свойства, называется линейным - в нем несколько функциональных блоков выполняются последовательно. Линейному потоку на языке блок-схем соответствует структура:

Очевидно несколько блоков, связанных линейным потоком управления, могут быть объединены в один функциональный блок:

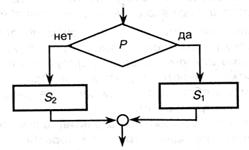
Второй тип потока управления называется ветвлением - он организует выполнение одного из двух функциональных блоков в зависимости от значения проверяемого логического условия. Блок-схема структуры:

Понятие структурный подход. Для разработки алгоритма сложных задач используется принцип структурного проектирования алгоритмов.
Структурный подход к созданию алгоритмов - это метод разработки алгоритма, который обеспечивает легкость чтения алгоритма, простоту проверки правильности выполнения алгоритма, удобство его модификации.

Этот метод предусматривает:

• конструирования алгоритма с использованием трех базовых алгоритмических структур;
• использование метода пошаговой детализации, т.е. измельчение задачи на более простые задачи, затем измельчения этих задач на еще более простые составляющие и т. д. (разработка алгоритма «сверху вниз»);
• анализ алгоритма, т.е. контроль правильности каждой структуры алгоритма и взаимосвязей структур.
Преимуществом структурного подхода является его модульность. Модуль - это последовательность логически связанных команд, которая оформлена в виде отдельного алгоритма. Эти вспомогательные алгоритмы можно конструировать и анализировать отдельно и независимо, используя их затем в основном алгоритме или других вспомогательных алгоритмах.

Эффективность алгоритмов

Рекурсия и эффективность алгоритмов.Рекурсивное программирование дает нам общий подход к решению задач – разбиению их на аналогичные подзадачи меньшей размерности, либо на задачи, представляющие собой шаги в возможных направлениях ее решения. Так или иначе, рекурсивные вызовы образуют древовидную структуру, количество вершин в которой определяет эффективность алгоритма (выражаемую обычно через трудоемкость). Разница между различными типами алгоритмов состоит в способе получения подзадач, их размерности, способе соединения полученных результатов.

 рекурсивное или обычное разделение.Идея разделения восходит к технологическому приему - модульному программированию (3.6). В своем первоначальном варианте она предполагает разбиение на задачи различной природы. Нерекурсивное разделение позволяет достичь определенного эффекта за счет разбиения задачи на множество идентичных задач меньшей размерности с последующим объединением результата. Типичным примером здесь является сортировка однократным слиянием (4.6). Применение того же самого алгоритма рекурсивно к полученным подзадачам дает следующий класс алгоритмов – рекурсивное разделение. Как правило, независимость полученных подзадач подразумевает соответствующее разделение исходных данных задачи на непересекающиеся подмножества – этому и соответствует сам термин разделение.Эффективность (и трудоемкость) таких алгоритмов, зависит от затрат на само разделение и от пропорций разделяемых частей: лучшему случаю соответствует деление на равные части (логарифмические зависимость), худшему – выделение единственного элемента (линейные зависимости).

 жадные алгоритмы.Идеальным случаем можно считать алгоритм, способный «выбрать из нескольких зол» единственно правильное. В основе его так же лежит принцип разделения, но в каждой точке он имеет основание выбрать одну из подзадач. Обычно это делается на основании особенностей организации обрабатываемых данных или их избыточности. Типичный пример: двоичный поиск в упорядоченных данных (4.6). Основой жадных алгоритмов является всегда довольно спорное утверждение: движение «по линии наименьшего сопротивления» в каждой точке приведет к желаемому результату.

 полный перебор (исчерпывающий, комбинаторный перебор). Перечисленные выше подходы основаны на всевозможных «ухищрениях», основанных на особенностях предметной области алгоритма. Если же ничего не помогает, то остается полный перебор всех возможных вариантов решения задачи (8.4).

 динамическое программирование.В процессе порождения дерева рекурсивных вызовов возможно повторение подзадач с одними и теми же данными. Если запоминать результат их выполнения, то эффективность алгоритма может быть значительно увеличена.