Аналого-цифровые преобразователи

2.1. Алгоритм аналого-цифрового преобразования

Алгоритм аналого-цифрового преобразования включает в себя следующие этапы:

– выборка значений исходной аналоговой величины в некоторые дискретные моменты времени, т.е. дискретизация сигнала по времени;

– округление полученной в некоторые моменты времени последовательности значений исходной аналоговой величины до некоторых известных величин, т.е. квантование сигнала по уровню;

– замена найденных квантованных значений некоторыми числовыми кодами, т.е. кодирование сигнала.

Процесс преобразования аналогового сигнала в цифровой представлен на рисунке 2.1.

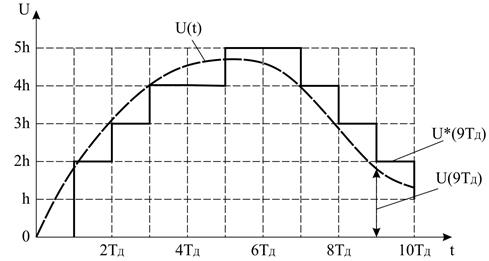
Рисунок 2.1 – Преобразование аналогового сигнала в цифровой

Здесь задана аналоговая последовательность U(t). Для получения ее дискретного эквивалента, необходимо выбрать отдельные ее значения через промежутки времени Т_Д. Величина Т_Д называется периодом дискретизации, соответственно процесс замены исходной аналоговой функции U(t)дискретной функцией U(nT_Д) – дискретизацией.

Полученная функция по-прежнему носит аналоговый характер, так как может принимать бесконечное число различных значений.

Операция квантования по уровню дискретной функции U(nT_Д) заключается в отображении бесконечного множества ее значений на некоторое конечное множество значений U^*_n, называемых уровнями квантования.Для выполнения данной операции весь динамический диапазон изменения дискретной функции U(nT_Д) разбивают на некоторое заданное число уровней N и производят округление каждой величины U(nTД) до ближайшего уровня U^*_n. Разница между двумя соседними уровнями называется шагом квантования h.

Для выполнения последнего этапа преобразования необходимо выбрать код, который способен отражать не менее (N+1)-го значений и каждому дискретному значению U^*_n сопоставить некоторый код.

Анализируя данный алгоритм, можно заметить, что процесс преобразования сопряжен с потерей части информации об исходном сигнале при переходе от непрерывной функции к дискретной. Кроме того, процесс квантования сигнала вносит в преобразование некоторую погрешность ε_i, которая называется шумом квантования. Для устранения данных погрешностей необходимо повышать частоту дискретизации и разрядность АЦП.

Характеристики АЦП

Микросхемы АЦП, как и любые другие, характеризуются широким спектром различных параметров, начиная от диапазона рабочих температур и заканчивая размером микросхемы. Данные характеристики указываются в документации на конкретную микросхему и должны быть учтены при проектировании реальных устройств.

В каталогах микросхем производители обычно указывают следующие параметры:

– разрядность (4 – 31 бит);

– число выборок в секунду (до 3,6GSPS);

– число каналов (1 – 64) – число аналоговых входов;

– поддерживаемый интерфейс (SPI, I²C, LVDS);

– напряжение питания (униполярное/биполярное) и опорное напряжение (от нескольких до пары десятков вольт);

– диапазон входного сигнала;

– потребляемая мощность (до нескольких десятых долей микроватт);

– цена (самые дешевые АЦП могут стоить меньше доллара; цена микросхем, применяемых в военной и космической отраслях, может достигать нескольких тысяч долларов).

В таблице 2.1 приведены несколько примеров микросхем АЦП, предлагаемых различными производителями.

Архитектура АЦП

Аналого-цифровые преобразователи подразделяются на два больших класса [6]:

– работающие на частоте Найквиста (Nyquist-rate);

– с передискретизацией (oversampling).

Различия между данными подходами показаны на рисунке 2.2. Здесь спектр частот входного сигнала ограничен частотой f_B. Согласно теореме Найквиста-Шеннона (теореме Котельникова), для его восстановления с наперед заданной погрешностью, необходимо дискретизировать его с частотой f_s > 2·f_B (fs = 2·fB называется частотой Найквиста). Как видно из рисунка 2.2, с ростом частоты дискретизации увеличивается защита от наложения спектров, что снижает шум квантования. Частота передискретизации может в несколько десятков раз превышать частоту Найквиста.

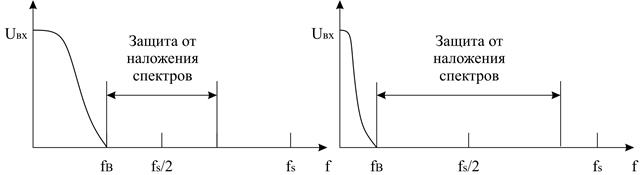
Рисунок 2.2 – Сравнение подходов к выбору частоты дискретизации

Таким образом, в АЦП первого класса алгоритм преобразования должен быть выполнен за один или несколько периодов дискретизации (цикл), в зависимости от спектра частот входного сигнала; АЦП второго класса позволяют затратить на преобразование несколько десятков циклов. Отсюда вытекает основное отличие между преобразователями: АЦП с передискретизацией обладают большей разрядностью, по сравнению с АЦП, работающими на частоте Найквиста; однако их быстродействие меньше. Типовые архитектуры АЦП рассмотрены ниже.

Таблица 2.1 – Параметры микросхем АЦП различных производителей [7 – 10]

Производитель	Наименование	Архитектура	Разрядность, бит	Число выборок, SPS	Число каналов	Поддерж. интерфейс	Цена,
Analog Devices	AD9484	Конвейерная		1G		Par	$36
AD7995	Послед. прибл.		140K		I2C/2-Wire	$1,8
AD6672	Конвейерная		250M		LVDS	$44,2
AD10465	Конвейерная		65M		Par	$754,46
AD7856	Послед. прибл.		285K		SPI	$10,2
AD7714	Сигма-дельта		1K		SPI	$8,38
Texas Instruments	TLC5510A	Флеш		20M		Par CMOS	$2,35
ADS7961	Послед. прибл.		1M		SPI	$2,25
THS1007	Конвейерная		6M		Par CMOS	$4,6
ADC12D1800			3,6G			$100
ADS5400-SP	Конвейерная		1G		LVDS, SPI	$9500,24
ADS8284	Послед. прибл.		1M		Par CMOS	$22
DDC264	Сигма-дельта		6,25K			$99
ADS1282	Сигма-дельта		4K		SPI	$34,5
MAXIM	MAX11642	Послед. прибл.		300K		SPI	$2,2
MAX11101	Послед. прибл.		200K		Micro wire, QSPI, SPI	$3,55
MAX1401	Сигма-дельта		4,8K		SPI	$14
MAX11202	Сигма-дельта		0,12K		SPI	$2,45
Linear Technology	LTC2288	Конвейерная		65M		Par CMOS
LTC2153-12	Конвейерная		310M		LVDS
LTC2497	Сигма-дельта				I2С
LTC2446	Сигма-дельта				PIS

2.3.1. Архитектура параллельного преобразования

Данная архитектура, называемая также full-flash, относится к преобразователям первого класса (рисунок 2.3).

N-разрядный АЦП такого типа содержит (2^N-1) компараторов и столько же источников опорного напряжения. На очередном цикле входное напряжение сохраняется схемой выборки и хранения, после чего происходит его сравнение со всеми опорными напряжениями. В результате с выходов компараторов снимается 2^N-1 – разрядный код, который преобразуется дешифратором в выходной код.

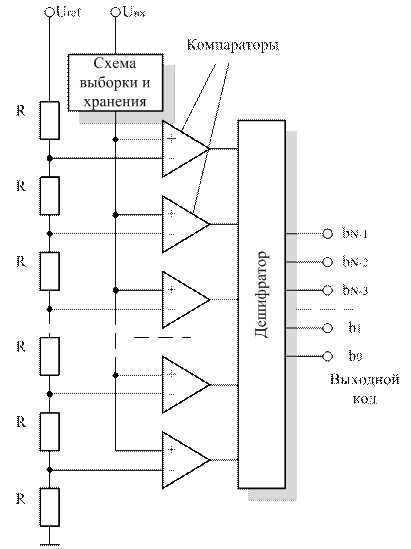
Рисунок 2.3 – Структурная схема АЦП параллельного преобразования

Реализация алгоритма преобразования в таком АЦП осуществляется за один цикл, поэтому такая архитектура позволяет достичь максимального быстродействия. Однако с увеличением разрядности число элементов схемы и, соответственно, площадь кристалла растут в геометрической прогрессии. Поэтому разрядность АЦП параллельного преобразования редко превышает восемь бит.

Конвейерная архитектура

Данная архитектура позволяет повысить разрядность full flash АЦП путем реализации алгоритма преобразования в несколько этапов (рисунок 2.4). Здесь входное напряжение сохраняется в схеме выборки и хранения, после чего M-битный АЦП производит грубую оценку входного сигнала (получение старших M битов). ЦАП затем преобразует цифровой код в аналоговый сигнал, который вычитается из входного сигнала. Остаток после усиления преобразуется в АЦП для получения младших N битов.

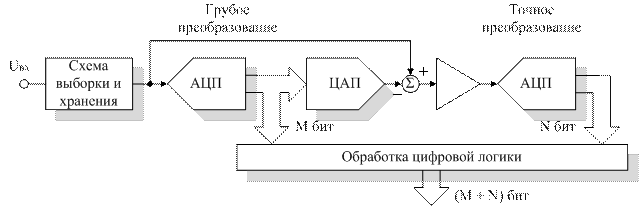
Рисунок 2.4 – Структурная схема конвейерного АЦП

При использовании восьмиразрядных АЦП параллельного преобразования, такой подход позволяет получить 16-битный АЦП. При этом число компараторов составляет 510. Реализация 16-битного АЦП параллельного преобразования потребовала бы 65536 компаратора. В общем случае можно использовать K АЦП, включенных в последовательность (рисунок 2.5). Время, затраченное на алгоритм преобразования, при этом составляет (K+1) циклов, включая цикл выборки входного напряжения.

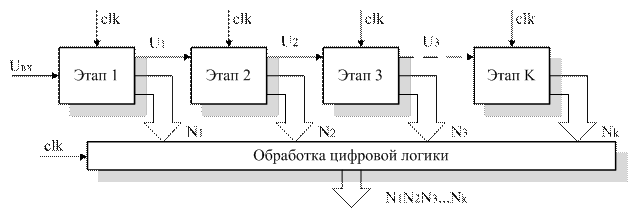
Рисунок 2.5 – K-этапная конвейерная архитектура

Бесконечное увеличение разрядности данной архитектуры ограничено сложностями согласования характеристик составных элементов. Каждое преобразование сигнала «аналоговый → цифровой → аналоговый» дает погрешность в вычислении остатка. С увеличением числа этапов, соответственно, растет погрешность.