Вурфные отношения русской матрицы
Соизмеримость различных пространственных предметов определяется путем сопоставления их со стандартным измерительным инструментом, т.е. в статике. При этом для каждого процесса существует определенный эталон. Таким эталоном для измерения длины служит, например, признанный всем миром метр или кратная ему часть — 1 см. А система его применения — евклидова геометрия. В результате таких измерений, как отмечал еще А.Л. Пилецкий [13], мы получаем двучастное членение измеряемого тела. Такое членение органически не связывает между собой элементы делимого тела.
И еще раз с удивлением отметим иное мышление составителей системы древнерусских саженей, в которой принципиально отсутствует единая для саженей стандартная измерительная единица, а сама система измерения не является евклидовой. На протяжении многих веков отсутствие единого стандарта не мешало, а более того — способствовало возведению великолепных эстетически пропорциональных природе сооружений еще и потому, что в древнерусской архитектуре все членения были трехчастными.
Почленные части трехчастного деления тела (вурфа) образуют систему взаимного пропорционирования и потому оказываютсянеразделимыми.
Надо отметить, что, например, в живой природе, в биологических телах, в строении тела человека трехчастное деление наблюдается постоянно. Приведу в подтверждение несколько отрывков из [13]:
«Пальцы рук и ног имеют трехфаланговое строение, руки — трехчленистое (плечо-предплечье-кисть), такое же ноги (бедро-голень-стопа); в масштабе размеров тела (в антропологии трехчленность также различают: верхний отрезок — от макушки головы до основания шеи; средний отрезок, или туловище, — от основания шеи до тазобедренного сочленения; нижний отрезок — от тазобедренного сочленения до конца пальцев ног).
Весьма показателен следующий факт: трехчленное устройство конечностей по данным эволюционной биологии появилось в живых организмах вместе с появлением самих скелетов, причем без каких-либо переходных форм (двучленной конечности, например, не существовало). Почленные части образуют! системы пропорций".
"Пропорция характеризует отношение длин двух элементов, а биологические тела, включая человека и произведения архитектуры, особенно древнерусской, простроены на трехчленных иерархиях. В итоге общая картина предстает в виде множества разнохарактерных и случайных отношений".
В.Петухов [14] исследовал изменение пропорциональных структур тела человека в процессе его роста по трехчастным блокам с использованием трехчленных "вурфных" пропорций (называемых двойным или ангармоническим отношением четырех точек) проективной и конформной геометрии:
"Для блока, состоящего из трех элементов с длинами а, b, с (можно эти три отрезка обозначить упомянутыми четырьмя точками), вурфное отношение W(а, b, с) вычисляется по формуле:
| W(a,b,с)=(а+b)(b+с)/b(a+b+с). | (9) |
При этом другой блок — с другими размерами и другими соотношениями элементов — а', b', с' будет ему конформно симметричен, если величины их вурфов будут равны, т.е. если:
W(a, b, с)=W(a', b',с').
Путем преобразований такие блоки могут быть совмещены один с другим с полным совпадением всех их точек ... В процессе роста размеры частей тела человека и их соотношения все время меняются. Эти изменения следуют принципам конформно-симметричных преобразований. Например, если взять соотношение стопы, голени и бедра в возрасте 1 года, 10 и 20 лет, то изменения выглядят так: 1:1,27:1,40; 1:1,34:1,55; 1:1,39:1,68.
Рост различных частей тела не протекает равномерно. Голень V и бедро увеличиваются значительно больше, нежели стопа, в результате чего пропорции тела человека все время меняются. Вурфные же пропорции для любого возраста вычисляются с одним и тем же значением (W(1;1,27;1,40)=1,30; W(1;1,34;1,55)=1,30; W(1;1,39;1,68)=1,30) и оказываются неизменными на протяжении всего времени роста. Постоянная и неизменная величина вурфа свидетельствует о преобразовании форм нашего тела по принципам конформной симметрии. Такая же картина открывается и для других блоков: плеча — предплечья — кисти; фаланг пальцев; туловища, верхней и нижней конечностей тела и т.д.
Значения вурфов немного варьируются, составляя в среднем величину W = 1,31. В идеальном случае В.Петухов указывает W = 1,309, что при выражении через величину золотого сечения равно Ф2/2 (второе вправо число от числа 2 матрицы 5 — A. Ч). Он называет его "золотым вурфом" ...
Вурфные пропорции позволяют, следовательно, выявить конформно-симметричные группы, иными словами, группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные — общность некоторого множества трехчленных соотношений."
Следует отметить, как показал еще А.А. Пилецкий, что древнерусские зодчие были не просто знакомы с существованием вурфов, но и в своей повседневной работе постоянно использовали их. И вот здесь он также обращается к тому самому новгородскому облому, основное предназначение которого Б.А. Рыбаков определил как расчерчивание кружал и дуг. А.А. Пилецкий, опираясь на деления, нанесеные на три грани и равные соответственно а = 5,919 см; b = 7,317 см; с = 8,358 см, находит их пропорциональность Ф и вурфные взаимосвязи. Соотношения самих делений таковы: 2а/b = 1,618 = Ф, 4а/Зb = 0,944 (третье число в строке матрицы 5 влево от числа 0,5 — A.Ч.).
«Суть инструмента состояла в том, чтобы целыми числами его делений строить не только эстетически совершенные виды архитектурных пропорций (невозможные по причине их иррациональности), но и широкий класс трехчастных вурфных пропорций. Если взять по одному делению в возрастающем порядке, то вычисляется вурф W(5,919; 7,318; 8,358), или в буквенном обозначении W(а, b, с) = 1,31; 1,309 = Ф2 /2.
Таким образом, наиболее простое соотношение делений сразу же дает золотой вурф. Если же взять деления в том же порядке, но по количествам За, 2в, 1с, то вурф W(Зa, 2b, 1с) = 1,250, что равно квадрату функции Жолтовского (1,118)2 = 1,250 (или вурфу из системы: W(1; Ф2; Ф4) = 1,25).
Инструментом новгородских зодчих можно построить много групп трехчленных пропорций с различными значениями вурфов, откладывая определенное количество его делений. Например, следующие соотношения делений, помимо упомянутого {а, b, с), дают такое же или близкое значение вурфа 1,309:
W(14a,10b,7с) - 1,309,
W(17а,10b,6с) - 1,308,
W(6a,10b,23с) - 1,310 и т.д.»
Что же дает в архитектуре пропорционирование конструкции в соответствии с золотым вурфом? Ведь в отличие от изменяющегося со временем организма оно всегда остается неизменной.
Однако неизменность конструкции на самом деле кажущаяся. Наблюдатель всегда перемещается относительно конструкции и рассматривает ее под самыми различными углами зрения, а вместе с изменением угла зрения меняется и пропорциональность составных частей конструкции.
И если конструкция имеет вурфное отношение трехчленного деления, то как бы ни перемещался наблюдатель относительно ее, угол зрения А, В и т. д. всегда будет иметь одно и то же значение вурфа. На рис. 9 W=1,333 (рис.9 взят из [15]), и движущийся наблюдатель будет воспринимать постоянно меняющуюся, остающуюся эстетически совершенной, гармоничную конструкцию.
Именно гармоничность архитектурных сооружений как некоторых аналогов природных образований вписывается в пространственные и энергетические взаимодействия природы и обусловливает благотворное влияние Среды на психическое и социальное состояния человеческого общества.
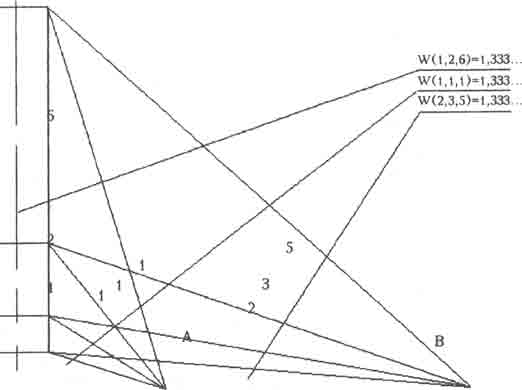
Рис.9. Вурфное пропорционирование
«Если же, как справедливо отмечает А.А. Пилецкий [13], пропорции окружающих нас произведений архитектуры принадлежат к случайным семействам, как в большинстве современных сооружений, то человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна. Такая Среда, не обладающая ни одной из групп характеристических симметрии человека, чаще всего не воспринимается им, а нередко отвергается. Вот где корень неблагоприятного психофизического воздействия Среды на человека, а не только в том, что жилые дома представляют собой набор однотипных "коробок" ».
Мы остановились подробно на разработке и применении вурфов в биологии и архитектуре, во-первых, потому, что они очень наглядны и отображают процесс взаимосвязи явлений во времени и в движении, а во-вторых, потому, что применение системы вурфов находится в стадии становления и не вышло, по-видимому, за пределы научных направлений.
Таблица 5 Серия Пашена
Нахождение золотого вурфа W=1,309 и вурфа W=1,250 на основе золотых пропорций следует отнести к числу выдающихся научных достижений В.Петухова. Но природа не ограничивается только этими вурфами и только золотой пропорцией. Все числовые структуры диагоналей русской матрицы — числа базисных вертикали и горизонтали при любых знаменателях также образуют свои вурфы и по пропорции (9) и по бесчисленному количеству других диагональных пропорций, которые в общей форме могут быть записаны следующим образом: имеем степенной числовой ряд, у которого каждое последующее число от базисного есть результат умножения на постоянный знаменатель, свой для каждой диагонали:
| а, b, с, d,..., k, l, m, ...,s,.... | (10) |
Тогда этот ряд образовывает бессчетную систему вурфов, и каждый из этих вурфов может оказаться аналогом некоторого процесса или структуры:
| W(а,b,...,s) = (а+b+...+d(b+с+...+k)(с+d+...+l) х х (m+n+... +s).../(b+с+... +k)(а+b+с+... +s). | (11) |
Правая часть уравнения (11) может содержать различные комбинации степенных чисел как в числителе, так и в знаменателе. Причем, сами числа также могут возводиться в степени при непременном условии пропорциональной последовательности как возведения, так и порядка их расположения. Например, следующий вурф для Ф находится из уравнения:
W(Ф, Ф3, Ф9) = (1+Ф3)(Ф3+Ф9)/Ф3(1+Ф3+Ф9).
Ряд (11) характеризуется тем, что уже три последовательных числа, взятые в любой части ряда, определяют его степенную пропорциональность, что и обусловливает нахождение характеристических вурфов любой диагонали по этим трем числам. А это достаточно веское основание для выделения числа 3 из всего ряда натуральных чисел.
Значение вурфа и возможность его применения в биологии показана в работе [14], в архитектуре — в работах [10,13,15], однако, это весьма скромное начало. Вурф — понятие общенаучное и обусловливает гармоничное пропорционирование всех процессов и структур природы и не только по золотому сечению. Не случайно об этом упоминает А.А. Пилецкий [15], когда отмечает, что наличие пропорций золотого сечения в основных размерах храма Василия Блаженного просматривается только в сооружении церкви Покрова, а в остальном окружении не замечается, и, тем не менее, весь ансамбль пронизан строгой соразмерностью и пропорциональностью. И это достигается, по-видимому, применением не только золотого вурфа. Приведем пример наличия вурфных отношений в пропорциях спектральных линий водорода. Наиболее известными спектральными линиями водорода являются серии Лаймана, Бальмера, Пашена. Запищем их в таблицу 5.
Таблица 5.
| Серия Лаймана 1215,67 1025,70 972,54 949,74 937,80 930,75 926,23 923,15 920,96 | Серия Бальмера 6562,80 4861,30 4340,65 4101,70 3970,00 3889,10 3835,40 3797,90 | Серия Пашена 18751 12818 10938 10049 9546 9229 9014,9 |
Просчитав величину вурфов по уравнению (9) последовательно снизу вверх по каждому столбцу, найдем, что величина эта для каждого результата своя и в целом для всех линий варьируется от 1,33355 до 1,3764, т.е. в пределах 3%. Варьирование можно объяснить несколькими способами, но наиболее вероятное объяснение, что водородный атом испускает много фотонов, как бы не входящих в эти серии, и их отсутствие изменяет величину вурфа. Кроме того, на «расплывание» вурфа оказывают влияние и особенности испускания фотонов в различных физических процессах.
Теперь, имея вурф водородных линий, определим, какой коэффициент матрицы 5 образует с точностью до четвертого знака аналогичной величины вурф. Этот коэффициент равен 1,0192975..., квадрат 1,038967... (обратная величина числа 1/1,019... = 0,98107.. выделена жирным шрифтом в матрице 6). Определим теоретический вурф W спектральных линий:
W(1;1,01929...;1,0389...) = (1+1,019...)(1,019...+1,0389...)/
/1,019...(1+1,019+1,0389) = 1,33343,
а это означает, что все три серии спектральных линий водорода изменяются пропорционально некоторому коэффициенту k и числу 1,01929... Найдем этот коэффициент, для чего разделим предпоследние числа серий на последние:
к1 = 923,15/920,96 = 1,002378... к2 = 1,009874, k3 = 1,02375...
Получаем:
k14 = k2; k110 = k3; k18 = 1,01918,
и, следовательно, системы спектральных линий водорода в пределах принятой точности измерения кратны k. Для нахождения коэффициента кратности необходимо иметь не менее трех численных параметров рассматриваемой системы.
Вурф позволяет не только проследить принадлежность некоторого параметра тому или иному процессу, характер его изменения, но и определить «полноту» ряда показателей, относящихся к нему. Так, для примера отметим, что во всех теоретических разработках квантовой физики постулируется, что орбиты электрона атома водорода являются стационарными и нумеруются целыми числами n, пробегающими бесконечный ряд значений n = 1, 2, 3 ... , и потому никаких промежуточных орбит в структуре атома отыскать невозможно. Проверим этот постулат по вурфному отношению для радиусов а, скоростей υ, частот v и энергий Е. Выпишем в таблицу 6 значения данных параметров для первых десяти орбит.
Таблица 6
| № орбит | a | υ | v | E |
| 0,5292 | 2,188 | 6,580 | 2,180 | |
| 2,117 | 1,094 | 0,8225 | 0,545 | |
| 4,763 | 0,7293 | 0,2437 | 0,242 | |
| 8,468 | 0,5470 | 0,1028 | 0,136 | |
| 13,23 | 0,4376 | 0,0526 | 0,087 | |
| 19,05 | 0,3647 | 0,0305 | 0,0606 | |
| 25,95 | 0,3126 | 0,0192 | 0,0445 | |
| 33,87 | 0,2735 | 0,0129 | 0,0341 | |
| 42,87 | 0,2431 | 0,0090 | 0,0269 | |
| 52,92 | 0,2188 | 0,0066 | 0,0218 |
Составим для каждого параметра вурфные уравнения по первым трем строкам ( W1), по 6-8 строкам (W2 ) и по 8-10 строкам ( W3 ). Для а имеем:
W1а = 1,1607; W2а = 1,3155; W3а = 1,3225.
Находим для υ:
W1υ = 1,3337; W2υ = 1,3356; WЗυ = 1,3347.
То же для v:
W1v = 1,2550; W2v = 1,3274; W3v = 1,3319.
И, наконец, для энергии Е:
W1Е = 1,3263; W2Е = 1,3336; WЗЕ = 1,3337.
Резкий скачок вурфа с W1а = 1,1607 до W2а = 1,315 с последующим усредненным выравниванием на отметке 1,328 показывает, что на пространстве орбит с номерами от 1 до 6 имеются «прогалы» — места возможных промежуточных орбит. Эта же картина, хотя и не такая резкая, наблюдается и по остальным параметрам. Более плавное изменение вурфов скорости υ, частоты v и энергии Е объясняется тем, что они «привязаны» к радиусу и «повторяют» его поведение с иной степенной последовательностью. Изменение знаменателя последовательности сглаживает возрастание вурфа. Поэтому, взяв ориентировочно вурф 1,3275... за основу, находим, какой знаменатель таблицы 4 имеет близкую величину. Таким знаменателем оказывается большая терция вертикального ряда 1,259921... . Ее вурф W(1;1,259921;1,5874...) = 1,3274... . А это значит, что радиус электронных орбит, лежащих вне боровской, изменяется с шагом 1,259921. И от первой до второй боровской орбиты укладывается пять промежуточных орбит; между 2-й и 3-й, 3-й и 4-й — по две орбиты; между 4-й и 5-й, 5-й и 6-й — по одной, а дальше последовательности орбит совпадают. Таким образом, оказывается, что орбиты электронов в квантовой механике квантуются не только целыми числами. (Интересно, что в шаг 1,2599... попадают и планеты солнечной системы, и спутники планет [16].) Тем не менее, этот вурф не единственен. Он не исключает возможности существования иного шага орбитальных расстояний.
Не только процессы и явления природы описываются в рамках русской матрицы, но и, по-видимому, все научные направления, как, например, физика, изучающая свойства тел, полностью базируются на коэффициентных зависимостях. Оказывается, что все физические свойства тел качественно связаны степенными величинами малой секунды музыкального гармонического ряда 1,05946... [9,17]. И именно качественная взаимосвязь является основой метода размерностей.
Таким образом, русская матрица является математической структурой, отображающей гармонию внутренних взаимосвязей всех свойств тел, материальных процессов или явлений. Система вурфов, в свою очередь, соединяет казалось бы случайные, произвольные числа в пропорции, определяющие принадлежность этих чисел к некоторым процессам и коэффициентам матрицы.
Поэтому знание русской матрицы в принципе позволяет не только отслеживать развитие любого материального процесса или структуры, включая, по-видимому, экономические, социальные (в том числе государственные), экологические, но и возможности отклонения их от параметров матрицы и, вероятно, корректировать течение этих процессов. Не в этом ли заключалась «опасность» знания матрицы? Не это ли та самая большая тайна, которую жрецы Египта унесли с собой?
