Расчет сопротивления наклонных сечений по поперечной силе

Второстепенные балки армируют сварными каркасами и в отдельных случаях отдельными стержнями.

В учебных целях в курсовом проекте балку необходимо заармировать отдельными стержнями. В этом случае наклонные сечения армируют хомутами и отогнутыми стержнями. При этом хомуты назначают по конструктивным требованиям, а отогнутые стержни определяют расчетом.

Диаметр хомутов d_ω в вязанных каркасах изгибаемых элементов должен приниматься не менее 6мм при высоте балки h_sb 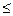800 мм и не менее 8 мм при h_sb > 800 мм. Шаг хомутов S на приопорных участках (1/4 пролета) назначают в зависимости от высоты балки. При высоте балки h_sb ≤ 450 мм не более h_sb/2 и не более 150мм; при h_sb > 450 мм S ≤ h_sb/3 и не более 500 мм. На остальной части пролета при h_sb > 300 мм поперечная арматура устанавливается с шагом S ≤ 3/4·h_sb и не более 500 мм.

В нашем случае принимаем хомуты из стержней класса S500 диаметром 6мм. Шаг хомутов в приопорных участках принимаем 150мм, что меньше h_sb/2 = 400/2 = 200 мм. На средних участках пролетов назначаем шаг хомутов равным 300мм, что меньше ¾: h_sb = 3/4×400=300 мм, а также меньше 500 мм.

Расчет железобетонных изгибаемых элементов на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами должны проверятся по формуле

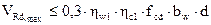(5.6)

где h_w1 – коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента.

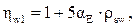но не более 1,3. (5.7)

Отношение модулей упругости арматуры и бетона.

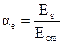, (5.8)

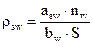, (5.9)

где E_s = 20·10⁴ МПа – модуль упругости для арматуры класса S500;

E_cm = 32·10³ МПа для бетона класса С²⁰/₂₅, марка удобоукладываемости П1, П2;

a_sw = 0,283 см² –для одного стержня диаметром 6 мм;

.

;

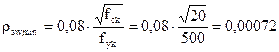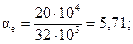
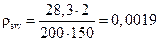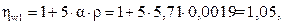
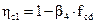; (5.10)

где β₄ – коэффициент, принимаемый для тяжелого бетона равным 0,01.

.

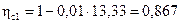Уточняем значение рабочей высоты сечения:d = 400 – 25 = 375 мм.

.

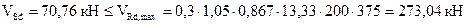Следовательно, прочность по наклонной полосе между наклонными трещинами обеспечена.

Вычисляем поперечную силу, которую могут воспринять совместно бетон и поперечная арматура по наклонной трещине по формуле

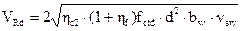, (5.11)

где h_с2 = 2 для тяжелого бетона;

h_f – коэффициент, учитывающий влияние сжатых свесов полки:

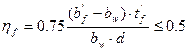(5.12)

где

(b_f’– b_w) ≤ 3 × t_f’;

(b_f’– b_w) = 1750 – 200 = 1550 > 3 × t_f’= 3·60 = 180 мм.

Следовательно, принимаем при расчете (b_f’– b_w) = 180 мм.

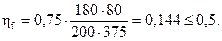
Находим линейное усилие, которое могут воспринять хомуты по формуле

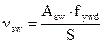, (5.13)

где f_ywd – расчетное сопротивление поперечной арматуры (приняты поперечные стержни Æ6 S500 с A_sw = 28,3 мм², шаг 150 мм); f_ywd=313 МПа.

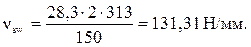
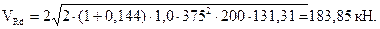
Поперечная сила которую могут воспринять хомуты и бетон V_Rd = 183,85 кН > V_Sd = 70,76 кН, следовательно, прочность наклонного сечения обеспечена.

Построение эпюры материалов

С целью экономичного армирования и обеспечения прочности сечений балки строим эпюру материалов, представляющую собой эпюру изгибающих моментов, которые может воспринять элемент по всей своей длине. 3начение изгибающих моментов в каждом сечении при известной площади рабочей арматуры вычисляют по формуле

M_Rd=f_yd∙A_st∙d∙η, (5.14)

где d – уточненное значение рабочей высоты сечения;

η – табличный коэффициент, определяемый как

η = 1 – 0,5∙ξ, (5.15)

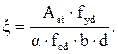(5.16)

При построении эпюры материалов считают, что обрываемый стержень необходимо завести за точку теоретического обрыва, где он уже не нужен по расчету прочности нормальных сечений, на расстояние анкеровки ℓ_bd.

Для построения эпюры материалов по фактической площади арматуры A_st^пр в середине пролета и на опоре определяют момент M_Rd, воспринимаемый арматурой A_st^пр. Затем в масштабе, принятом для построения эпюры изгибающих моментов, проводят горизон­тальную линию, соответствующую A_st^пр.

Эта горизонтальная линяя должна быть расположена несколько дальше эпюры изгибающих моментов по отношению к нулевой линии, что показывает, на сколько фактическая арматура A_st^пр близка к расчетной A_st^тр. Если горизонтальная линия пересекает эпюру изгибающих моментов, то это говорит о том, что арматуры A_st^пр поставлено недостаточно, или сделана в вычислени­ях ошибка.

Затем подсчитывают момент M_Rd для меньшего количества стержней, что будет соответствовать обрыву (отгибу) стержней в сечениях с меньшим изгибающим моментом. Обычно обрывают (отгибают) сразу по два или по од­ному стержню и начинают при этом обрыв (отгиб) с арматуры, расположенной во втором ряду или в средней части при однорядном расположении. При вы­полнении обрывов (отгибов) стержней необходимо соблюдать принцип сим­метрии расположения стержней в поперечном сечении балки.

Зная новое значение M_Rd, снова проводят горизонтальную линию на эпюре изгибающих моментов. Точка пересечения этой линии с эпюрой момен­тов и будет точкой теоретического обрыва (отгиба). Таким же образом посту­пают и при определении мест обрыва (отгиба) других стержней.

Из точек теоретического обрыва (т.т.о.) проводят перпендикулярные ли­нии до пересечения их с горизонтальными линиями M_Rd и окончательно стро­ят эпюру материалов, которая имеет ступенчатый вид в местах теоретическо­го обрыва стержней, и наклонный вид в местах отгиба стержней. Следует иметь в виду, что начало каждого отгиба в растянутой зоне располагают на расстоянии точки теоретического обрыва не менее чем 0,5∙d, где d – уточненное значение рабочей высоты сечения.

При выполнении обрывов (отгибов) стержней необходимо соблюдать принцип симметрии расположения стержней в поперечном сечении балки. С целью восприятия изгибающего момента от возможного частичного защемления балки на стене в первом пролете арматуру не обрывают, а отгибают на крайнюю опору. Начало отгиба располагают на расстоянии 50–60 мм от внутренней грани стены.

Из точек теоретического обрыва обрываемых стержней по горизонтали откладывают длину анкеровки ℓ_bd и окончательно устанавливают место фак­тического обрыва стержня.

Расчеты, необходимые для построения эпюры материалов выполнены в табличной форме.

Таблица 3.4 – Вычисление ординат эпюры материалов для продольной арматуры

Диаметр и количество стержней	Уточненная высота сечения d = hsb – c, мм	Фактическая площадь сечения стержней, Ast, мм2	Расчетное сопротивление арматуры fyd, МПа	Относительная высота сжатой зоны,	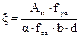Коэффициент η = 1 – 0,5∙ξ	Момент MRd = fyd∙Ast∙d∙η, кН∙м
Первый пролет (нижняя арматура b = 1750 мм, с = 25 мм)
2Ø14				0,015	0,993	50,41
1Ø10				0,004	0,998	13,02
Первый пролет (верхняя арматура b = 200 мм, с = 25 мм)
2Ø10				0,0696	0,965	25,19
Опорная арматура. Опора В (верхняя арматура b = 200 мм, с = 50 мм)
2Ø12				0,107	0,946	33,14
1Ø12				0,052	0,974	16,32
Опорная арматура. Опора В (нижняя арматура b = 200 мм, с = 50 мм)
2Ø10				0,075	0,963	23,45
Второй пролет (нижняя арматура b = 1750 мм, с = 25 мм )
2Ø10				0,008	0,996
1Ø12				0.0055	0,997	17,89
Второй пролет (верхняя арматура b = 200 мм, с = 25 мм)
2Ø10				0,0696	0,965	25,19
Опорная арматура. Опора С (верхняя арматура b = 200 мм, с = 50 мм)
2Ø12				0,107	0,946	33,14
1Ø10				0,037	0,981	11,95
Опорная арматура. Опора С (нижняя арматура b = 200 мм, с = 50 мм)
2Ø10				0.075	0.963	23,45

Сопоставляя эпюру материалов с огибающей эпюрой моментов, можно определить запас прочности (расстояние между эпюрой моментов и эпюрой материалов) в любом сечении по всей длине балки. Эти эпюры не должны пересекаться. Чем ближе эти эпюры подходят к огибающей эпюре моментов, тем экономичнее и рациональнее заармирована балка.

Теоретическое место обрыва стержней определяем графическим путем.

Эпюра материалов представлена на рисунке 5.4.

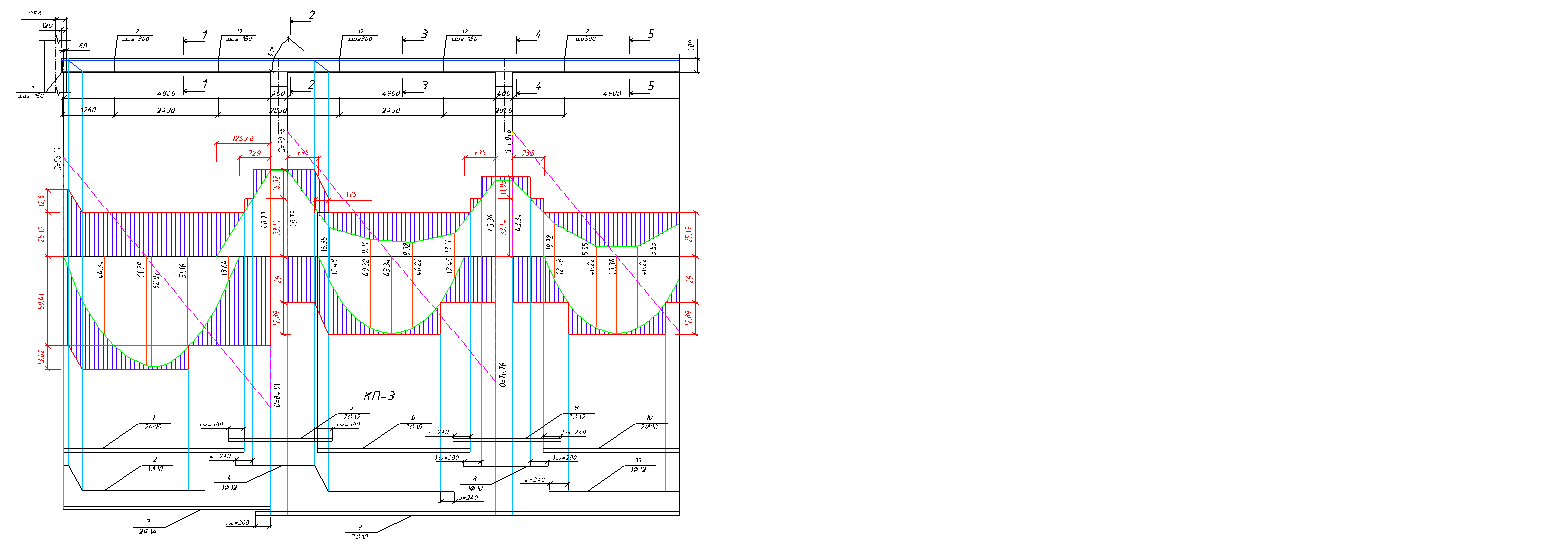Рисунок 5.4 – Эпюра материалов для второстепенной балки