Кафедра гидравлики, водоснабжения и водоотведения

Кафедра гидравлики, водоснабжения и водоотведения

ПРОГНОЗИРОВАНИЕ ТЕХНИЧЕСКОГО СОСТОЯНИЯ СИСТЕМ ВОДОСНАБЖЕНИЯ И ВОДООТВЕДЕНИЯ

Методические указания и контрольные задания для студентов специальности 270112.65 – «Водоснабжение и водоотведение»

Иваново 2010

УДК 628.1

Прогнозирование технического состояния систем водоснабжения и водоотведения: Методические указания и контрольные задания для студентов специальности 270112.65 – «Водоснабжение и водоотведение» / Иван. Гос. архит.-строит. ун-т; Сост.: М.Ю. Ометова, Б.В. Жуков. – Иваново, 2010 – 32 с.

Методические указания содержат краткий теоретический материал, необходимый для выполнения контрольной работы, варианты контрольных заданий, справочный материал.

Методические указания предназначены для выполнения контрольной работы по дисциплине «Обследование, диагностика, реконструкция систем водоснабжения и водоотведения» для студентов специальности 270112.65 – «Водоснабжение и водоотведение».

Рецензент–доктор технических наук, профессор кафедры гидравлики, водоснабжения и водоотведения ИГАСУ Н.Н. Елин.

Составители

Ометова Мария Юрьевна

Жуков Борис Вячеславович

ПРОГНОЗИРОВАНИЕ ТЕХНИЧЕСКОГО СОСТОЯНИЯ СИСТЕМ ВОДОСНАБЖЕНИЯ И ВОДООТВЕДЕНИЯ

Методические указания и контрольные задания для студентов специальности 270112.65 – «Водоснабжение и водоотведение»

Печатается в авторской редакции

Содержание

	Прогнозирование изменения технического состояния объектов диагностирования………………………………..
1.1.	Задачи прогнозирования ……………………………….
1.2.	Основные термины и понятия теории надёжности………..
	Задания на контрольную работу…………………………...
2.1.	Определение количественных характеристик надежности по статистическим данным об отказах изделия ……..
2.2	Аналитическое определение количественных характеристик надежности…………………………………………….
2.3.	Последовательное соединение элементов в систему…….
2.4.	Расчет надежности резервированной системы с параллельным включением элементов……………………
2.5.	Комплексные показатели надежности……………………
	Приложение………………………………………………
	Библиографический список……………………………….

Задачи прогнозирования

Термин прогноз происходит от греческого слова prognosis, что означает предвидение, предсказание о развитии чего-либо, основанное на определённых данных. Точность прогноза зависит от того, какой закон используется и насколько правильно и точно он осознан.

Прогнозирование – составление прогноза развития, становления, распространения чего-либо, например, науки, надёжности на основании тщательно отобранных данных. Прогнозирование возможно, если в случайном процессе, характеризующем изменение параметра, можно выделить тренд (trend – тенденция), т.е. сделать предположение о существовании закономерностей, определяющих износ и старение.

При решении задач прогнозирования находят применение два понятия:

Интерполяция (лат. interpolation – изменение), означает определение промежуточных значений функции по известным её значениям.

Экстраполяция (лат. extra + polire – сверх + гладкий), характеризует определение значений функции за пределами интервала, где известны её значения.

В диагностике прогнозируют изменение технического состояния объекта диагностирования (ОД) на основе данных об изменениях, происходящих в объекте с течением времени под влиянием внешних воздействий и внутренних физико-химических превращений.

Прогнозирование вполне осуществимо при наличии постепенных отказов. К постепенным отказам можно отнести снижение давления в напорных трубопроводах, загрязнение фильтров, увеличе6ние потребления энергии двигателями и др. Прогнозировать постепенные отказы – значит определять через какой промежуток времени контролируемый параметр выйдет за допустимые пределы. Прогнозировать внезапные отказа сложнее, но при наличии статистического материала о закономерностях их возникновения можно ориентировочно определить время наступления отказа и принять меры для его устранения.

Различают три вида математического прогнозирования:

1. аналитическое, основанное на степенных рядах и уравнениях регрессии;

2. вероятностное, основанное на теории вероятности;

3. статистическая классификация, основанная на теории распознавания образов.

Так как в настоящее время объекты и системы ВиВ не имеют накопленных в достаточном количестве данных об отказах и времени их восстановления. В условиях ограниченной информации рекомендуется использовать статистический метод прогнозирования надёжности, который наиболее полно описывает эксплуатационное состояние [2].

Решение задачи прогнозирования для конкретного объекта позволит:

· выявить элементы объекта, работоспособность которых изменится в ближайший интервал времени;

· определить сроки проведения профилактических и ремонтных работ;

· обоснованно решать вопросы замены запасных частей на весь период использования объекта.

Прогнозировать состояние систем ВиВ можно не только по статистическим данным, но и по КИП (контрольно-измерительным приборам) и на основании показаний приборов делать выводы о техническом состоянии объекта.

1.2. Основные термины и понятия теории надёжности

Надёжность как наука, возникла в середине прошлого века из потребности разобраться в отказах радиотехнического оборудования, элементы которого характеризует статическая устойчивость однородных событий. Ниже приведены основные термины и понятия теории надёжности [1], [2]:

Надёжность – комплексное свойство, состоящее в общем случае из безотказности, долговечности, ремонтопригодности и сохраняемости. Например, для неремонтируемых объектов основным свойством может являться безотказность. Для ремонтируемых объектов одним из важнейших свойств, составляющих понятие надежности, может быть ремонтопригодность.

Безотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки.

Долговечность – свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Для невосстанавливаемых объектов понятие безотказности и долговечности совпадают.

Безотказность и долговечность являются основными параметрами надежности, в определенной мере управляемыми при эксплуатации инженерных систем.

Например, применительно к трубопроводам подземной прокладки эти два понятия можно трактовать следующим образом [3]:

– безотказность – свойство трубопроводов непрерывно обеспечивать пропуск воды с расчетными параметрами (давление, расход, качество и т. д.) и сохранять герметичность в течение заданного промежутка времени;

– долговечность – свойство трубопроводов выполнять свои функции с возможными отключениями для осуществления ремонтов до наступления предельного состояния.

Ремонтопригодность – свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта.

Сохраняемость – свойство объекта сохранять в заданных пределах значения параметров, характеризующих способности объекта выполнять требуемые функции в течение и после хранения, или транспортирования.

Надежность объектов оценивается временными понятиями, такими как наработка, наработка до отказа, наработка между отказами, время восстановления, и т.д.

Наработка – продолжительность или объем работы объекта. Наработка может быть как непрерывной величиной (продолжительность работы в часах, километраж пробега и т. п.), так и целочисленной величиной (число рабочих циклов, запусков и т. п.)

Наработка до отказа – наработка объекта от начала эксплуатации до возникновения первого отказа.

Наработка между отказами – наработка объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа.

Время восстановления – продолжительность восстановления работоспособного состояния.

Отказ – событие, заключающееся в нарушении работоспособности объекта.

ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ

Контрольная работа по дисциплине: «Обследование, диагностика реконструкция систем ВВ» состоит из 10 прикладных задач по следующим темам: обработка статистики отказов, определение показателей надёжности оборудования систем ВиВ, показатели ремонтопригодности и комплексные показатели надёжности. Задачи содержат методические указания необходимые для их решения. Исходные данные к задачам 3 – 10 приведены непосредственно в тексте задачи. Номер варианта соответствует последней цифре номера зачётной книжки.

Физический смысл.

Величина Р(t_i) характеризует долю работоспособных изделий к моменту времени t_i.

Рис. 1. Кривая распределения вероятности

безотказной работы

Вероятность безотказной работы по статистическим данным об отказах оценивается выражением

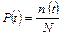(1)

где n(t) – число изделий, неотказавших к моменту времени t; N – число изделий, поставленных на испытания; Р(t) – статистическая оценка вероятности безотказной работы изделия. Типичный график функции Р(t) представлен на рис. 1 и называется в специальной литературе «кривой убыли».

Для вероятности отказа по статистическим данным справедливо соотношение 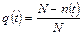(2)

(2)

где N–n(t) – число изделий, отказавших к моменту времени t; Р (t) – статистическая оценка вероятности отказа изделия.

Частота отказов по статистическим данным об отказах определяется выражением

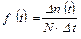(3)

где Δn(t) – число отказавших изделий на участке времени (t, t+Δt); f(t) – статистическая оценка частоты отказов изделия; Δt – интервал времени.

Большинство современных исследований надежности систем водоснабжения и водоотведения в качестве показателей безотказности используют вероятность безотказной работы или производный от него показатель – интенсивность отказов λ(t):

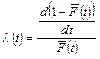
Физический смысл интенсивности отказов – это мера, выражающая склонность объекта к отказу в зависимости от времени его эксплуатации.

Интенсивность отказов (условная плотность вероятности отказов) по статистическим данным об отказах определяется формулой:

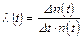(4)

где n(t) – число изделий, не отказавших к моменту времени t; Δn(t) – число отказавших изделий на участке времени (t, t+Δt); λ (t) – статистическая оценка интенсивности отказов изделия.

Для решения задач о прогнозировании работоспособности необходима математическая модель, которая должна быть представлена аналитическим выражением интенсивности отказов λ(t). Типичная кривая распределения отказов представлена на рис. 2. Вероятность безотказной работы и интенсивность отказов являются функциями времени формулы (1), (4). Причем, вероятность безотказной работы – всегда убывающая функция, (рис. 1), а интенсивность отказов может быть как возрастающей функцией, так и неизменной (рис. 2).

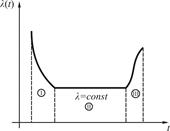Кривую изменения отказов можно условно разделить на три характерных участка:

первый (I) – период приработки,

второй (II) – период нормальной эксплуатации,

третий (III) – период старения объекта.

Рис. 2. Кривая изменения интенсивности отказов

во времени

Отказы, появляющиеся в периоде нормальной эксплуатации, называют внезапными, так как они появляются в случайные моменты времени, т.е. внезапно, непредсказуемо.

Интенсивность отказов постоянна тогда и только тогда, когда функция распределения наработки F(t) = 1– F (t) распределена по экспоненциальному закону.

Средняя наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Среднее время безотказной работы оборудования (средняя наработка до первого отказа) по статистическим данным оценивается выражением

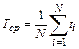(5)

где t_i – время безотказной работы i-го изделия; N – общее число изделий, поставленных на испытания; Т_ср – статистическая оценка среднего времени безотказной работы изделия.

Для определения Т_ср по формуле (5) необходимо знать моменты выхода из строя всех N изделий. Можно определять Т_ср из уравнения

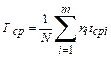(6)

где n_i – количество вышедших из строя изделий в i-ом интервале времени; t_ср.i = (t_i-1+t_i)/2; m=t_k/Δt; Δt=t_i+1–t_i; t_i–1 – время начала i-го интервала; t_i – время конца i-го интервала; t_k – время, в течение которого вышли из строя все изделия; Δt – интервал времени.

Дисперсия времени безотказной работы изделия по статистическим данным определяется формулой

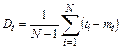(7)

где D_t – статистическая оценка дисперсии времени безотказной работы изделия.

Задача 1.

На испытании находилось N₀ = 100 образцов неремонтируемого оборудования. Число отказов оборудования n (Dt) фиксировалось через каждые 200 часов работы. Данные об отказах оборудования приведены в табл. 1. По этим опытным данным вычислить количественные показатели надежности:

1. Р(t) – вероятность безотказной работы за время t;

2. f (t) – частота отказов за время t;

3. l (t) – интенсивность отказов за время t;

4. T_ср – средняя наработка до первого отказа, час.

Построить графики зависимостей этих характеристик от времени

Таблица 1

Dt, час	0-	200-	400-	600-	800-	1000-	1200-1400
n (Dti)

Продолжение табл.1

Dt, час	1400-	1600-	1800-	2000-	2200-	2400-
n (Dti)

Продолжение табл. 1

Dti ,час	2600-	2800-
n (Dti))

Задача 2.

Построить график распределения случайной величины, числа снижений (ниже допустимого) объёма подачи воды некоторому потребителю, т.е. число отказов. Наблюдения велись в течение 20 лет. Результаты наблюдений представлены в табл. 2.

Таблица 2

Годы наблюдений
Число отказов в год

Продолжение табл. 2

Годы наблюдений
Число отказов в год

Задача 3.

В течение некоторого времени проводилось наблюдение за работой N₀ экземпляров восстанавливаемых изделий. Каждый из образцов проработал t_i часов и имел n_i отказов. Требуется определить среднюю наработку на отказ по данным наблюдения за работой всех изделий. Исходные данные для расчета приведены в табл. 3.

Таблица 3

вари- ант	Исходные данные
n1	t1, ч.	n2	t2,ч.	n3	t3, ч.	n4	t4, ч.	n5	t5, ч.
							–	–	–	–
									–	–
							–	–	–	–
									–	–
									–	–
									–	–
							–	–	–	–

Задача. 4.

Определить суммарное значение интенсивности отказов λ_с и вероятности безотказной работы через 100, 1000, 2000, 4000, 8000 ч непрерывной работы. Принципиальная схема рассматриваемой системы приведена на рис.3. Снижение вероятности безотказной работы менее 0,7 считать отказом системы. Если предпоследняя цифра зачётной книжки от 0 – 4, то студент принимает стальные трубы, если от 5 – 9 – чугунные.

Значение интенсивности отказов отдельных элементов санитарно-технических систем приведены в приложении (табл. П1). Исходные данные к задаче приведены в табл. 4.

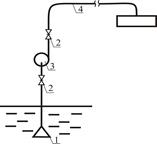1 – приёмный клапан;

2 – задвижка;

3 – насос;

4 – трубопровод.

Рис. 3.Расчётная схема

Таблица 4

Вариант	L, см	Диаметр трубопровода, мм	Марка насоса
			ЭЦВ 4
			ЭЦВ 6
			ЭЦВ 8
			ЭЦВ 10
			ЭЦВ 6
			ЭЦВ 10
			ЭЦВ 4
			ЭЦВ 8
			ЭЦВ 6
			ЭЦВ 8

Методические указания к решению задачи 4.

При анализе статистических данных об отказах отдельных элементов, составляющих систему, установлено, что значение интенсивности отказов λ колеблется в пределах от λ_max до λ_min. В этом случае вероятность безотказной работы будет иметь вид, представленный на рис. 4.

Расчёт надёжности целесообразно производить в следующей последовательности: рассматривается принципиальная схема, устанавливается связь между отдельными элементами системы, сложные системы разбиваются на подсистемы, которые в свою очередь на группы, узлы, составляется структурная схема, составляется таблица расчёта надёжности, по данным таблицы рассчитываются количественные показатели надёжности блоков, подсистем, и системы в целом.

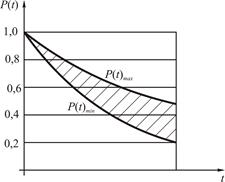
Рис.4.Зависимость р(t) от времени

В принципиальных (функциональных) схемах показываются реальные связи между элементами системы: электрические, кинематические и др. Каждый элемент этой системы показывает конкретную технологическую принадлежность.

В структурных схемах показывают лишь те связи, которые отражают надёжность системы, при выполнении заданных функций.

Задача 5.

(если последняя цифра зачётной книжки от 0 до 4) время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром λ. Определить количественные характеристики надёжности: вероятность безотказной работы, вероятность отказа, частоту отказов и среднее время безотказной работы для времени t. Исходные данные для задачи принять по табл. 5.1.

(если последняя цифра зачётной книжки от 5 до 9) время работы элемента до отказа подчинено закону распределения Релея. Требуется вычислить количественные характеристики надёжности элемента: вероятность безотказной работы, частоту отказа, интенсивность отказа, среднее время безотказной работы для времени t, если параметр распределения σ. Исходные данные для задачи принять по табл. 5.2.

Таблица 5.1

	Варианты
λ·104, 1/ч							1,5	0,8	1,9
t, ч

Таблица 5.2

	Варианты
σ, ч
t, ч

Задача 6.

Изделие состоит из N групп узлов. Отказы узлов первой группы подчинены экспоненциальному закону с интенсивностью отказов l, отказы узлов второй группы – закону Релея с параметром s, отказы узлов третьей группы – экспоненциальному закону с интенсивностью отказов l. Требуется определить вероятность безотказной работы изделия в течение времени t. Исходные данные для расчета приведены в табл. 6.

Таблица 6

Варианты	Исходные данные
N	l·10-4, 1/час	s, час	l· 10-4, 1/час	t, час
				0,93
		–		1,8
		3,2	–	2,6
		0,93		–
		0,6		3,2
		0,6		2,8
		0,93	–	1,8
		–		0,93
				0,6
		3,2		0,93

Задача. 7.

Система состоит из N различных невосстанавливаемых блоков, при этом она имеет основное соединение блоков, т.е. отказ любого из блоков приводит к отказу системы. Для блоков справедлив экспоненциальный закон надежности. Средняя наработка до первого отказа для разных блоков различна и равна Т_i часов.

Требуется найти вероятность безотказной работы системы в течение t часов. Найти также интенсивность отказов для системы и среднюю наработку до первого отказа системы. Исходные данные приведены в табл. 7.

Таблица 7

вариант	N	Т1	Т2	Т3	Т4	Т5	Т6	Т7	Т8	t
							-	-	-
									-
								-	-
					-	-	-	-	-
						-	-	-	-
							-	-	-
					-	-	-	-	-
						-	-	-	-
								-	-

Задача 8.

Насосная станция состоит из n однотипных насосов, включенных параллельно, из которых m являются рабочими. Интенсивность отказов каждого из насосов l = 0,2 ^. 10 ^-3 1/час.

Необходимо определить вероятность безотказной работы насосной станции в течение t = 2000 час, а также среднюю наработку до первого отказа. Сделать то же самое для случая, когда резервирования насосов нет, сравнить полученные результаты и сделать вывод об эффективности резервирования.

При решении задачи использовать приведенные выше формулы и табл. 8. Исходные данные приведены в табл. 9.

Таблица 9

вариант	Последняя цифра шифра студента
n
m

Задача. 9.

Один насос из группы питательных насосов имеет среднюю наработку на отказ Т_ср и среднее время восстановления Т_в.

Определить коэффициент готовности насоса, а также интенсивность отказов l и интенсивность восстановления m при экспоненциальном законе надежности. Найти вероятность исправного состояния насоса в течение времени t. Исходные данные представлены в табл. 10.

Таблица 10

	Последняя цифра шифра студента
Тср, час
Тв,час
t , час

Задача. 10.

Система состоит из k групп элементов. В процессе эксплуатации зафиксировано n отказов. Количество отказов в j –й группе равно n_j; среднее время восстановления элементов j–й группы равно t_j. Требуется вычислить среднее время восстановления системы. Исходные данные для расчета приведены в табл. 11. Определить коэффициент готовности изделия после отказа и восстановления, если изделие имело среднюю наработку на отказ 70 часов.

Таблица 11

Вари- ант

Исходные данные

k

n

n1

t1, мин

n2

t2, мин

n3

t3 мин

n4

t4, мин

n5

t5, мин

–

–

–

–

–

–

–

–

–

–

Приложения

Таблица П1

Показатели надёжности водопроводно-канализационного оборудования по данным эксплуатации

Тип оборудования	Интенсивность отказов, λ·104, 1/(ч·км)	Интенсивность ремонтов μ, ч-1
λmin	λmax
Трубы стальные
ø100	0,18	0,4	2–4
ø150	0,16	0,35	2–4
ø200	0,15	0,3	2–4
ø250	0,13	0,25	2–4
ø300	0,12	0,2	2–4
ø400	0,11	0,18	2–4
ø500	0,1	0,15	2–4
ø600	0,1	0,14	2–4
Трубы чугунные
ø100	0,9	1,14	2–4
ø150	0,75	1,09	2–4
ø200	0,7	1,05	2–4
ø250	0,6		2–4
ø300	0,55	0,85	2–4
ø400	0,5	0,74	2–4
ø500	0,47	0,57	2–4
ø600	0,44	0,53	2–4
Сетевые задвижки	0,1	0,8	1–4
Клапаны	0,04	0,08
Насосы
ЭЦВ 4		1,6
ЭЦВ 6	0,8	5,6
ЭЦВ 8	0,8	4,6
ЭЦВ 10	0,9	3,2

Библиографический список

1. ГОСТ 27.002.-89. Надёжность в технике. Основные понятия. Термины и определения.
2. Абрамов, Н.Н. Надёжность систем водоснабжения и водоотведения – М.: Стройиздат, 1984. – 216 с.
3. Калинин, В. М. Оценка безотказности и прогнозирование долговечности трубопроводов подземной прокладки // Сантехника – 2006, №4.
4. Исаев, В.Н., Калинин, В. М. Оценка эксплуатационных качеств систем водоснабжения. // Сантехника – 2006, №2.

Кафедра гидравлики, водоснабжения и водоотведения