Примеры решения задач по теме №1
«Механика и элементы специальной теории относительности»
Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct3, где А = 4 м, В = 2 м/c, С = 0,2 м/с3. Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
Дано:
| x = A + Bt + Ct3 A = 4 м B = 2 м/c C = 0,2 м/c3 t1 = 2 c; t2 = 5 c | Решение 1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1 и t2: x1 = (4+2×2+0,2×23) м = 9,6 м, x2 = (4+2×5+0,2×53) м = 39 м. |
| x1, x2, <u>- ? u1, u2 - ? <a>, a1, a2 - ? | 2. Средняя скорость 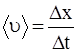 , , |
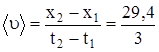 м/с = 9,8 м/с.
м/с = 9,8 м/с.
3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения: 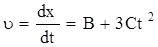
u1 = (2+3×0,2×22) м/с = 4,4 м/c;
u2 = (2+3×0,2×52) м/с = 17 м/с.
4. Среднее ускорение 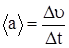 ,
,
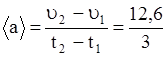 м/c2 = 4,2 м/с2.
м/c2 = 4,2 м/с2.
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1 = 6×0,2×2 м/c2 = 2,4 м/с2;
a2 = 6×0,2×5 м/с2 = 6 м/с2.
Ответ: x1 = 9,6 м; x2 = 39 м; áuñ = 9,8 м/с; u1 = 4,4 м/c; u2 = 17 м/с; áаñ = 4,2 м/с2; a1 = 2,4 м/с2; a2 = 6 м/с2.
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 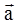 любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.
любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.
Дано:
| w0 = 0 N = 2 e = const | Решение Разложив вектор 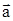 точки М на тангенциальное точки М на тангенциальное 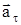 и нормальное и нормальное 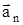 ускорения, видим, что искомый угол определяется соотношением tga=at/an. ускорения, видим, что искомый угол определяется соотношением tga=at/an. |
| a - ? |
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: at = eR, an = w2R, где R – радиус маховика, получим
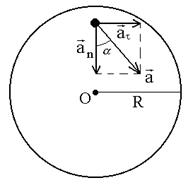 tga =
tga = 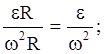
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
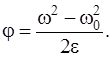
Поскольку w0 = 0; j = 2pN, то w2 = 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:
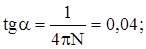 a » 2,3°.
a » 2,3°.
Ответ: a » 2,3°.
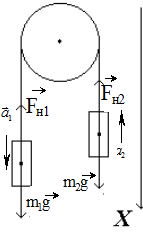
Задача 3 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 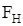 . Трением в блоке пренебречь.
. Трением в блоке пренебречь.
Дано:
| m1 = 2 кг m2 = 1 кг | Решение Воспользуемся для решения задачи основным законом динамики 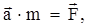 где где 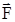 – равнодействующая всех сил, действующих на тело. – равнодействующая всех сил, действующих на тело. |
| a, FН - ? |
На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем
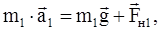 (1)
(1)
 |
для второго тела
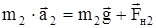 . (2)
. (2)
Так как сила трения в блоке отсутствует,
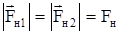 .
.
Ускорения тел а1 и а2 направлены в противоположные стороны и равны по модулю:
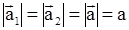 .
.
Получаем из выражений (1) и (2) систему уравнений
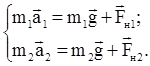
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений
в проекции на ось Х 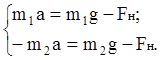
Решая эту систему относительно а и FН, получаем:
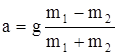 = 3,3 м/с2;
= 3,3 м/с2; 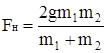 = 13 Н.
= 13 Н.
Ответ: a= 3,3 м/c2 ; FH = 13 Н.
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с2.
Дано:
| R = 0,2 м F = 98,1 Н MТР = 4,9 Н×м e = 100 рад / c2 | Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости: 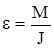 , где , где 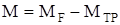 - момент сил, приложенных к телу, - момент сил, приложенных к телу, |
| m - ? |
относительно выбранной оси ( MF - момент силы F, Mтр – момент сил трения);
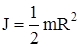 - момент инерции диска.
- момент инерции диска.
Учитывая, что MF=F×R, получаем 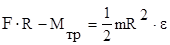 .
.
Отсюда 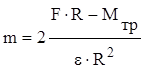 ; m = 7,4 кг.
; m = 7,4 кг.
Ответ: m = 7,4 кг.
Задача 5 На гладкой горизонтальной поверхности находятся две одинаковые соприкасающиеся шайбы. Третья такая же шайба налетает на них со скоростью v0 = 6 м/с, направленной по общей касательной к неподвижным шайбам. После столкновения налетевшая шайба движется вдоль первоначального направления со скоростью v1 = 2 м/с. Найти величину энергии, перешедшей во внутреннюю энергию тел при столкновении. Масса каждой шайбы m = 100 г.

 Решение
Решение
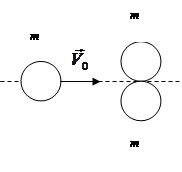 Рассмотрим систему, состоящую из трех шайб. Данная система не является консервативной, так как в условии задачи требуется найти энергию, перешедшую во внутреннюю энергию тел при их взаимодействии. Значит, удар не является абсолютно упругим, и механическая энергия системы не сохраняется. Строго говоря, эта система не является и замкнутой, так как на тела действуют внешние силы тяжести и реакции поверхности, на которой находятся шайбы. Однако эти внешние силы направлены вертикально и их проекции на любую горизонтально проведенную ось равны нулю. Поэтому при описании удара тел можно пользоваться законом сохранения импульса (для его проекций на любую горизонтальную ось).
Рассмотрим систему, состоящую из трех шайб. Данная система не является консервативной, так как в условии задачи требуется найти энергию, перешедшую во внутреннюю энергию тел при их взаимодействии. Значит, удар не является абсолютно упругим, и механическая энергия системы не сохраняется. Строго говоря, эта система не является и замкнутой, так как на тела действуют внешние силы тяжести и реакции поверхности, на которой находятся шайбы. Однако эти внешние силы направлены вертикально и их проекции на любую горизонтально проведенную ось равны нулю. Поэтому при описании удара тел можно пользоваться законом сохранения импульса (для его проекций на любую горизонтальную ось).
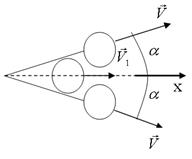 Рассмотрим два состояния выбранной системы тел: 1) налетающая шайба движется со скоростью v0 вдоль горизонтальной оси X, остальные две шайбы покоятся; 2) после частично неупругого удара налетающая шайба движется вдоль оси X с меньшей скоростью v1, а две первоначально покоившиеся шайбы разлетаются со скоростями v2 и v3.
Рассмотрим два состояния выбранной системы тел: 1) налетающая шайба движется со скоростью v0 вдоль горизонтальной оси X, остальные две шайбы покоятся; 2) после частично неупругого удара налетающая шайба движется вдоль оси X с меньшей скоростью v1, а две первоначально покоившиеся шайбы разлетаются со скоростями v2 и v3.
Поскольку размеры всех шайб одинаковы, то скорости v2 и v3, направленные вдоль прямых,
соединяющих центры шайб в момент удара, составляют одинаковые углы a = 30о с осью X, а так как массы всех шайб по условию равны, то очевидно, что скорости v2 и v3 равны по модулю, то есть v2 = v3 = v.
Теперь запишем закон сохранения импульса для проекций импульсов взаимодействующих тел на ось X:
mv0x = mv1x + mv2x + mv3x
Учтем, что v0x = v0; v1x = v1; v2x = v3x = v сosa.
Тогда mv0 = mv1 + 2 mv сosa.
Отсюда 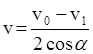 .
.
Энергию, перешедшую во внутреннюю энергию тел при частично неупругом ударе, можно найти как разность кинетической энергии налетающей шайбы до удара и суммарной кинетической энергии всех тел после удара:
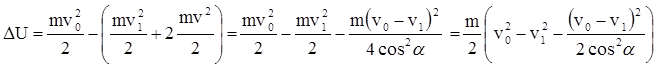 .
.
Сделаем вычисления:
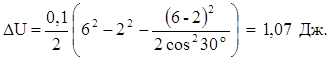
Ответ: DU = 1,07 Дж.
Задача 6 Небольшое тело массой m равномерно втащили на горку, действуя силой, которая в каждой точке направлена по касательной к траектории. Найти работу этой силы, если высота горки h, длина ее основания l, и коэффициент трения m.
 Решение
Решение
Работу, совершаемую силой 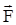 , можно найти по общему определению работы:
, можно найти по общему определению работы:
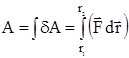 .
.
Для этого необходимо предварительно найти силу 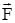 . Рассмотрим перемещаемое тело в произвольной точке траектории его движения. На тело действуют четыре силы: сила тяжести
. Рассмотрим перемещаемое тело в произвольной точке траектории его движения. На тело действуют четыре силы: сила тяжести 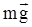 , сила реакции опоры
, сила реакции опоры 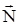 , сила трения скольжения
, сила трения скольжения 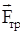 и внешняя сила
и внешняя сила 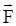 . Поскольку по условию задачи тело движется равномерно, то векторная сумма этих сил равна нулю:
. Поскольку по условию задачи тело движется равномерно, то векторная сумма этих сил равна нулю:
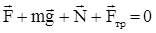
Выберем координатные оси х и у таким образом, чтобы ось х была направлена по касательной к траектории (вдоль перемещения 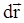 ).
).
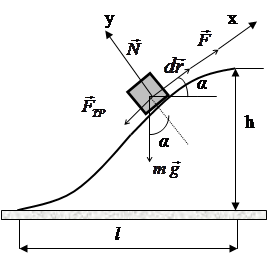
Запишем векторное равенство в проекциях на эти координатные оси:
oсь x: 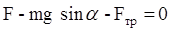
oсь y: 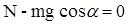
Тогда 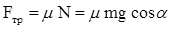 , а модуль силы
, а модуль силы
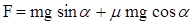 .
.
Теперь можно найти выражение для элементарной работы, совершаемой силой F при перемещении тела на расстояние dr. При этом учтем, что угол между векторами 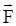 и
и 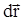 равен нулю и косинус этого угла равен единице.
равен нулю и косинус этого угла равен единице.
Тогда 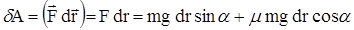 .
.
Из рис. видно, что 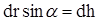 , где dh - элементарное приращение высоты при перемещении тела на расстояние dr, а
, где dh - элементарное приращение высоты при перемещении тела на расстояние dr, а 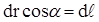 , то есть элементарному перемещению тела в горизонтальном направлении.
, то есть элементарному перемещению тела в горизонтальном направлении.
Тогда 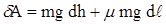 ,
,
и полная работа, совершаемая силой F при втаскивании тела на горку:

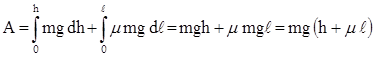 .
.
Ответ: 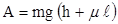 .
.
Задача 7 Круглая платформа радиусом R=1,0 м, момент инерции которой J=130 кг×м2, вращается по инерции вокруг вертикальной оси, делая n1=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.
Дано:
| R = 1м J = 130 кг × м2 n1 = 1c-1 m = 70 кг | Решение Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа + человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме относительно оси, совпадающей с осью вращения и направленной по угловой скорости: |
| n2 - ? |
L1 = L2 , (1)
где L1 - импульс системы «платформа + человек на краю платформы», L2 - импульс системы «платформа + человек в центре платформы».
L1 = J1w1 = (J+mR2)×2pn1, (2)
L2 = J2w2 = J×2pn2, (3)
где mR2 - момент инерции человека, J1 = J+mR2 - момент инерции системы «платформа + человек на краю платформы», J2 - момент инерции системы «платформа + человек в центре платформы», w1 и w2 - соответствующие угловые скорости системы. Решая систему уравнений (1) - (3), получаем
n2 = n1(J+mR2)/J = 1,5 об/с.
Ответ: n2 = 1,5 с-1.
Задача 8 В условно неподвижной системе отсчета К в точках с координатами xA и xB = xA + l, где l = 1 км, одновременно происходят два события A и B. На каком расстоянии l¢АВ друг от друга зафиксирует эти события наблюдатель в системе К¢, движущейся со скоростью v = 0,4×с вдоль оси X? Какой промежуток времени Dt¢ между этими событиями зафиксирует наблюдатель в системе К¢?
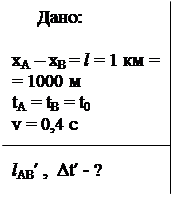 Решение
Решение
Обозначим через t0 момент времени, когда в системе К происходят события А и В. Тогда событие А в этой системе обладает пространственно – временными координатами xA и t0, а событие В – координатами xB и t0. В системе К¢ событие А обладает пространственно–временными координатами x1¢ и t1¢, а событие В – координатами x2¢ и t2¢. Связь координат каждого из событий можно записать с помощью преобразований Лоренца.
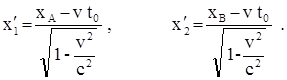
Найдя разность этих выражений, получим расстояние между точками, в которых происходят события А и В в системе К¢.
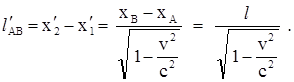
Видно, что расстояние l¢АВ, разделяющее события А и В в любой системе, движущейся относительно К, больше, чем это же расстояние, измеренное в системе К, в которой оба события одновременны. Рассчитаем расстояние l¢АВ.
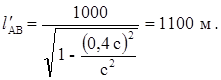
Моменты времени, в которые в системе К¢ наблюдатель зафиксирует события А и В, также могут быть найдены из преобразований Лоренца:
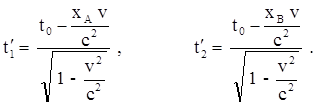
Тогда
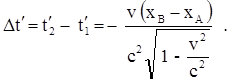
Видно, что события А и В в системе отсчета К¢ не являются одновременными. Если xB > xA и система К¢ движется в положительном направлении оси X, как и задано в условии, то t2¢ - t1¢ < 0, то есть событие В происходит раньше, чем событие А. Рассчитаем Dt¢.
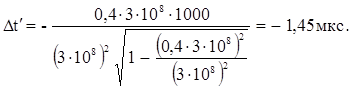
То есть событие В, зафиксированное наблюдателем в системе К¢, опережает событие А на 1,45 мкс.
Ответ: l¢АВ = 1100 м; Dt¢ = - 1,45 мкс.
