Алгоритм вычисления коэффициента ранговой корреляции Кендалла

1. Вычислить ранги объектов выборки объема n по двум признакам X и

Y :

X	x1	x2	…	xn
Y	y1	y2	…	yn

2. Определить числа Ri

( i =1, 2, ..., n −1) – количества рангов, расположенных

правее

yi и больших

yi .

Определение 10.5. Выборочным коэффициентом ранговой корре-

ляции Кендалла называется число, определяемое по формуле:

4(R1+ R2 +...+ R 1 )

τв =

n(n −1)

n− −1.

Замечание. Коэффициент Кендалла имеет те же свойства, что и коэф-

фициент Спирмена.

Для того чтобы проверить на уровне значимости α гипотезу

H 0 о том,

что

τв = 0 , при конкурирующей гипотезе

H1 :τв ≠ 0 , используют критерий

Tкр.

= zкр.

2(2n +5) ,

9n(n −1)

где

zкр.

– корень уравнения

Φ(z кр. )=

1−α

2

(находится по приложению 2).

Если

τв <Tкр. , то нет оснований отвергать гипотезу

H 0 , т.е. ранговая

корреляционная связь в генеральной совокупности не является значимой. В

противном случае гипотезу

H 0 отвергают, т.е. между признаками X и Y

имеется значимая корреляционная связь в генеральной совокупности.

Пример 10.2. Исследовалась зависимость между затратами магазинов на рекламу X (ден. ед.) и объёмом проданной продукции Y (шт.). Было об- следовано 10 однотипных магазинов. Результаты представлены в таблице:

X
Y

Найдите коэффициенты ранговой корреляции Спирмена и Кендалла.

Решение. Запишем вначале выборку в порядке ухудшения качества X .

Ранги xi
X
Y

Запишем теперь Y в порядке ухудшения качества. Получим таблицу.

Y
Ранги yi

Найдем выборочный коэффициент корреляции Спирмена:

ρв =1− 6⋅

103 −10

((1−1)2 +(2− 6)2 +(3− 2)2 +(4− 3)2 +(5− 5)2 +(6− 7)2 +

+(7− 4)2 +(8− 9)2 +(9−10)2 +(10−8)2 )= 0,794.

Значит, связь между признаками в выборке достаточно тесная.

Вычислим теперь выборочный коэффициент корреляции Кендалла.

yi
Ri										–

Тогда

τв =

4⋅(9+ 4+ 7+ 6+ 4+3+3+1+ 0)

10⋅9

−1= 0,64.

Значения вычисленных коэффициентов ранговой корреляции показыва- ют, что между затратами магазинов на рекламу и объёмом проданной про- дукции имеется существенная связь.

Теоретические вопросы и задания

1. Какие шкалы называются порядковыми? номинальными?

2. Сформулируйте алгоритм проверки независимости двух признаков с по-

мощью критерия

χ2 .

3. Для чего используются коэффициенты ранговой корреляции Спирмена и

Кендалла?

4. Каков алгоритм вычисления коэффициентов ранговой корреляции Спир-

мена и Кендалла? Как проверить их на значимость?

Задачи и упражнения

1. При изучении спроса на различные виды транспорта трёх категорий пас- сажиров: рабочих, служащих и домохозяек – получены следующие ре- зультаты:

Y X	Автобус	Маршрутка	Трамвай
Рабочие
Служащие
Домохозяйки

Определите наличие или отсутствие статистически значимой связи между

социальным статусом пассажиров и выбором используемого транспорта.

Оцените степень тесноты связи с помощью показателей Пирсона, Крамера и Чупрова.

2. Три арбитра оценили мастерство 10 спортсменов, в итоге были получены три последовательности рангов.

xi
yi
zi

Определите пару арбитров, оценки которых наиболее согласуются между собой, используя коэффициент ранговой корреляции Спирмена.

3. При приёме на работу семи кандидатам было предложено два теста. Ре-

зультаты тестирования (в баллах) приведены в таблице.

Тест	Кандидат
№ 1
№ 2

Вычислите ранговые коэффициенты корреляции Спирмена и Кендалла

между результатами тестирования по двум тестам и на уровне

оцените их значимость.

α = 0,05

Домашнее задание

1. При изучении предпочтения в выборе мест проведения отпуска у трёх ка-

тегорий отпускников получены следующие результаты:

Y X	Горные курорты	Исторические города	Морские курорты
Предприниматели
Творческие работники
Менеджеры

Определите наличие или отсутствие статистически значимой связи между категорией отпускников и предпочитаемым выбором места отдыха.

2. Специалисты двух фирм ранжировали 10 факторов по значимости их влия-

ния на ход технологического процесса. В итоге была получена таблица:

А
В

Определите с помощью коэффициентов Спирмена и Кендалла, насколько согласуются мнения специалистов двух фирм. Проверьте значимость ко-

эффициентов на уровне значимости

α = 0,01.

Занятие 11. Проблема размерности. Многомерные методы оценивания и статистического сравнения

Понятия оценивания и статистического сравнения могут быть перенесе- ны и на случай многомерной генеральной совокупности (многомерной слу- чайной величины).

Пусть из p -мерной генеральной совокупности

( X1 , X 2 ,..., X p )

сделана

выборка объёмом n . Полученные данные представим в виде матрицы:

⎛ x11

⎜

⎜ x21

X = ⎜

x12

x22

...

...

x1n ⎞

⎟

x2n ⎟

⎟.

⎜ M M

O M ⎟

x

⎜

⎝ p1

x p 2

...

⎟

x

T

pn ⎠

Точечной оценкой вектора

µ = (µ1 , µ2

,..., µp )

генеральных средних (ма-

тематического ожидания p -мерной генеральной совокупности) является

вектор выборочных средних

X = ( x1 , x2

T

,..., x p )

соответствующих компо-

1 n

нент, т.е.

xi = ∑ xij

n

j =1

( i =1, 2, ..., p ).

Точечной оценкой генеральной ковариационной матрицы S является

выборочная ковариационная матрица Sв

– квадратная матрица порядка p ,

s

ij

элементами

2 которой являются выборочные ковариации пар соответст-

1 n 2

вующих компонент, т.е.

sij = n ∑( xik − xi )( x jk − x j ) . На практике

sij

удобно на-

k =1

n

2

ходить по формуле

sij = ∑xik ⋅ x jk − xi ⋅ x j = xi ⋅ x j − xi ⋅ x j .

n

k =1

Часто при решении практических задач в качестве оценки ковариацион-

ной матрицы используют «исправленную» ковариационную матрицу

Sˆв

= n ⋅

n −1

S в .

Замечание. На практике матрицы Sв

мулам:

и Sˆв

удобно находить по фор-

1 T ˆ 1 T

Sв = n ⋅U ⋅U ,

Sв = n −1⋅U ⋅U ,

где U – матрица порядка

p× n

центрированных значений вариант:

uij

= xij

− xi .

Очень часто размерности исследуемых признаков различны. В таких случаях переходят к значениям так называемых нормированных признаков:

xij − xi

zij = . Это равносильно переходу от ковариационной матрицы

sij

Sв ис-

ходных признаков к их корреляционной матрице

Rв , элементы которой

rij

=

sii

sij

⋅ s jj

. При этом матрицу

Rв удобно находить по формуле:

где

Z = (zij ).

R = 1 ⋅ Z ⋅ Z T ,

в n

Определение 11.1. Доверительной областью некоторого парамет-

ра многомерной генеральной совокупности называется случайная область,

которая с вероятностью γ , называемой надёжностью, содержит неиз-

вестное значение этого параметра.

Доверительной областью с надёжностью γ для вектора µ генеральных

средних p -мерной генеральной совокупности, имеющей многомерное нор-

мальное распределение, при условии, что ковариационная матрица S извест-

на, является p -мерный эллипсоид, задаваемый неравенством

( X − µ )T S −1 ( X − µ ) ≤ 1 ⋅ χ 2 (1 − γ ; p) ,

n

где значение

χ2 (1 − γ; p)

находится по таблице приложения 5.

Если же ковариационная матрица неизвестна, то оценкой будет эллипсо-

ид, задаваемый неравенством

(X − µ)T Sˆ−1 (X

− µ)≤

p(n −1) ⋅ F(1− γ; p; n − p),

n(n − p)

где значение

F (1− γ; p; n − p)

находится по таблице критических точек рас-

пределения Фишера16 (приложение 6), которое иногда также называют распределением Фишера-Снедекора17.

16 Рональд Эйлмер Фишер (1890 – 1962) – английский статистик, биолог и генетик.

17 Джоржд Уоддел Снедекор (1881 – 1974) – американский математик и статистик.

Пример 11.1. Имеются следующие данные о сменной добыче угля на

одного рабочего –

X1 (т) и уровне механизации работ –

X 2 (%):

№ смены
X1
X 2

Найдите вектор выборочных средних, выборочные ковариационную и корре-

ляционную матрицы, а также доверительную область для вектора генераль-

ных средних с надёжностью γ

= 0,95.

Решение. Найдем средние по каждой переменной:

x1 =

x2 =

3+ 6 + 7 + 4 + 3 +1+ 2 + 3+ 4 + 5

2+ 5 + 5 + 2 + 4 + 3+ 3+1+ 2 + 4

=3,8;

=3,1.

Дисперсии и средние квадратические отклонения переменных

X1 и

X 2 :

2 2 2

s11 = D( X 1 ) = x1

− x1

2

= 2,96 ,

s11 =

D( X1 ) =1,72 ;

s22 = D( X 2 ) = x2

− x2

=1,69 ,

s22 =

D( X 2 ) =1,3 .

Ковариация переменных

X1 и

X 2 :

s12 = x1 x2 − x1 ⋅ x2 =1,32 .

Коэффициент корреляции

X1 и

X 2 :

s

2

12

1,32

0,59

r12 =

s11 ⋅s22

= = .

1,72⋅1,3

Итак, вектор выборочных средних, выборочные ковариационные (неис-

правленная и исправленная) и корреляционная матрицы имеют вид:

⎛3,8 ⎞

⎛2,96

1,32 ⎞

ˆ ⎛3,29

1,47 ⎞

⎛ 1 0,59 ⎞

X = ⎜ ⎟ ,

3,1

Sв = ⎜1,32

⎟,

1,69

Sв =⎜1,47

⎟,

1,88

Rв =⎜0,59 1 ⎟.

⎝ ⎠ ⎝

⎠ ⎝ ⎠ ⎝ ⎠

Найдем теперь доверительную область для вектора генеральных средних

µ = (µ1; µ2

)T . Обратная матрица для

Sˆв имеет вид:

ˆ 1 ⎛

1,88

−1,47⎞

⎛ 0,47

−0,37⎞

S−1 = ⋅ ⎜

⎟ = ⎜ ⎟ .

Тогда

в 4,02

⎝−1,47

3,29 ⎠

⎝− 0,37

0,82 ⎠

⎛ 0,47

− 0,37 ⎞⎛3,8 − µ ⎞

( X − µ)T Sˆ −1 ( X

− µ) = (3,8 − µ1

3,1 − µ2 )⎜

⎟⎜ 1 ⎟ =

⎝− 0,37

2 2

0,82

⎠⎝3,1 − µ2 ⎠

= 0,47µ1

+ 0,82µ2

− 0,73µ1µ2 −1,29µ1 − 2,30µ2 + 6,00 .

По таблице

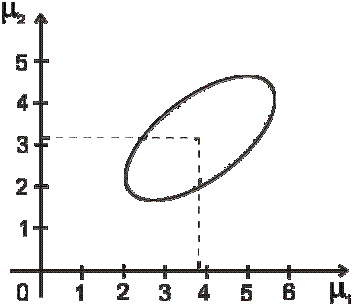
F (0,05; 2; 8) = 4,46 . Таким образом, вектор µ заключён в эллипсе

(рис. 11.1), который задаётся неравенством

2 2

x

(µ1 − 0,8µ2 −1,4)

1,42

+ (µ2 −3,1)

1,32

≤1.

Рис. 11.1

Определение 11.2. Две многомерные генеральные совокупности на- зываются однородными, если они имеют одинаковые законы распределения с одними и теми же параметрами.

Пусть из p -мерных генеральных совокупностей X и Y , имеющих нор-

мальные распределения, сделаны выборки объёмом nx

и n y

соответственно.