Ранговый коэффициент корреляции Кендалла

Другим широко используемым ранговым коэффициентом является ранговый коэффициент корреляции Кендалла, определяемый соотношением

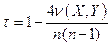, (4.50)

где n(X,Y) – минимальное число обменов соседних элементов последовательности X, необходимое для приведения ее к упорядочению Y.

Из (4.6) сразу следует, что при совпадающих ранжировках X и Y t=1 (т.к. n(X,Y)=0), а при противоположных – t=–1 (т.к. при X=n–Y+1 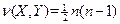). Можно показать, что во всех остальных случаях .

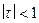Вычисление t связано с необходимостью подсчета величины n и, следовательно, является более трудоемким, чем вычисление коэффициента Спирмена r. Однако, во-первых, коэффициент Кендалла обладает некоторыми преимуществами по сравнению с коэффициентом Спирмена, главные из них: а) относительно большая продвинутость в исследовании его статистических свойств и, в частности, его выборочного распределения; б) возможность его использования и в частной («очищенной») корреляции рангов; в) большие удобства его пересчета при добавлении к n статистически обследованным объектам новых, т.е. при удлинении анализируемых ранжировок.

Во-вторых, можно воспользоваться рекомендациями, упрощающими подсчет числа n как при ручном, так и при машинном счете. Так, при ручном счете оказывается полезным известный факт тождественного совпадения величины n(X,Y) и I(X,Y) – числа инверсий, т.е. числа расположенных в неодинаковом порядке пар элементов последовательностей X и Y.

Для удобства подсчета инверсий ранжируем значения первой последовательности в порядке возрастания. Значения второй последовательности – в порядке, соответствующим значениям первой последовательности. Для каждого ранга второй последовательности определяем число следующих за ним рангов R_i, меньших его величин. Суммарную величину обозначим через

.

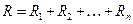Выборочный коэффициент ранговой корреляции Кендалла определится формулой

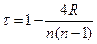. (4.51)

Убедимся, что в случае «полной прямой зависимости» признаков:

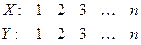
правее y_i нет рангов, меньших y_i; поэтому все R_i=0. Тогда R=0 и, следовательно, t=1. В случае «обратной зависимости» признаков:

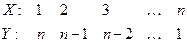
правее y_i имеется (n–1) рангов, меньших y_i; поэтому R₁=n–1. Очевидно, что R₂=n–2, R₃=n–3, ..., 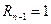. Следовательно

.

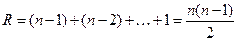Подставив это значение в (4.7), получим t=–1.

Найдем ранговые коэффициенты Кендалла в примерах 4.7 и 4.8.

Для примера 4.7:

Проекты	Ранги	Ri
R1	R2
I
II
III
IV
V
VI
VII
VIII
IX
X
Итого

Вычисления по формуле (4.7) дают:

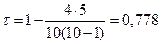
(напомним, что коэффициент Спирмена в этом примере был равным 0,915).

Для примера 4.8:

№ банка	Ранги	Ri
Rx	Ry
Итого

Вычисления по формуле (4.51) дают:

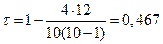
(напомним, что коэффициент Спирмена в этом примере был равным 0,588).

Если совокупность значений по исследуемому признаку содержит связанные ранги, то коэффициент корреляции вычисляется по формуле

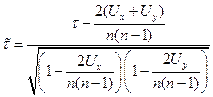, (4.52)

где

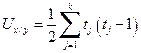, (4.53)

t_j – число одинаковых рангов в j-м ряду.

Для примера 4.7:

Участники	А	Б	В	Г	Д	Е	Ж	З	И	К
1-й судья	1,5	1,5							9,5	9,5
2-й судья

Установить, насколько объективны оценки судей, т.е. насколько тесна связь между оценками.

Участники	Ранги	Ri
Rx	Ry
А	1,5
Б	1,5
В
Г
Д
Е
Ж
З
И	9,5
К	9,5
Итого

Вычисления по формуле (4.51) дают:

.

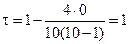Найдем поправочные коэффициенты U_x и U_y. При вычислении U_x имеем: А и Б – два объединенных ранга, Д, Е, Ж – три объединенных ранга и И, К – два объединенных ранга. Таким образом,

.

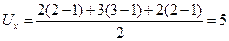Аналогично вычисляем U_y:

.

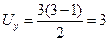В результате получаем

.

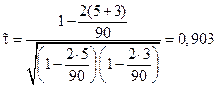(напомним, что коэффициент Спирмена в этом примере был равным 0,956).

ЛЕКЦИЯ 3 59

Глава 4. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ 59

§4.1. Многомерные случайные величины 59

4.1.1. Функция распределения двумерной случайной величины 59

4.1.2. Числовые характеристики двумерной случайной величины 60

4.1.3. Коэффициент корреляции и его свойства 61

4.1.4. Функция регрессии 62

4.1.5. Двумерное нормальное распределение 63

§4.2. Статистическая оценка коэффициента корреляции 64

4.2.1. Корреляционные зависимости. Основные задачи корреляционного анализа 64

4.2.2. Точечная оценка коэффициента корреляции 66

4.2.3. Значимость коэффициента корреляции 69

4.2.4. Интервальная оценка коэффициента корреляции 70

Дополнение 1. Корреляционное отношение и его свойства 72

Дополнение 2. Ранговая корреляция 74