Закон Ома для участка цепи с источником ЭДС

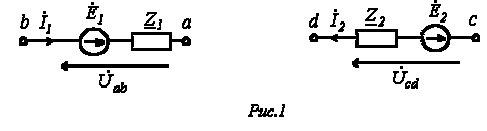Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.

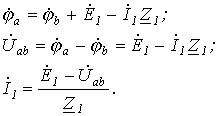
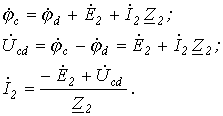
Объединяя оба случая, получим

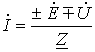(1)

или для постоянного тока

.

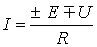(2)

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

Основы символического метода расчета цепей
синусоидального тока

Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности.

Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.

Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.

1. Первый закон Кирхгофа в комплексной форме:

.

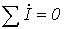(3)

2. Второй закон Кирхгофа в комплексной форме:

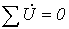(4)

или применительно к схемам замещения с источниками ЭДС

.

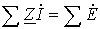(5)

3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:

§ первый закон Кирхгофа:

. ;

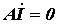(6)

§ второй закон Кирхгофа

.

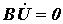(7)

Пример.

Дано:

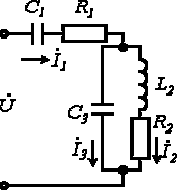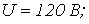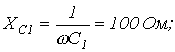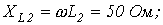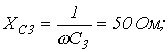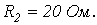Определить:	1) полное комплексное сопротивление цепи ;
2) токи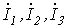
Рис. 2

Решение:

1. .

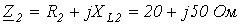2. .

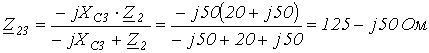3.

.

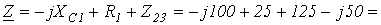
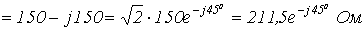4. Принимая начальную фазу напряжения за нуль, запишем:

.

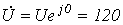Тогда

.

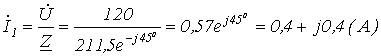5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то

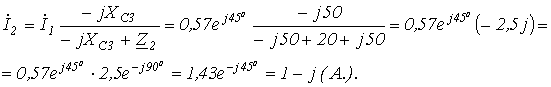
6. .

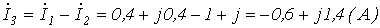7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме

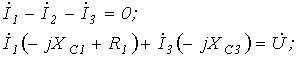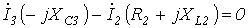или после подстановки численных значений параметров схемы

Специальные методы расчета

Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может быть сокращено, если воспользоваться специальными методами расчета, к которым относятся методы контурных токов и узловых потенциалов.

Метод контурных токов

Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых 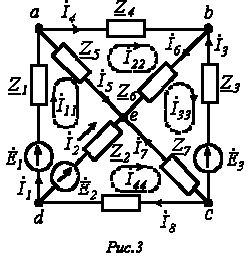контуров, т.е. числу ветвей связи графа 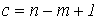. Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно 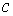и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми. Их выбор облегчает использование топологических понятий дерева и ветвей связи.

Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.

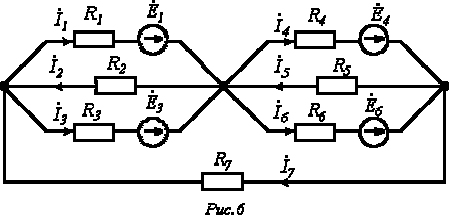
Пусть имеем схему по рис. 3.

Выразим токи ветвей через контурные токи:

;

; ;

; .

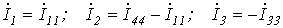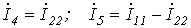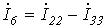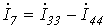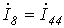Обойдя контур aeda, по второму закону Кирхгофа имеем

.

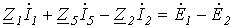Поскольку ,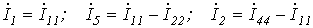

то

.

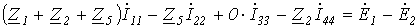Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:

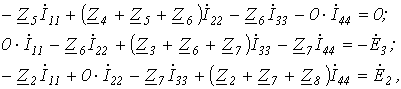
совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.

Однако данная система уравнений может быть составлена формальным путем:

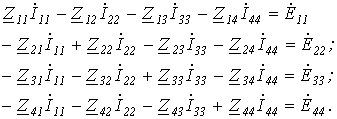
При составлении уравнений необходимо помнить следующее:

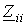- сумма сопротивлений, входящих в i-й контур;

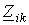- сумма сопротивлений, общих для i-го и k-гоконтуров, причем ;

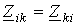члены на главной диагонали всегда пишутся со знаком “+”;

знак “+” перед остальными членами ставится в случае, если через общее сопротивление 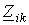i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;

если i-й и k- й контуры не имеют общих сопротивлений, то ;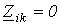

в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.

В нашем случае, для первого уравнения системы, имеем:

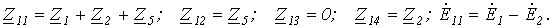
Следует обратить внимание на то, что, поскольку 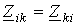, коэффициенты контурных уравнений всегда симметричны относительно главной диагонали.

Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току .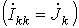

Метод узловых потенциалов

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно 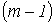, т.е. числу ветвей дерева .

Пусть имеем схему по рис. 4, в которой примем .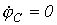

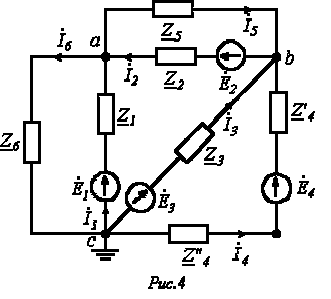Допустим, что 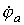и 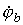известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС

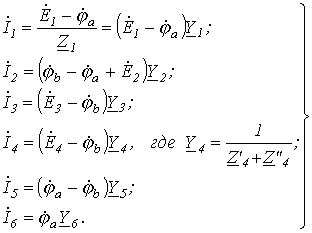
Запишем уравнение по первому закону Кирхгофа для узла а:

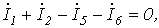
и подставим значения входящих в него токов, определенных выше:

.

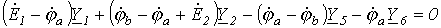Сгруппировав соответствующие члены, получим:

.

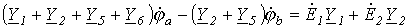Аналогично можно записать для узла b:

.

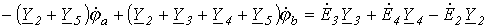Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:

1. В левой части i-гоуравнения записывается со знаком “+”потенциал 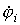i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей 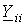ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал 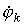соседних узлов, каждый из которых умножен на сумму проводимостей 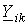ветвей, присоединенных к i-му и k-му узлам.

Из сказанного следует, что все члены 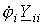, стоящие на главной диагонали в левой части системы уравнений, записываются со 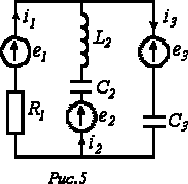знаком “+”, а все остальные – со знаком “-”, причем 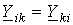. Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2. В правой части i-гоуравнения записывается так называемый узловой ток 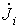, равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.

Лекция N 6