Закон Ома для участка цепи

Основополагающий закон, связывающий разность потенциалов U на концах проводника и силу тока в нем, имеет вид:

.

Данное соотношение получило название закон Ома для участка цепи и является обобщением экспериментальных данных. Здесь R – характеристика электрических свойств провода, называемая электрическим сопротивлением.

Согласно данной формуле, сопротивление в системе СИ должно измеряться в единицах В/А (Вольт делить на Ампер), которые имеют специальное название – Ом.

Более универсальной величиной, определяющейся только веществом, является удельное сопротивление. С помощью однородного провода длиной L и площадью поперечного сечения S получим связь между сопротивлением проводника R и его удельным сопротивлением :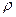

.

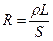Удельное сопротивление проводников растет с увеличением температуры по закону:

,

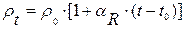позволяющему вычислить удельное сопротивление при температуре t ( 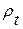) по известному удельному сопротивлению при t=0 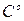( 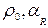– табличные величины, определяющиеся материалом провода).

Для однородного провода, в разных точках поперечного сечения которого скорость переноса заряда одинакова, можно получить связь плотности тока с электрическим полем. Поделим формулу закона Ома на S:

.

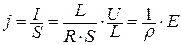Величину, обратную удельному сопротивлению, называют удельной проводимостью: 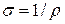. Если учесть, что направление тока совпадает с направленным движения положительных зарядов, а они движутся в направлении напряженности приложенного электрического поля, то можно записать закон Ома в локальной (дифференциальной) форме:

.

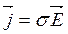Читается закон так: плотность тока в веществе пропорциональна напряженности электрического поля.

Закон Джоуля - Ленца

Какая энергия выделяется в проводящем веществе при протекании по нему электрического тока? Ответ на этот вопрос можно получить из анализа закона Ома для участка цепи.

Предположим, по проводнику с сопротивлением R протекает ток I. Какая тепловая мощность выделяется в проводнике? Запишем закон Ома в виде:

,

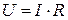где U – работа электрических сил, которую они совершают над зарядом 1 Кулон, протекающим по проводнику.

Совершение работы, как известно из механики, приводит к увеличению энергии. Но заряды в проводнике не увеличивают скорость движения, иначе бы сила тока возрастала со временем. На что же тратится работа электрических сил? На нагревание проводника. Следовательно, при протекании по проводнику заряда в 1 Кулон в проводнике выделяется в количество тепла 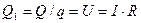. Чтобы получить тепловую мощность надо умножить величину 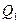на заряд, протекающий за 1 секунду, т.е. на силу тока I : P= 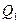I. Проделав эти несложные вычисления, получим:

.

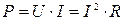Это выражение – закон Джоуля – Ленца для участка цепи.

Тепловая мощность выделяется в каждой точке проводника. Величина мощности, выделяющейся в единице объема проводника, называется объемной плотностью тепловой мощности :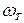

.

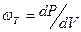Поделив полученное уравнения Джоуля – Ленца для участка цепи на объем проводника LS и используя закон Ома в локальной форме для объемной плотности тепловой мощности, получим:

.

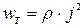Данное соотношение получило название закон Джоуля-Ленца в локальной (дифференциальной) форме. Формула позволяет вычислить энергию, выделяющуюся в единицу времени в единичном объеме проводника (в системе СИ в Дж/(м с)).