Объемное напряженное состояние

В общем случае напряженного состояния на гранях элементарного
параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов тензора напряжений. В силу закона парности касательных напряжений независимыми являются только шесть из них.

Вычислим напряжения на произвольной площадке ABC с вектором нормали ν в окрестности произвольной точки О (см. рис. 7.7). Обозначим направляющие косинусы вектора нормали ν к площадке ABC величинами:

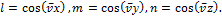
Проекции полного напряжения 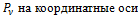, действующего на площадке АВС, обозначим 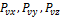. Для их определения составим уравнения равновесия четырехгранника, выделенного координатными плоскостями и плоскостью АВС в окрестности произвольной точки нагруженного тела (рис. 7.8):

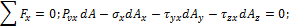
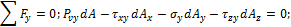
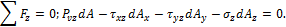
Площади граней элементов связаны между собой зависимостями:

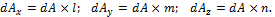
Учитывая это, получим:

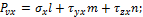
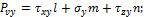
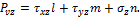
Нормальные напряжения найдем, составив сумму проекций на направление нормали:

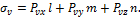
Полное напряжение на площадке:

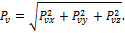
Касательное напряжение на площадке:

.

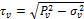Определение главных напряжений.

Пусть площадка АВС (рис. 7.8) – главная, а нормаль к ней 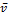совпадает с главной осью. Касательные напряжения на этой грани отсутствуют, а нормальное напряжение совпадает с полным. Проекции этого напряжения на координатные оси равны:

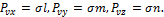
Учитывая выражение для 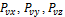, получим:

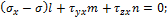
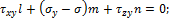
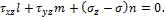
Эти равенства можно рассматривать, как однородную систему линейных алгебраических уравнений относительно l, m и n.

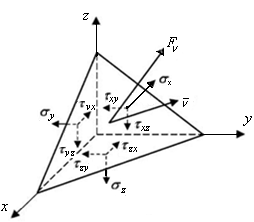
Рис. 7.8. Схема площадки для определения

главных напряжений

Так как направляющие косинусы связаны соотношениями
l + m + n = 1, нулевое решение этой системы невозможно. Нулевое решение системы возможно только в том случае, когда определитель, составленный из ее коэффициентов при неизвестных, обращается в нуль, т. е.

.

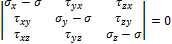Раскрыв этот определитель, получим кубическое уравнение относительно главного напряжения :

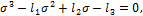
где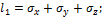

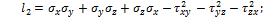
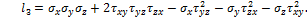
В силу симметрии определителя относительно главной диагонали, соответствующее ему кубическое уравнение имеет три действительных корня, три главных напряжения: .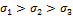

Главные напряжения в точке нагруженного тела не зависят от выбора системы координат. Поэтому

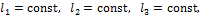
и называют их соответственно первым, вторым и третьим инвариантами тензора напряжений. Их можно представить в виде:

;

;

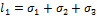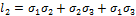В случае объемного напряженного состояния напряжения также можно представить графически. Если рассмотреть наклонные площадки, параллельные одному из главных напряжений, то для них справедливы формулы для плоского напряженного состояния. Из рис. 7.9 видно, что напряжение σ₃ не влияет на величину напряжений σ_α и τ_α, действующих на площадке, параллельной σ₃. Тогда напряжения на таких площадках можно представить графически, построив круг Мора на главных напряжениях σ₁ и σ₂. Аналогично можно представить графически напряжения на наклонных площадках, параллельных σ₁ и σ₂, как показано на рис. 7.10. Однако точки, расположенные на этих трех кругах, не исчерпывают всех наклонных площадок в точке нагруженного тела.

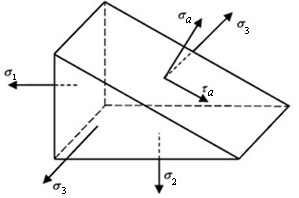
Рис. 7.9. Схема наклонной площадки при объемном

напряженном состоянии

Можно показать, что площадкам общего положения соответствуют точки на плоскости, лежащие в заштрихованной области между тремя кругами Мора. Точки, являющиеся вершинами этих кругов, соответствуют площадкам, наклоненным под углом 45^о к соответствующим главным площадкам.

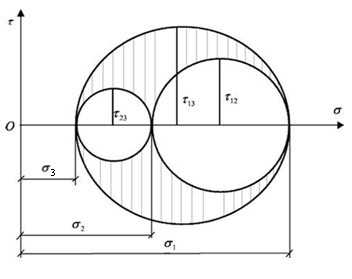
Рис. 7.10. Круги Мора для определения

касательных напряжений

Касательные напряжения на этих площадках равны радиусам кругов Мора и определяются формулами:

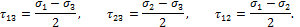
Максимальное касательное напряжение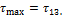

Деформированное состояние

Под действием внешних сил элементы конструкций и машин изменяют свои первоначальные размеры и форму. Эти изменения характеризуются деформациями и перемещениями тела. Перемещения упругих тел могут быть двух видов: а) перемещения как абсолютного твердого тела; б) перемещения отдельных точек тела, обусловленные деформациями материала. В механике материалов рассматриваются конструкции, в которых возникающие в них перемещения вызваны деформациями тела.

Для исследования деформированного состояния рассмотрим элемент ABCD (рис. 7.11), который после деформации тела перешел в состояние А^′B^′C^′D^′. Переход от начального состояния в конечное может быть осуществлен за счет изменения длины сторон (без изменения углов между ними) и за счет изменения углов (без изменения длин).

Пусть до деформации длина элемента АВ была равна dx, а АС – dy, угол между ними равен 90°, и ориентированы они в направлении осей Ох и Оу соответственно (рис. 7.12). Пусть после деформации точки А, В и С заняли положение А^′, В^′, С^′.Перемещения точки А в направлении оси Ох равно u, оси Оу – v, а перемещения точек В и С соответственно:

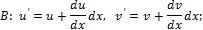
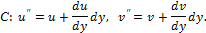
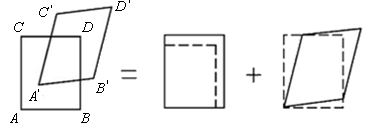
Рис. 7.11. Схема деформации элемента твердого тела

Тогда линейные деформации элементов АВ и АС определяются в виде:

.

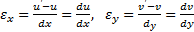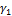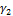Угловые деформации, т. е. изменение углов и (рис. 7.12), равны:

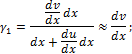
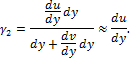
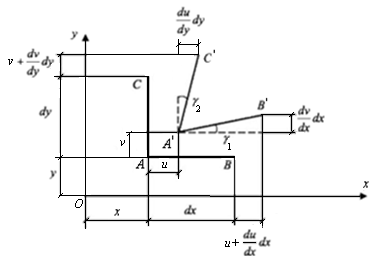
Рис. 7.12. Схема для определения линейных

и угловых деформаций элемента

Угол сдвига между элементами АВ и АС:

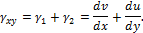
При выводе этих соотношений учитывалось, что перемещения и углы поворота малы, т. е.

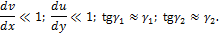
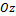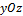Аналогично линейные деформации в направлении оси z и углы сдвига в плоскостях x и определяются по формулам:

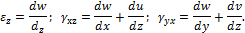
Таким образом, деформированное состояние характеризуется величинами 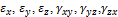, а выражения, связывающие их с компонентами вектора перемещений u, v, w, называются соотношениями Коши.

Часто при исследовании деформаций необходимо определить линейную деформацию в направлении, составляющем угол 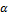с осью Ох. Рассмотрим отрезок АВ, который деформируетcя в плоскости хОу и занимает положение 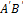(рис. 7.13). Компоненты вектора перемещения точки A в направлении осей Ох и Оу равны u, v и точки В:

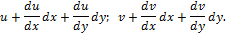
Длина отрезка АВ до деформации равна ds, а после деформации:

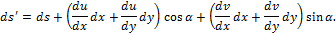
Тогда деформация отрезка АВ в направлении, определяемом углом 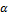, равна:

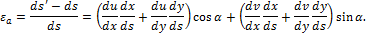
Учитывая, что

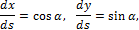
из соотношения Коши получим:

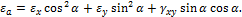
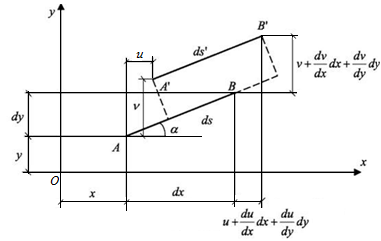
Рис. 7.13. Схема для определения деформации

элемента в направлении угла α

Если заменить 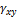на 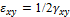, то эта формула будет полностью совпадать с выражением для 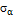. Таким образом, деформация в точке характеризуется тензором деформаций:

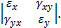
Как и тензор напряжений, его можно привести к диагональному виду:

где 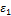и 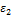– главные деформации.

Аналогично объемная деформация в точке определяется тензором деформаций, который можно представить в общем или диагональном виде:

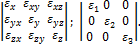
Вычислим относительно объемную деформацию тела. Для этого рассмотрим элементарный параллелепипед. Размеры сторон его до деформации равны dx, dy, dz. После деформации их размеры равны 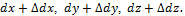Начальный объем 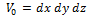, а после деформации:

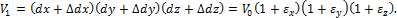
Раскрыв скобки и учитывая, что деформации малы, т. е. пренебрегая произведениями 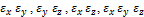, найдем относительное изменение объема:

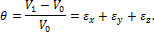
Таким образом, 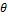является первым инвариантом тензора деформаций.

Обобщенный закон Гука

Приведенные выше формулы теории напряженного и деформированного состояния применимы как для упругих, так и для неупругих тел. Для решения контактных задач необходимо знать количественные зависимости между напряжениями и деформациями. Рассмотрим их для случая линейно-упругих, изотропных тел.

Выделим из деформированного тела элементарный куб, к граням которого приложены главные напряжения 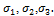Применяя принципы независимости действия сил, будем считать, что на выделенный элемент действуют только напряжения 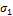, т. е. 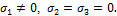Тогда он будет находиться в линейном напряженном состоянии. На основании закона Гука для линейного напряженного состояния имеем:

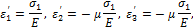
если 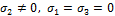, то

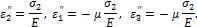
Аналогично, когда 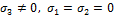, то

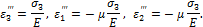
Полные линейные деформации в направлении 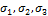равны:

.

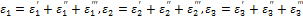Подставляя в последние выражения деформации, выраженные через напряжения, получим:

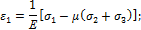
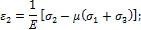
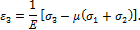
Для плоского напряженного состояния одно из напряжений (например, 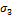) равно нулю, тогда:

;

;

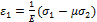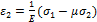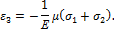
Полученные формулы называются обобщенным законом Гука для объемного и плоского напряженного состояния.