Интегрирование выражений, содержащих тригонометрические функции

1. Интегралы вида 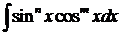, где m,n – целые.

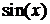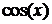Основная задача нахождения таких интегралов сводится к понижению степени или . Для этого можно воспользоваться тригонометрическими формулами приведения.

а). Пусть одно из m и n нечетное, m=2p+1. 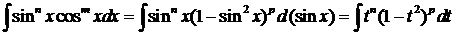. Воспользуемся формулами , ,

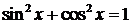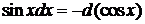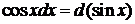
Пример 8.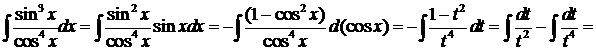

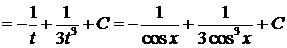
б). Пусть m, n - четные неотрицательные.Тогда воспользовавшись формулами: 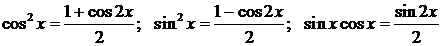(*), получим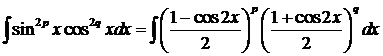

Тогда указанный выше прием а) не приводит к цели и в этом случае, предпочтительней прием, основанный на применении формул(*), а именно пусть m=2k, n=2l, и k>lk=r+l, тогда .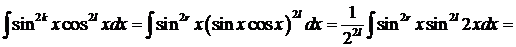

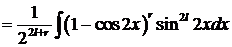Применяя формулу бинома Ньютона и затем перемножая, мы получим сумму интегралов того же вида 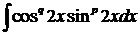, но с показателями, меньшими первоначальных. Те из них, в которых хотя бы один из показателей p и q оказывается нечетным, вычисляются приемом а). Интегралы, в которых оба показателя p и q четные могут быть вычислены с помощью многократного применения формул(*).

Пример 9. .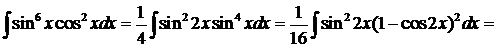

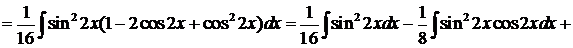
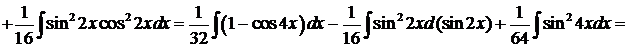
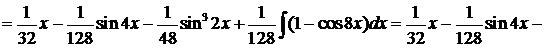
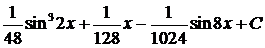2.Интегралы вида 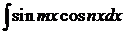, , 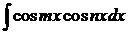, 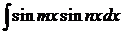где .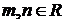

Подынтегральные функции легко приводятся к сумме первых степеней синусов и косинусов с помощью известных формул тригонометрии.
, , .

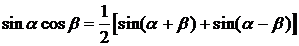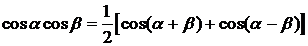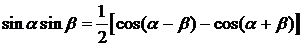Пример 10.

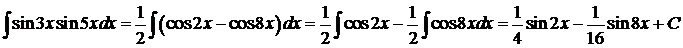Пример 11 .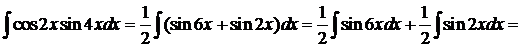

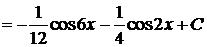Существует подстановка, которая позволяет интегрировать любые выражения, содержащие 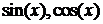. Об этом говорит следующая теорема.

Теорема 8.Интегралы вида 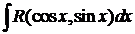всегда берутся в конечном виде. Для их выражения, кроме функций, встречающихся при интегрировании рациональных функций, нужны лишь еще тригонометрические функции.

Подстановка 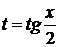называется универсальной, т.е. любое выражение, содержащее 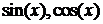при помощи этой подстановки интегрируется до конца.

Пример 12. .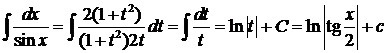

Замечание. Возможны случаи, когда цель может быть достигнута с помощью более простых подстановок:

1. Если функция R(cosx, sinx) не изменяется при одновременной замене sinx на –sinx; cosx на –cosx, то удобна подстановка x=tgx(x=ctgx), где 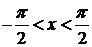, т.е.R(cosx,sinx)=R(-cosx,-sinx) . Итак,

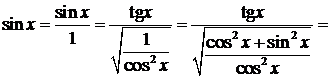
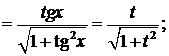
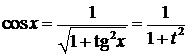. Таким образом, .

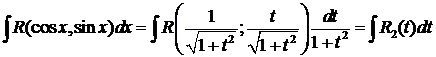2. Если при замене sinx на –sinx подынтегральная функция изменяет знак. Т.е. R(cosx, -sinx)=-R(cosx,sinx), то рационализация достигается заменой , , .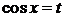

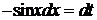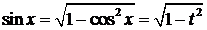
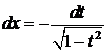3. Если при замене cosxна –cosxR(cosx,sinx)меняет знак, то рационализация достигается подстановкой , ,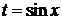

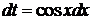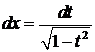
Примеры решений типовых заданий.

Пример 35. Вычислить .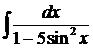

Решение. Введём замену переменной 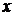. Пусть ,

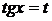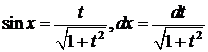, тогда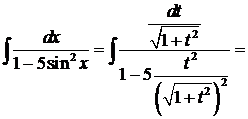 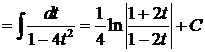. Перейдя от переменной 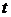обратно к 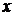, получим, что исходный интеграл равен .

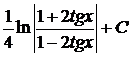Пример 36.Вычислить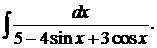

Решение. Воспользуемся подстановкой 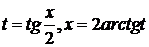. Тогда, 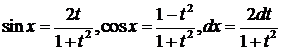.Значит, .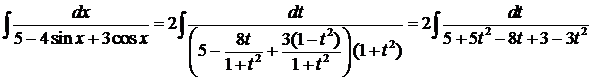

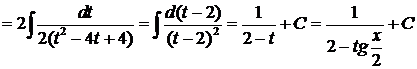Пример 37.Вычислить .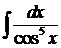

Решение. Воспользуемся заменой переменной 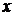. Пусть 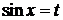. Откуда, 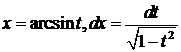. Тогда 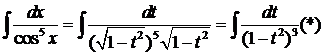. Получили интеграл от рациональной функции. Разложим его на простейшие 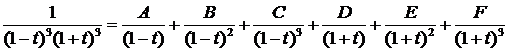. Найдя неизвестные коэффициенты, получаем следующее представление интеграла = 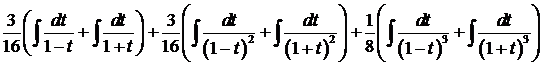. Каждый из этих интегралов является табличным и находится элементарно.

Задания на контрольную работу по дисциплине «МАТЕМАТИКА»

для студентов ЗФО

Направление 19.03.04 «ТЕХНОЛОГИЯ ПРОДУКЦИИ И ОРГАНИЗАЦИЯ ОБЩЕСТВЕННОГО ПИТАНИЯ»

Курс 1 семестр

Учебный год

РАЗДЕЛ 1. ЛИНЕЙНАЯ АЛГЕБРА

Задание № 1.

Определить, имеет ли матрицаAобратную, и если имеет, то найти ее. Результат проверить, вычислив произведениеА .

Вариант №1 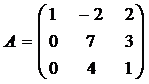, Вариант №2 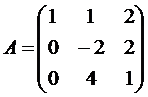, Вариант №3 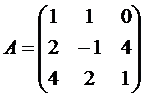, Вариант №4 ,

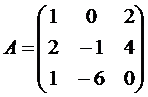Вариант №5 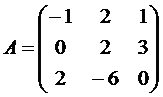, Вариант №6 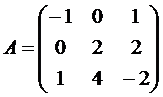, Вариант №7 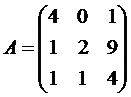, Вариант №8 ,

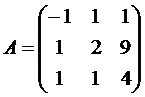Вариант №9 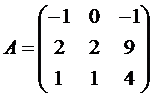,Вариант№10 ,

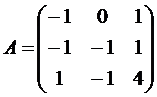Задание № 2