Неравенство и теорема Чебышева. Закон больших чисел.

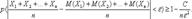Изучение статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого количества случайных величин почти утрачи-вает случайный характер и становится закономерным (иначе говоря, случайные отклонения от некоторого среднего поведения взаимно погашаются). В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Математическая формулировка этого утверждения дается в группе теорем, называемой законом больших чи

Неравенство Чебышева.

Неравенство Чебышева, используемое для доказательства дальнейших теорем, справед-ливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.

Теорема 13.1(неравенство Чебышева). p( | X – M(X)| < ε ) ≥ D(X) / ε². (13.1)

Доказательство. Пусть Х задается рядом распределения

Х х1 х2 … хп

р р1 р2 … рп

Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).

D(X) = (x1 – M(X))²p1 + (x2 – M(X))²p2 + … + (xn – M(X))²pn . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые kслагаемых. Тогда

D(X) ≥ (xk+1 – M(X))²pk+1 + (xk+2 – M(X))²pk+2 + … + (xn – M(X))²pn ≥ ε² (pk+1 + pk+2 + … + pn).

Отметим, что pk+1 + pk+2 + … + pn есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требо-валось доказать.

Теоремы Чебышева и Бернулли.

Теорема 13.2 (теорема Чебышева). Если Х1, Х2,…, Хп – попарно независимые случайные величины, дисперсии которых равномерно ограничены ( D(Xi) ≤ C), то для сколь угодно малого числа ε вероятность неравенства

будет сколь угодно близка к 1, если число случайных величин достаточно велико.

Замечание. Иначе говоря, при выполнении этих условий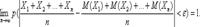

Доказательство. Рассмотрим новую случайную величину

найдем ее математическое ожидание. Используя свойства математического ожидания, получим, что

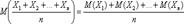Применим к 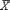неравенство Чебышева: Так как рассматриваемые случайные величины независимы, то, учитывая условие теоремы

имеем: этот результат, представим предыдущее неравенство в виде:

Перейдем

Теорема доказана.

Следствие.

Если Х1, Х2, …, Хп – попарно независимые случайные величины с равномерно ограничен-ными дисперсиями, имеющие одинаковое математическое ожидание, равное а, то для любого

сколь угодно малого ε > 0 вероятность неравенства 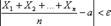будет как

угодно близка к 1, если число случайных величин достаточно велико. Иначе говоря

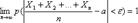
Вывод: среднее арифметическое достаточно большого числа случайных величин прини-мает значения, близкие к сумме их математических ожиданий, то есть утрачивает характер случайной величины. Например, если проводится серия измерений какой-либо физической величины, причем: а) результат каждого измерения не зависит от результатов остальных, то есть все результаты представляют собой попарно независимые случайные величины; б) измерения производятся без систематических ошибок (их математические ожидания равны между собой и равны истинному значению а измеряемой величины); в) обеспечена определенная точность измерений, следовательно, дисперсии рассматривае-мых случайных величин равномерно ограничены; то при достаточно большом числе измерений их среднее арифметическое окажется сколь угодно близким к истинному значению измеряемой величины.