Условие параллельности прямых
Прямые параллельны тогда и только тогда, когда их направляющие векторы коллинеарны. У коллинеарных векторов соответствующие координаты пропорциональны. Отсюда следует условие параллельности прямых:
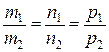 .
.
Вопросы для самопроверки
1 Записать канонические уравнения прямой в пространстве и указать геометрический смысл входящих в них параметров.
2 Записать параметрические уравнения прямой.
3 Записать уравнения прямой, проходящей через две заданные точки.
4 Записать общие уравнения прямой.
5 Записать формулу, по которой находится угол φ между прямыми.
6 Записать условия параллельности двух прямых.
7 Записать условие перпендикулярности двух прямых.
Пример 1. Найти канонические уравнения прямой 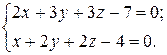
Решение
Определим координаты точки прямой. Считая, например, z = 0, получим систему уравнений
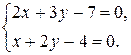
Решим данную систему уравнений.
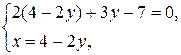
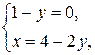
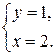
Таким образом, М(2;1; 0) точка принадлежащая прямой.
Найдем направляющий вектор прямой. По условию 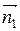 = (2; 3; 3),
= (2; 3; 3), 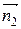 = (1; 2; 2). Тогда
= (1; 2; 2). Тогда
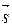 =
= 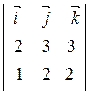 = –
= – 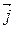 +
+ 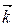 .
.
Запишем канонические уравнения исходной прямой
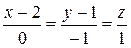 .
.
Пример 2.Составить параметрические уравнения прямой, проходящей через точку M0 (1; –2; 3) параллельно вектору 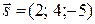 . Найти точку Р прямой, которой соответствует значение t = 2.
. Найти точку Р прямой, которой соответствует значение t = 2.
Решение
Воспользуемся формулами 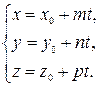
Так как в данном случае 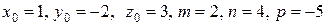 , то параметрические уравнения прямой имеют вид:
, то параметрические уравнения прямой имеют вид:
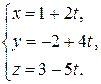
При t = 2 получим
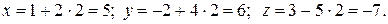
Таким образом, Р(5; 6; –7).
Задачи для самостоятельного решения
1Составить уравнение прямой, проходящей через точку М(2; 0; – 3) параллельно:
а) вектору 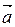 = (2; – 3; 5);
= (2; – 3; 5);
б) прямой 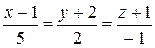 .
.
(Ответ: а) 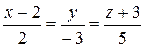 ; б)
; б) 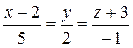 )
)
2Составить уравнение прямой, проходящей через две точки:
а) М1(1; – 2; 1), М2(3; 1; – 1);
б) М1(1; 3; – 4), М2(– 1; 2; – 4).
(Ответ: а) 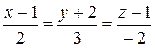 ; б)
; б) 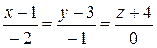 )
)
3Составить уравнение прямой, проходящей через точку А(1; – 1; – 3) параллельно прямой 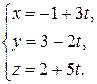 (Ответ:
(Ответ: 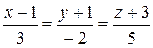 )
)
4Составить канонические уравнения прямых:
а) 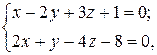
б) 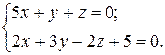
(Ответ: а) 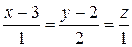 ; б)
; б) 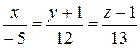 )
)
5Дан треугольник с вершинами в точках А(0; – 2; 5), В(3; 4; 1), С(1; 0; – 5). Составить уравнение медианы АD. (Ответ: 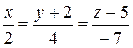 )
)
6Доказать параллельность прямых:
а) 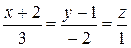 и
и 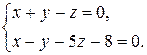
б) 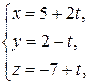 и
и 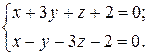
7Доказать перпендикулярность прямых:
а) 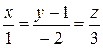 и
и 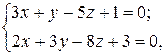
б) 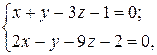 и
и 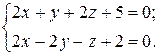
8Найти угол между прямыми:
а) 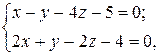 и
и 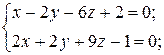
б) 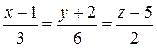 и
и 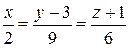 ;
;
в) 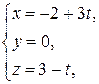 и
и 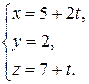
(Ответ: а) cosφ = 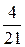 ; б) cosφ =
; б) cosφ = 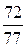 ; в) φ = 135°.
; в) φ = 135°.
9Составить уравнение прямой, проходящей через точку М(3; – 1; 2) перпендикулярно к прямым 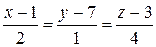 и
и 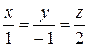 .
.
(Ответ: 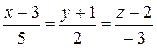 )
)
10Выяснить, пересекаются ли данные прямые, и в случае положительного ответа найти точку их пересечения:
а) 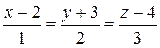 и
и 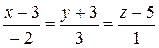 ;
;
б) 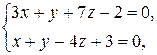 и
и 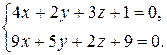
(Ответ: а) пересекаются, ( 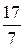 ; –
; – 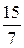 ;
; 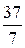 ); б) не пересекаются)
); б) не пересекаются)
Взаимное расположение прямой и плоскости в пространстве
Угол между прямой и плоскостью
Углом φ между прямой и плоскостью называется острый угол между прямой и ее проекцией на плоскость.
Пусть прямая и плоскость заданы уравнениями
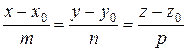 и Ах + Ву + Сz + D = 0.
и Ах + Ву + Сz + D = 0.
Для нахождения угла φ определим угол θ между направляющим вектором прямой 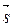 = (т, п, р) и нормальным вектором плоскости
= (т, п, р) и нормальным вектором плоскости 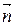 = (А, В, С) (рисунок 15). Известно, что
= (А, В, С) (рисунок 15). Известно, что
cosθ = 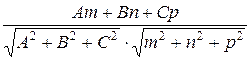 .
.
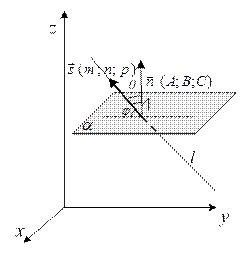
Рисунок 15 – Угол между прямой и плоскостью
Если направляющий вектор прямой выбрать так, чтобы cosθ > 0, и взять 0 ≤ θ ≤ 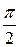 , то угол φ между прямой и плоскостью дополняет угол θ до
, то угол φ между прямой и плоскостью дополняет угол θ до 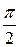 . Следовательно, cosθ = cos(
. Следовательно, cosθ = cos( 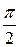 – φ) = sinφ. Поэтому
– φ) = sinφ. Поэтому
sinφ = 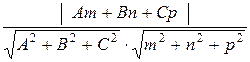 .
.
Числитель взят по абсолютной величине потому, что sinφ ≥ 0.
