Ранговый коэффициент корреляции Спирмена

Формула для коэффициента корреляции Спирмена основана на формуле парной корреляции

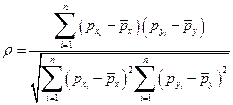, (4.45)

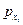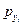где и – ранги i-й единицы совокупности по переменным x и y, соответственно; 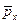и 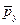– средний ранг по переменным x и y. Очевидно, что коэффициент Спирмена изменяется также как парный коэффициент корреляции, в интервале от –1 до 1.

Путем преобразований формулы (4.1) К. Спирмен еще в 1904 г. получил выражение, которое обычно используется для вычисления коэффициента корреляции Спирмена

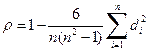, (4.46)

где d_i – разность рангов по переменным x и y для i-й единицы совокупности, n – число наблюдений.

Прямыми подсчетами нетрудно убедится, что для совпадающих ранжировок r=1 (в этом случае все значения d равны нулю); для противоположных ранжировок r=–1.

Пример 4.6. Два эксперта проранжировали 10 предложенных им проектов реорганизации НПО с точки зрения их эффективности (при заданных ресурсных ограничениях):

Проекты	I	II	III	IV	V	VI	VII	VIII	IX	X
1-й эксперт
2-й эксперт

Установить, насколько объективны оценки экспертов, т.е. насколько тесна связь между оценками.

Решение. Находим разность рангов

Проекты	Ранги	Разность рангов d=R1–R2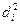
R1	R2
I			–1
II			–1
III
IV
V			–1
VI
VII			–2
VIII
IX
X
Итого

Вычисления по формуле (4.45) дают:

,

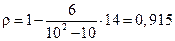что свидетельствует о существенной положительной ранговой связи между исследуемыми переменными. Следовательно, можно сделать вывод, что оценки, данные экспертами, объективны.

Пример 4.7. По группе акционерных коммерческих банков региона имеются следующие данные:

№ банка	Активы банка, млн руб.	Прибыль банка, млн руб.
		39,6
		17,8
		12,7
		14,9
		4,0
		15,5
		6,4
		10,1
		3,4
		13,4

Вычислить ранговый коэффициент корреляции Спирмена.

Решение. Для расчета коэффициента корреляции рангов предварительно выполняется ранжирование банков по уровню каждого признака:

№ банка	Активы банка, млн руб., x	Ранг по x	№ банка	Прибыль банка, млн руб., y	Ранг по y
				3.4
				4.0
				6.4
				10.1
				12.7
				13.4
				14.9
				15.5
				17.8
				39.6

Дальнейшие расчеты даны в таблице

№ банка	Ранги	Разность рангов d=Rx–Ry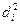
Rx	Ry
			–1
			–2
			–6
Итого

В результате получаем

,

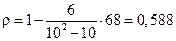что свидетельствует о умеренной положительной ранговой связи между исследуемыми переменными.

Если совокупность значений по исследуемому признаку содержит связанные ранги, то коэффициент корреляции вычисляется по формуле

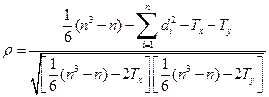, (4.47)

где

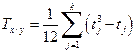, (4.48)

t_j – число одинаковых рангов в j-м ряду.

Если T_x и T_y являются небольшими относительно 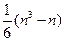величинами, то можно воспользоваться приближенной формулой (а при T_x=T_y оно точное):

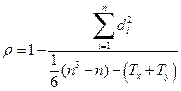. (4.49)

Правда, при этом же условии, и приближенная формула (4.2) дает хорошую точность.

Пример 4.8. На соревнованиях по фигурному катанию судьи следующим образом расположили участников соревнований:

Участники	А	Б	В	Г	Д	Е	Ж	З	И	К
1-й судья	1,5	1,5							9,5	9,5
2-й судья

Установить, насколько объективны оценки судей, т.е. насколько тесна связь между оценками.

Решение. Первый судья поделил первое место между участниками А и Б. Их объединенный ранг (1+2)/2=1,5. Участники Д, Е, Ж поделили 5, 6 и 7 места. Их объединенный ранг равен 6 и т.д.

Найдем разность рангов

.

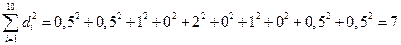Вычислим величины T_x и T_y. При вычислении T_x имеем: А и Б – два объединенных ранга, Д, Е, Ж – три объединенных ранга и И, К – два объединенных ранга. Таким образом,

.

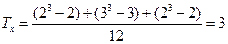Аналогично вычисляем T_y:

.

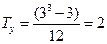В результате получаем

.

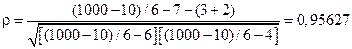По формуле (4.45) получаем следующий результат

,

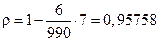а по формуле (4.58)

.

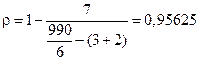Все эти результаты совпадают с точностью до второго знака.