Преобразования подынтегральных выражений.
Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика
Учебное пособие (курс лекций) 2 семестр
Для специальности 09.03.03
Прикладная информатика в экономике
Томск
ТУСУР
Электронное пособие составлено и скорректировано с учётом реального проведения лекций на ФСУ в гр. 446-1-2 весной 2017 года.
Оглавление по темам
ГЛАВА 1. ИНТЕГРАЛЫ. 5
§1. Определения и основные методы. 5
§2. Интегрирование рациональных дробей. 11
§3. Интегрирование иррациональностей и тригонометрических выражений.
§4. Определённый интеграл и его приложения.
§5. Несобственный интеграл.
§6. Кратные интегралы.
ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
§ 1. Дифференциальные уравнения 1-го порядка.
§ 2. Дифференциальные уравнения n-го порядка.
§ 3. Линейные дифференциальные уравнения n-го порядка.
§ 4. Системы дифференциальных уравнений.
§ 5. Комплексные числа, их связь с дифф.уравнениями.
ГЛАВА 3. РЯДЫ.
§ 1. Числовые ряды.
§ 2. Функциональные ряды.
§ 3. Степенные ряды.
§ 4. Ряды Тейлора и Лорана.
§ 5. Ряды Фурье.
Оглавление по номерам лекций
Лекция 1. 14.02.2017 5
Лекция 2. 21.02.2017 16
Лекция 3. 28.02.2017
Лекция 4. 07.03.2017
Лекция 5. 14.03.2017
Лекция 6. 21.03.2017
Лекция 7. 28.03.2017
Лекция 8. 04.04.2017
Лекция 9. 11.04.2017
Лекция 10. 18.04.2017
Лекция 11. 25.04.2017
Лекция 12. 02.05.2017
Лекция 13. 16.05.2017
Лекция 14. 23.05.2017
Лекция 15. 30.05.2017
ЛЕКЦИЯ № 1. 14. 02. 2017
ГЛАВА 1. ИНТЕГРАЛЫ.
Определения и основные методы.
Определение. Если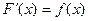 
, то 
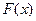называется первообразной от функции 
.
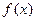Свойство.Если 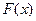первообразная, то 
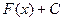(для любого 
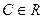) тоже является первообразной для той же самой функции .
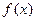Это легко доказать, действительно,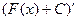 
= 
= .
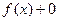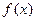Таким образом, первообразных бесконечно много, то есть, если поднять или опустить на любую высоту график 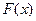, снова будет первообразная.
Свойство.Есл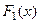и 
и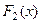 
две различные первообразные функции 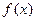, то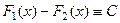 
.
Доказывается так: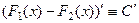 
, то есть 
.
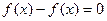Определение. Множество всех первообразных от одной и той же функции 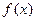называется неопределённым интегралом этой функции.
Обозначение: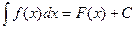 
.
Свойства линейности.
1. 
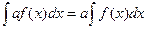
2. 
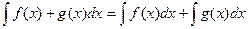
Замечание.
Для произведения свойство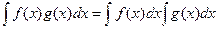 
не существует. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например 
, 
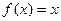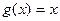. Тогда:
= 
= 
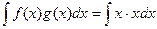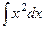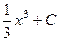, в то же время
= 
= 
.
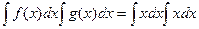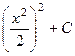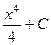Впрочем, можно даже рассмотреть 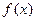произвольную, 
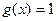. Тогда 
,
= 
.
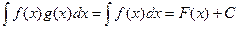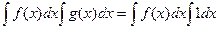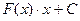Таблица основных интегралов.
( 
)
; 
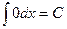
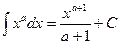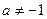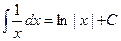
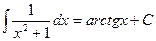
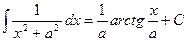
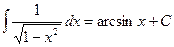
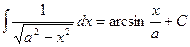
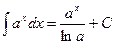
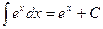
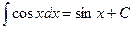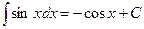
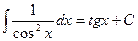
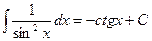
Объяснение причины возникновения модуля в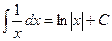 
. Функция 
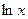существует только на правой полуоси, тогда как 
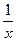имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция 
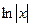является чётным продолжением 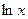на левую полуось, и именно она там является первообразной для 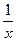при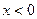 
.
Методы интегрирования.
Преобразования подынтегральных выражений.
Различные преобразования, например, арифметические (домножить и поделить, прибавить и отнять), выделение полного квадрата, разбиение многочлена на множители, преобразования по тригонометрическим формулам, и т.д. нередко помогают упростить исходное выражение, разбить его на несколько более простых слагаемых, которые уже сводятся к интегралам табличного типа. На практике рассмотрены разнообразные примеры на виды этих преобразований. Часто нужно домножить и поделить, чтобы сформировать готовое выражение, являющееся производной от известной функции. Например,
Пример. =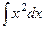 
= .
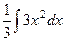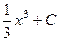Когда сформировали выражение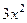 
, а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
Аналогично, допустим, что мы помним, что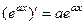 
. Тогда можно постараться сформировать готовое выражение типа 
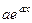внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
Пример.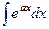 
= 
= 
.
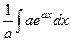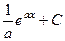Тригонометрические преобразования:
Пример. Вычислить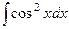 
.
Решение. Применим формулу понижения степени.
= 
= 
=
= 
.
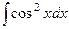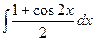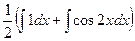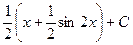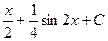Пример. Вычислить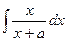 
.
Решение. =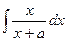 
= 
=
= 
.
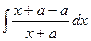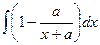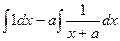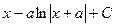Ответ. .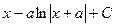
Замена переменной.
Бывают такие случаи, когда функция имеет вид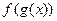 
, то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через 
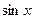или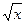 
. Делается замена на 
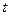, только нужно не забыть пересчитать 
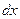, потому что 
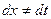, если только замена не является простым линейным сдвигом 
.
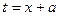Пример. Вычислить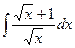 
.
Решение. Сделаем замену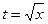 
, тогда 
, 
, 
.
= 
= 
= 
.
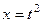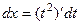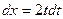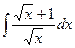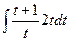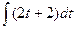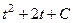Обратная замена: =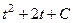 
= 
.
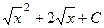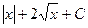Более того, область определения исходной функции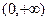 
из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: 
.
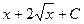Если в функции присутствуют корни разного порядка, например 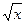и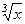 
, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от .
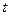Если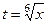 
, тогда: 
, 
.
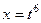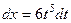Объяснение, почему все корни выразятся через целые степени :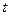
= 
,
= 
.
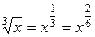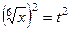
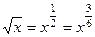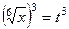