Законы Ома и Кирхгофа в комплексной форме

Введение понятий комплексного сопротивления и комплексной проводимости означает, по-существу, введение закона Ома в комплексной форме для установившегося синусоидального режима

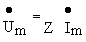или .

Комплексная амплитуда напряжения на зажимах пассивного двухполюсника равна комплексной амплитуде тока, умноженной на комплексное сопротивление двухполюсника.

Пример 1. Через зажимы двухполюсника с комплексным сопротивлением Z=40e^j30 Ом протекает синусоидальный ток i =3 Sin (314 t + 15^o) A. Определить напряжение u(t) на зажимах двухпо-люсника.

Решение.

Находя комплексную амплитуду тока 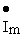=3е ^j15 и зная комплексное сопротивление двухполюсника, на основании закона Ома в комплексной форме определяем комплексную амплитуду напряжения

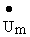=3е ^j15ґ 40e^j30=120 е ^j45 В.

Следовательно, мгновенное напряжение равно u=120 Sin (314 t + 45^o), B.

Первый закон Кирхгофа в комплексной форме : Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.

.

Поскольку каждое слагаемое в представленном выражении есть вектор, то результат есть сумма векторов. Это обстоятельсво позволяет контролировать аналитические расчеты наглядными графическими построениями-векторными диаграммами.

Пример 2: В узле ЭЦ сходятся 3 ветви с синусоидальными токам одной частоты (рис.3.3,а).

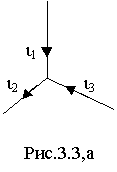
Мгновенные значения токов i ₂ и i ₃ определяются выражениями i₂= 100 Sin( 100t-45^o) и i₃= 50 Sin( 100t+30^o). Требуется определить ток i₁, пользуясь методом комплексных амплитуд.

Решение. На основании первого закона Кирхгофа в комплексной форме находим

I'_m1=I'_m2 -I'_m3 , где I'_m2=100e^-j45 , I'_m3 =50e^j30 .

Тогда

I'_m1= 100e^-j45 - 50e^j30 = 100Cos45^o - j100Sin45^o -50Cos30^o -j50Sin30^o=

=27.4-j97.5= = 101e^-j74A.

Построив вектора токов на комплексной плоскости (рис.3.3,б), убеждаемся, что сумма их действительно равна 0.

Переходя от комплекса к мгновенному значению, получим i₁= 101 Sin( 100t-74^o), А.

Второй закон Кирхгофа в комплексной форме -в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом

.

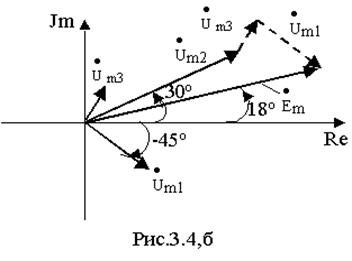
Пример 3. Известны мгновенные значения напряжений на элементах контура ( рис.3.4,а) u₁= 10 Sin( 100t-45^o) B, u₂= 25 Sin( 100t+30^o)B, u₃= 5 Sin( 100t+60^o)B. Требуется определить мгновенное значение ЭДС источника напряжения.

Решение. На основании второго закона Кирхгофа для мгновенных значений напряжений и ЭДС находим e= u₁+ u₂+ u₃.

Переходя к комплексам, получим 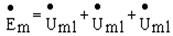, где

.

Следовательно,

=

10Cos45^o-j10Sin45^o+25Cos30^o+j25Sin30^o +5Cos60^o + j5Sin60^o =

=30.75+j9.75= 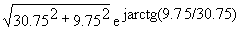= 32.3e^j18в.

Построив вектора напряжений на комплексной плоскости (рис.3.4,б ) убеждаемся, что сумма их действительно равна вектору ЭДС. Переходя от комплекса к мгновенному значению, получим e= 32.3 Sin( 100t+18^o), В.