Примеры решения индивидуалных заданий первого уровня

Задача 1. A, B - некоторые множества, ય - универсальное множество. Найдите AÇB, AÈB, A\B, B\A, A¢, B¢, A¢DB.

1) A = {2, 1, 8}, B = {9, 7, 2, 5, 1}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-10; 1], B = (-5; 20), ય = R.

Решение:

1) A = {2, 1, 8}, B = {9, 7, 2, 5, 1},ય= {1, 2, 3, 4, 5, 6, 7, 8, 9}.

AÇB = {x | xÎA и xÎB} = {1, 2};

AÈB = {x | xÎA или xÎB} = {1, 2, 5, 7, 8, 9};

A\B = {x | xÎA и xÏB} = {8};

B\A = {x | xÎB и xÏA} = {9, 7, 5};

A¢ = ય\A = {x | xÏA} = {3, 4, 5, 6, 7, 9};

B¢ = ય\B = {x | xÏB} = {3, 4, 6, 8};

Найдем A¢DB, где D - симметрическая разность.

XDY = (X\Y)È(Y\X) = (XÈY)\(XÇY).

A¢ÈB = {1, 2, 3, 4, 5, 6, 7, 9}; A¢ÇB = {5, 7, 9};

A¢DB = (A¢ÈB)\(A¢ÇB) = {1, 2, 3, 4, 6}.

2) A = (-10; 1], B = (-5; 20),ય= R.

AÇB = {x | xÎA и xÎB} = (-5; 1];

AÈB = {x | xÎA или xÎB} = (-10; 20);

A\B = {x | xÎA и xÏB} = (-10; -5];

B\A = {x | xÎB и xÏA} = (1; 20);

A¢ = ય\A = {x | xÏA} = (-¥; -10] È (1; +¥);

B¢ = ય\B = {x | xÏB} = (-¥; -5] È [20; +¥);

Найдем A¢DB, где D - симметрическая разность.

A¢ÈB = (-¥; -10] È (-5; +¥); A¢ÇB = (1; 20);

A¢DB = (A¢ÈB)\(A¢ÇB) = (-¥; -10] È (-5; 1] È [20; +¥).

Задача 2. На диаграмме Эйлера отметьте области, соответствующие данному множеству X: a) X = A\B¢Ç(B\A); b) X = A¢ \(BÈC\(AÇB)).

Решение:

1) X = A\B¢Ç(B\A).

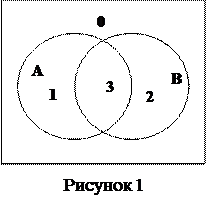
На диаграмме Эйлера пронумеруем области (рисунок 1):

Последовательно выполним опреации:

Множество B¢ состоит из областей 0, 1.

Множество A\B¢ состоит из области 3.

Множество B\A состоит из области 2.

Множество X = A\B¢Ç(B\A) пустое (области 3 и 2 не пересекаются).

Итак, X=Æ, следовательно, на диаграмме Эйлера не будет закрашенных областей.

2) X = A¢ \(BÈC\(AÇB)).

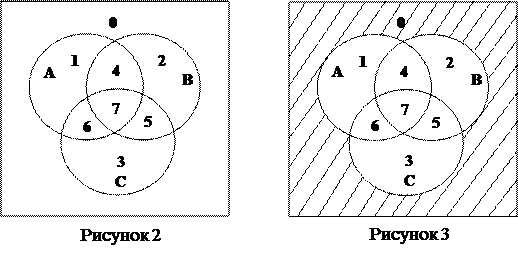На диаграмме Эйлера пронумеруем области (рисунок 2):

Последовательно выполним опреации:

Множество A¢ состоит из областей 0, 2, 3, 5.

Множество BÈC состоит из областей 2, 3, 4, 5, 6, 7.

Множество AÇB состоит из областей 4, 7.

Множество BÈC\(AÇB) состоит из областей 2, 3, 5, 6.

Множество X = A¢ \(BÈC\(AÇB)) состоит из области 0. Закрасим на рисунке область 0 (рисунок 3).

Задача 3. Упростите теоретико-множественные выражения, данные в задаче 2.

Решение:

Можно восстановить упрощенные выражения по диаграммам, составленным в пункте 2. Но для проверки можно упростить теоретико-множественные выражения, используя свойства операций над множествами.

1) X = A\B¢Ç(B\A).

A\B¢Ç(B\A) = AÇB¢Ç(BÇA¢) = AÇB¢ÇBÇA¢ = Æ

2) X = A¢ \(BÈC\(AÇB)).

A¢ \(BÈC\(AÇB)) = A¢ \(BÈCÇ(AÇB)¢) = A¢Ç(BÈCÇ(AÇB)¢)¢ =

= A¢Ç(B¢ÇC¢È(AÇB)) = (A¢ÇB¢ÇC¢)È(A¢ÇAÇB) = (A¢ÇB¢ÇC¢)ÈÆ =

= (A¢ÇB¢ÇC¢) = (AÈBÈC)¢

Задача 4. Высказывание задано формулой F, где X, Y, Z - высказывательные символы. Удалите все возможные скобки так, чтобы получилось высказывание, равносильное исходному. Затем расставьте приоритет выполнения операций и постройте таблицу истинности данного высказывания.

F º (((X & (ù Z)) « ((ù Y) V X)) ® Y)

Решение:

Удалив все возможные скобки, получим F º (X & ù Z « ù Y V X) ® Y.

В зависимости от приоритета выполнения операций введем обозначения:

F₁ º X & ù Z ; F₂ º ù Y V X; F₃ º F₁ « F₂; F º F₃ ® Y.

Построим таблицу истинности высказывания F:

X	Y	Z	ù Y	ù Z	F1	F2	F3	F

Итак, F(1,0,0) = 0 и F(X,Y,Z) = 1 для остальных наборов значений высказывательных символов X, Y, Z.

Задача 5. Упростите данную формулу F исчисления высказываний.

F º (ù X ® Y ) & ( X Ú ù Y ).

Решение:

(ù X ® Y ) & ( X Ú ù Y ) º (X Ú Y) & (X Ú ù Y) º X Ú (Y & ù Y) º X Ú 0 º X

Задача 6. P(x), T(x,y) - предикаты, определенные на множестве A. Найдите области истинности данных предикатов.

Пусть A = {0, 10, -3, 14, -1}; P(x) = «x делитель числа 30»; T(x,y) = = «x+y - четное натуральное число».

Решение: Обозначим I_P, I_T - области истинности предикатов P(x) и T(x,y) соответственно. Поскольку P(x) - одноместный, а T(x,y) - двуместный предикаты, то I_P Í A, I_T Í A´A.

В область истинности одноместного предиката P(x) входят все xÎA, для которых P(x) принимает значение “ИСТИНА”, т.е. все x, являющиеся делителями числа 30. Итак, I_P = {10, -3, -1}.

Область истинности двуместного предиката T(x,y) состоит из всех пар (x,y), для которых T(x,y) принимает значение “ИСТИНА”. В данном случае среди всех сумм по два элемента выбираем те, которые больше 0 (натуральные числа) и делятся на 2 (четные). Итак, I_T = {(0; 10), (10; 0), (0; 14), (14; 0), (10; 10), (10; 14), (14; 10), (14; 14)}.

Задача 7. Найдите область истинности предиката P(x) = « 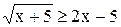», определенного на множестве R действительных чисел.

Решение: Так как P(x) - одноместный предикат, то I_P Í R.

Чтобы найти область истинности предиката P(x), определенного на множестве действительных чисел, нужно решить соответствующее неравенство относительно x.

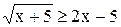
1) Если 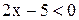, то исходное неравенство равносильно 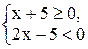Û

Û 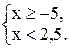Итак, xÎ[-5; 2,5).

2) Если 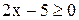, то исходное неравенство равносильно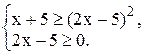

Решим первое неравенство системы:

; ; ; .

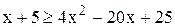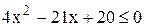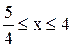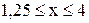Вернемся к системе неравенств: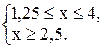

Итак, xÎ[2,5; 4].

Объединим решения, полученные в пунктах 1 и 2:

xÎ[2,5; 4] È [-5; 2,5), т.е. xÎ[-5; 4].

Задача 8. F - соответствие из A в B. Проверьте выполнимость свойств соответствия (всюду определенность, однозначность, соответствие «на», разнозначность). Выясните, является ли данное соответствие отображением.

1) A = {1, 5, 3, 7, 2}, B = {10, 2, 4}, F = {(1,10), (5,2), (2,10), (7,2), (3,2)};

2) A = B = N (множество натуральных чисел), F = {(x,y) ç y - вторая цифра числа x}.

Решение:

1) Проверим свойства соответствия.

Всюду определенность: Для любого xÎA существует хотя бы один элемент yÎB, такое, что (x,y)ÎF, т.е. F - всюду определенное соответствие.

Однозначность: Для любого xÎA существует не более одного yÎB, такого, что (x,y)ÎF, т.е. F - однозначное соответствие.

Соответствие «на»: Элемент 4ÎB не имеет прообраза во множестве A, т.е. F не является соответствием «на».

Разнозначность: Поскольку (1,10)ÎF и (2,10)ÎF, то элемент 10 множества B имеет более одного прообраза во множестве A, т.е. F не является разнозначным соответствием.

Так как F - всюду определенное однозначное соответствие, то F - отображение.

2) Проверим свойства соответствия.

Всюду определенность: Не у каждого xÎN есть вторая цифра (например, если x - однозначное число), т.е. не у каждого xÎN есть образ. Итак, F не является всюду определенным соответствием.

Однозначность: Каждое xÎN может иметь не более одной второй цифры, т.е. F - однозначное соответствие.

Соответствие «на»: Не у всякого натурального числа есть прообраз при соответствии F. Например, число 10 не может быть цифрой натурального числа. Итак, F не является соответствием «на».

Разнозначность: Например, 5 - вторая цифра натуральных чисел 256 и 3578, т.е. (256, 5)ÎF и (3578, 5)ÎF, то элемент 5 множества B имеет более одного прообраза во множестве A, т.е. F не является разнозначным соответствием.

Так как F не является всюду определенным соответствием, то F - не отображение.

Задача 9. F - отображение из A в B. Проверьте выполнимость свойств отображения (сюръективность, инъективность, биективность).

Пусть A = B = N (множество натуральных чисел), "xÎN F(x)=(x-3)²+1.

Решение:

Проверим свойства отображения.

Сюръективность: Не у всякого натурального числа есть прообраз при отображении F. Например, для числа 3 нет прообраза во множестве N, т.к. если (x-3)²+1 = 3, т.е. (x-3)² = 2, то x не может принадлежать N. Итак, F не является сюръективным отображением.

Инъективность: Поскольку (2-3)²+1=2 и (4-3)²+1=2, т.е. F(2)=2 и F(4)=2, то элемент 2 множества B имеет более одного прообраза во множестве A, т.е. F не является инъективным отображением.

Задача 10. r - бинарное отношение, определенное на множестве натуральных чисел N. Проверьте выполнимость свойств бинарного отношения (рефлексивность, симметричность, транзитивность, антирефлексивность, антисимметричность, линейность) r.

Пусть r: «"A,BÎN A r B Û произведение цифр числа A равно сумме цифр числа B».

Решение:

а) Рефлексивность: "AÎN (A r A)

Рефлексивность выполняется, если произведение цифр любого натурального числа A равно сумме цифр числа A.

Очевидно, что r - не рефлексивно, т.к., например, произведение цифр числа 12 не равно сумме его цифр (2¹3).

б) Симметричность: "A,BÎN (A r B Þ B r A)

Если из того, что произведение цифр числа A равно сумме цифр числа B, следует, что произведение цифр числа B равно сумме цифр числа A, то отношение r будет симметричным.

Отношение r не симметрично, т.к. можно подобрать контрпример. Возьмем A=23, B=33, тогда произведение цифр числа A равно 6 и равно сумме цифр числа B, но произведение цифр числа B не совпадает с суммой цифр числа A (9¹5).

в) Транзитивность: "A,B,CÎN (A r B & B r C Þ A r C)

Если из того, что произведение цифр числа A равно сумме цифр числа B и произведение цифр числа B равно сумме цифр числа C, следует, что произведение цифр числа A равно сумме цифр числа C, то отношение r будет транзитивным.

Отношение r не транзитивно, т.к. можно подобрать контрпример. Возьмем A=23, B=33, C=45, тогда произведение цифр числа A равно 6 и равно сумме цифр числа B, произведение цифр числа B равно 9 и равно сумме цифр числа C, но произведение цифр числа A не совпадает с суммой цифр числа C (6¹9).

г) Антирефлексивность: "AÎN ù (A r A)

Антирефлексивность выполняется, если произведение цифр любого натурального числа A не равно сумме цифр этого числа.

Поскольку есть такие натуральные числа (например, A=123), у которых произведение цифр совпадает с суммой цифр, то r не является антирефлексивным.

д) Антисимметричность: "A,BÎN (A r B & B r A Þ A=B)

Если из того, что произведение цифр числа A равно сумме цифр числа B и произведение цифр числа B равно сумме цифр числа A, следует, что A=B, то отношение r будет антисимметричным.

Отношение r не антисимметрично, т.к. можно подобрать контрпример. Возьмем A=123, B=321, тогда произведение цифр числа A равно 6 и равно сумме цифр числа B, произведение цифр числа B равно сумме цифр числа A, но A¹B.

е) Линейность: "A,BÎN (A r B Ú B r A Ú A=B)

Отношение r линейно, если для любых натуральных A и B выполняется хотя бы одно из утверждений: произведение цифр числа A равно сумме цифр числа B; произведение цифр числа Bравно сумме цифр числа A; A=B.

Отношение r не линейно, т.к. можно подобрать контрпример. Возьмем A=12, B=24, тогда произведение цифр числа A не равно сумме цифр числа B (2¹6), произведение цифр числа B не равно сумме цифр числа A (8¹3) и A¹B.

Итак, отношение r не рефлексивно, не симметрично, не транзитивно, не антирефлексивно, не антисимметрично, не линейно.