Образец письменного теста № 4 «Элементы аналитической геометрии на плоскости»
На выполнение работы дается 30 минут. Работа содержит 10 заданий. К заданиям №1—№9 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. В задании №10 возможно более одного верного ответа.
№1.Вектор 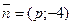 перпендикулярен прямой
перпендикулярен прямой 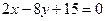 . Тогда значение p равно …
. Тогда значение p равно …
1) 1 2) 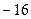 3)
3) 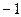 4) 16
4) 16
№2.Уравнение 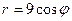 в декартовых координатах имеет вид …
в декартовых координатах имеет вид …
1) 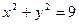 2)
2) 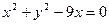 3)
3) 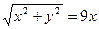 4)
4) 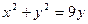
№3.Если длина отрезка АВ равна 10, то координаты начала и конца отрезка могут быть равны соответственно …
1)  2)
2) 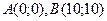 3)
3) 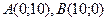 4)
4) 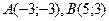
№4.Прямая проходит через точки 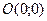 и
и 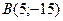 . Тогда ее угловой коэффициент равен …
. Тогда ее угловой коэффициент равен …
1) 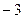 2)
2) 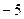 3) 3 4) 5
3) 3 4) 5
№5.Если уравнение гиперболы имеет вид 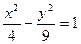 , то длина ее действительной полуоси равна …
, то длина ее действительной полуоси равна …
1) 3 2) 2 3) 4 4) 9
№6.Расстояние между точками 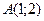 и
и 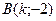 равно 5 при k равном …
равно 5 при k равном …
1) 4 2) 6 3) 10 4) 1
№7.Даны точки 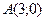 и
и 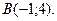 Тогда координаты середины отрезка АВ равны …
Тогда координаты середины отрезка АВ равны …
1) 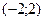 2) (1;2) 3) (4;2) 4) (2;4)
2) (1;2) 3) (4;2) 4) (2;4)
№8.Радиус окружности, заданной уравнением 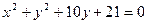 , равен …
, равен …
1) 4 2) 3 3) 1 4) 2
№9.Полюс полярной системы координат совмещен с началом декартовой системы координат, а полярная ось совпадает с положительной полуосью абсцисс. Тогда точка 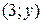 , заданная в декартовой системе координат, имеет полярный радиус
, заданная в декартовой системе координат, имеет полярный радиус 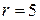 при y, равном …
при y, равном …
1) 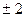 2) 2 3)
2) 2 3) 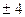 4) 8
4) 8
№10.Среди прямых 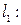
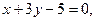
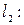
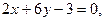
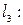

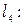
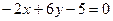 параллельными являются …
параллельными являются …
1) 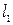 и
и 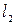 2)
2) 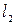 и
и 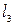 3)
3) 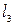 и
и 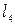 4)
4) 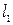 и
и 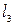
Образец РГР № 1 «Элементы линейной алгебры»
№1.Вычислить определитель.
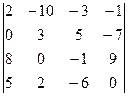
№2.Решить систему линейных уравнений 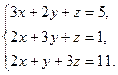
1) по правилу Крамера;
2) матричным методом;
3) методом Гаусса.
№3.Решить систему линейных уравнений 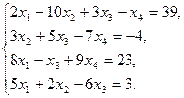 методом Гаусса.
методом Гаусса.
Теоретические вопросы для подготовки к защите
РГР №1 «Элементы линейной алгебры»
1. Определение определителей 2-ого и 3-его порядков. Свойства определителей.
2. Определения минора и алгебраического дополнения элемента определителя.
3. Правило Крамера решения систем линейных уравнений.
4. Понятие матрицы. Виды матриц.
5. Действия над матрицами.
6. Определение обратной матрицы. План нахождения обратной матрицы.
7. Решение систем линейных уравнений матричным методом.
8. Метод Гаусса решения систем линейных уравнений.
Задачи для подготовки к защите
РГР № 1 «Элементы линейной алгебры»
№1.Выполните действия:
1) 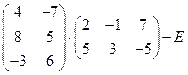 , где Е ― единичная матрица соответствующей размерности.
, где Е ― единичная матрица соответствующей размерности.
2) 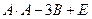 , где А=
, где А=  , В=
, В= 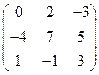 , Е ― единичная матрица.
, Е ― единичная матрица.
№2.Решите систему линейных уравнений 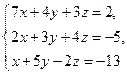
1) по правилу Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
Образец РГР № 2 «Элементы векторной алгебры»
Используйте параметры: n=2, m=3, l=4.
№1.Дано: 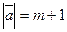 , Найти: а)
, Найти: а) 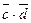 , если
, если 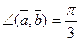 ;
;
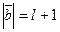 , b)
, b) 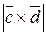 , если
, если  .
.
 ,
,
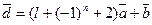 .
.
№2.Дано:  ,
,
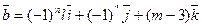 ,
,
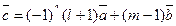 .
.
Найти длину и направляющие косинусы вектора 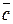 .
.
№3.Дано: А ( 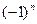 m,
m,  , 0), Найти: a) cos
, 0), Найти: a) cos 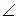 ABC;
ABC;
B ( 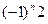 , 3,
, 3, 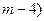 , b)
, b) 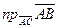
C ( 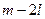 , 1, 3), c) площадь треугольника АВС;
, 1, 3), c) площадь треугольника АВС;
D (0, 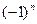 , 2). d) объем пирамиды АВСD.
, 2). d) объем пирамиды АВСD.
Теоретические вопросы для подготовки к защите
