Элементы аналитической геометрии на плоскости

Элементы аналитической геометрии на плоскости

Декартова система координат на плоскости. Уравнение линии

Для задания декартовой системы координат на плоскости определяют точку О – начало координат, пару неколлинеарных векторов, образующих базис, и единицу измерения длины. Прямые, проведенные через начало координат параллельно и сонаправленно базисным векторам, называют осями координат. Если оси перпендикулярны, то система координат называется прямоугольной. С горизонтальной осью абсцисс Ox и вертикальной осью ординат Oy. Ортонормированный базис на плоскости принято обозначать векторами 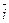для оси абсцисс и 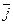для оси ординат. Тогда координатами точки M на плоскости Oxy будут проекции ее радиус-вектора на соответствующие оси.

Если 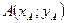, , 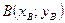то для определения координат точки 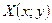, делящей отрезок в заданном соотношении 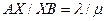, используются формулы 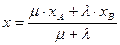, 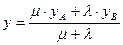. Расстояние между точками A и B определяется как .

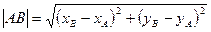Уравнением линии (кривой) на плоскости 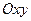называется уравнение, которому удовлетворяют координаты 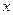и 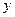каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

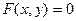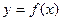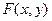В общем случае уравнение линии может быть записано в неявном виде или в явном виде , где и 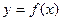– некоторые функции.

Чтобы убедиться, что точка 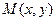лежит на данной линии 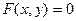, надо проверить, обращают ли координаты этой точки уравнение 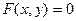в верное равенство.

Прямая на плоскости

Уравнение прямой с угловым коэффициентом

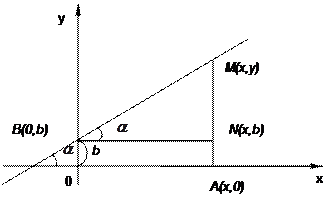Пусть прямая пересекает ось Oy в точке 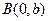и образует с осью Ox угол ( ).

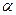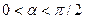Возьмем на прямой произвольную точку 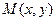. Тогда тангенс угла 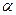наклона прямой найдем из прямоугольного треугольника :

.

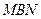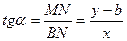Введем угловой коэффициент прямой 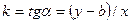, откуда получим уравнение прямой с угловым коэффициентом

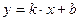(1)

1. Если 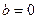, то получаем 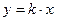– уравнение прямой, проходящей через начало координат и образующей при 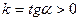острый угол с осью Ox, а при 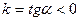– тупой угол.

2. Если 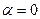, то 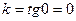, и уравнение прямой, параллельной оси Ox, имеет вид 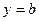, а самой оси Oy – вид .

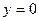3. Если 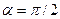, то прямая перпендикулярна оси Ox и 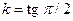не существует, т.е. прямая не имеет углового коэффициента, т.е. вертикальна и параллельна оси Oy. Предположим, что эта прямая отсекает на оси Ox отрезок, равный a. Очевидно, что уравнение такой прямой 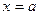, т.к. абсцисса любой точки прямой равна 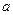, а уравнение оси Oy есть .

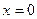Уравнение прямой, проходящей через данную точку в данном направлении (с заданным угловым коэффициентом)

Пусть прямая проходит через точку 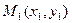и образует с осью Ox угол 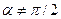. Т.к. точка 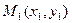лежит на прямой, то ее координаты удовлетворяют уравнению (1), т.е. .

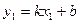Вычитая его из равенства (1), получим уравнение искомой прямой

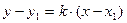. (2)

Параметрическое уравнение прямой

Обозначим коэффициент пропорциональности координат в уравнении (3) t, т.е. 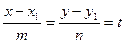. Тогда 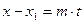, , 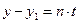откуда параметрическое уравнение прямой

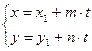(4)

Угол между прямыми

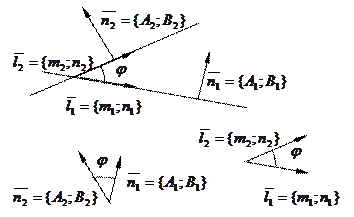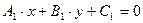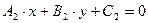Рассмотрим две прямые, заданные общими уравнениями и . Можно показать, что угол между прямыми 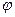(т.е. их направляющими векторам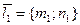и и 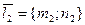) и угол между их нормалям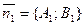и и 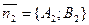равны, тогда из свойств скалярного произведения векторов нормалей найдем: .

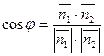Кроме того, если прямые заданы уравнениями с угловым коэффициентом, т.е. 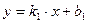, , 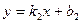то угол между ними можно определить как .

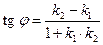Окружность

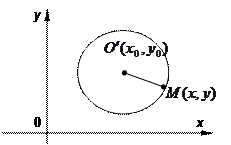Уравнение окружности радиуса 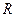с центром 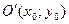имеет вид

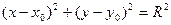. (9)

В частности, уравнение окружности с центром в начале координат 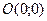имеет вид .

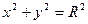Рассмотрим уравнение второй степени с двумя переменными в общем виде

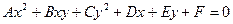, (10)

в котором 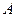, 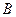и 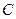не равны нулю одновременно, т.е. .

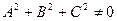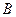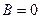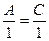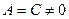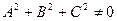Чтобы уравнения (9) и (10) представляют одну и ту же линию, коэффициент должен равняться нулю, т.е. , а все остальные коэффициенты – быть пропорциональны, в частности, , откуда (т.к. , а 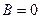). Тогда получим уравнение

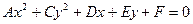, (11)

называемое общим уравнением окружности.

Поделив обе части уравнения на 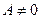и дополнив члены, содержащие 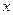и 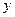, до полного квадрата, получим

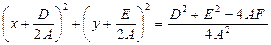. (12)

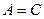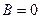Сравнивая уравнения (12) и (9), можно сделать вывод что уравнение (12) есть уравнение действительной окружности, если 1) ; 2) ; 3) 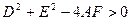. При выполнении этих условий центр окружности (12) расположен в точке 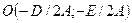, а ее радиус .

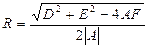Эллипс

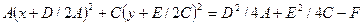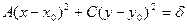Перепишем (10) в виде или , где 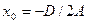; ; 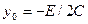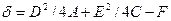. В предположении 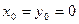уравнение кривой примет вид:

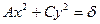. (13)

Кривая второго порядка (13) называется эллипсом (кривой эллиптического типа), если коэффициенты 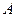и 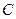имеют одинаковые знаки. Будем считать, что 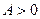и 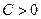(в противном случае обе части уравнения можно умножить на ( 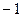)). Тогда возможны три случая:

1) 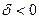– кривая (13) не имеет действительных точек;

2) 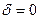– кривая (13) представляет собой одну точку;

3) 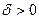– кривая (13) переписывается в виде

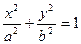. (14)

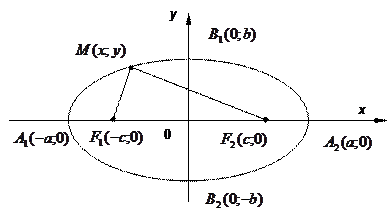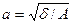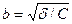Уравнение (14) называется каноническим уравнением эллипса с полуосями и . При 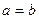уравнение (14) представляет собой уравнение окружности 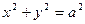. В предположении, что a>b, обозначим 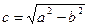, тогда точки 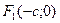и 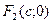называются фокусами эллипса, а отношение 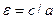– его эксцентриситетом. Эксцентриситет характеризует форму эллипса. Очевидно, что 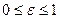, причем для окружности .

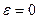Можно показать, что для любой точки эллипса сумма расстояний от этой точки до фокусов есть величина постоянная, равная 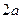. Это характеристической свойство эллипса часто принимается за его определение.

Гипербола

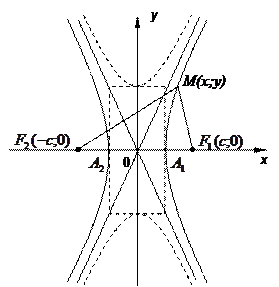Кривая второго порядка (13) называется гиперболой (кривой гиперболического типа), если коэффициенты и 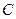имеют противоположные знаки, т.е. 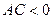. Пусть для определенности 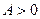, 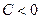. Возможны три случая.

1) 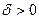соответствует гиперболе с каноническим уравнением вида

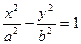, (15)

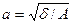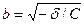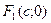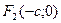где – действительная полуось, а – мнимая полуось. Фокусы гиперболы – точки и , где 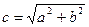, а ее эксцентриситет 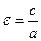принимает любые значения, большие единицы. Вершины гиперболы – точк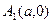и и 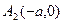. Можно показать, что для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная, равная 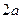: 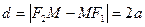. Это характеристическое свойство гиперболы часто принимают за определение гиперболы. Прямые 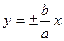, называется асимптотами гиперболы. Для равносторонней гиперболы ( 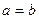) 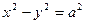асимптоты 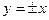взаимно перпендикулярны и представляют биссектрисы координатных углов.

2) При 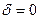уравнение кривой (15) примет вид 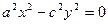, т.е. получим пару пересекающихся прямых 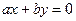и .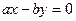

3) При 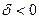получим гиперболу 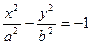с полуосям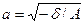и - и 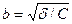, называемую сопряженной с гиперболой (15) (на рисунке она изображена пунктиром).

Парабола

Пусть в уравнении кривой второго порядка (10) 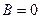, а также один из коэффициентов 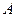или 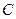равен нулю. Пусть для определенности 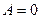, , 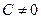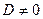тогда

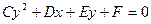. (16)

Или, после выделения полного квадрата при y: .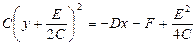

Полагая 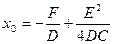, , 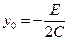, 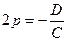получим

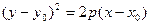. (17)

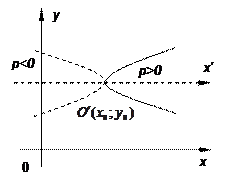Кривая (17) называется параболой, точка 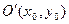– вершиной параболы, p – параметром параболы. При 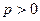ветви параболы направлены вправо, при 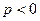- влево. Прямая 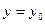является осью симметрии параболы.

Если вершина параболы находится в начале координат, то уравнение (17) принимает вид:

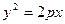. (18)

Точка 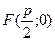называется фокусом параболы, а прямая 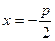- ее директрисой.

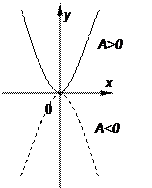Можно показать, что парабола представляет множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристической свойство параболы часто принимается за определение параболы.

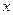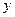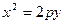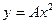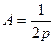Если в уравнении (18) поменять местами и , то получим - уравнение параболы с вершиной в начале координат, симметричной относительно оси ординат. Это уравнение обычно записывают в виде , где . При 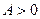ветви параболы направлены вверх, при 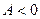- вниз.

Можно показать, что , график квадратного трехчлена 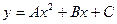есть парабола с вершиной в точке 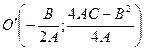и осью симметрии 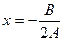, параллельной оси .

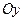Элементы аналитической геометрии на плоскости