Таблицы, выполненные средствами Microsoft Excel, с пояснениями.
КУРСОВАЯ РАБОТА
По дисциплине «Информатика» __________________________________________________
_____________
(наименование учебной дисциплины согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема:
________Построение эмпирических формул методом наименьших квадратов
Автор: студент гр. ВД-11 ___________ /Гвоздовский С.Е./
(подпись) (Ф.И.О)
Оценка:______________
Дата:________
Проверил:
Руководитель проекта _____________ /Журов Г.Н./
(подпись)
Санкт-Петербург
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»
УТВЕРЖДАЮ
Заведующий кафедрой
доц. /Маховиков А.Б./
“__” __________ 2012.
 Кафедра Информатики и компьютерных технологий
Кафедра Информатики и компьютерных технологий
КУРСОВАЯ РАБОТА
 По дисциплине: Информатика
По дисциплине: Информатика
(наименование учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
Студент группы ВД-11 Гвоздовский С.Е.

 (шифр группы) (Ф.И.О.)
(шифр группы) (Ф.И.О.)
1. Тема проекта:Использование информационных технологий для решения прикладных задач на примере построения аппроксимации функции методом наименьших квадратов.
2. Исходные данные к проекту:Вариант №11 задана таблица двух наблюдаемых переменных «X» и «Y».
3. Содержание пояснительной записки: Пояснительная записка включает в себя задание по выполнению работы, расчётные формулы, расчёт с помощью таблиц (Microsoft Exel), схему алгоритма, программу расчёта (на языке Turbo Pascal), результаты расчёта, графики, заключение, библиографический список.
4. Перечень графического материала: Представление результатов в виде графиков.
Срок сдачи законченного проекта
Руководитель работы: доцент/____________//Журов Г.Н./
(должность) (подпись) (Ф.И.О.)
Дата выдачи задания: 08.09.2012
Санкт-Петербург
Аннотация
В данной работе приводится решение задачи, которая заключается в установлении средней температуры прогрева частицы от её радиуса для различных наполнителей, с помощью табличного редактора MS Excel и языка программирования Turbo Pascal v.7.0.
Отчёт содержит: 37 страниц текста, 18 рисунков, приложения и библиографический список из 2 пунктов.
In this paper we present a solution to the problem, which is to determine the average temperature of heating the particles of the radius for different fillers, using MS Excel spreadsheet editor and a programming language Turbo Pascal v.7.0. is resulted.
The report contains: 37 pages of the text, 18 drawings, appendices and the bibliographic list from 2 points.
Оглавление:
1. Задание…………………………………………………………………………………….5
2. Введение…………………………………………………………………………………..7
3. Расчётные формулы……………………………………………………………….........9
4. Таблицы выполненные средствами Microsoft Excel, с пояснениями…………....12
5. Представление результатов в виде графиков………………………………………19
6. Получение числовых характеристик………………………………………………...21
с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ……………………………..22
7. Вычисление прогнозного значения………………………………………………......23
8. Расчёт аппроксимаций по программе в среде TURBO PASCAL 7.0……………..24
9. Вывод……………………………………………………………………………………..33
10. Список Литературы………………………………………………………………..….34
11. Приложения………………………………………………………………………….....35
Задание
1. Используя метод наименьших квадратов результаты эксперимента, представленные в виде таблицы, аппроксимировать:
а) многочленом первой степени 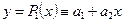 ;
;
б) многочленом второй степени 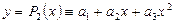 ;
;
в) экспоненциальной зависимостью 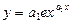 .
.
2. Для каждой зависимости вычислить коэффициент детерминированности и остаточную дисперсию на одну степень свободы.
3. Вычислить коэффициент корреляции (только в случае а).
4. Для каждой зависимости построить линию тренда.
5. Используя функцию ЛИНЕЙН вычислить числовые характеристики зависимости y от x.
6. Сравнить свои вычисления с результатами, полученными при помощи функции ЛИНЕЙН.
7. Для каждой зависимости провести оценку значимости уравнения регрессии в целом по критерию Фишера при уровне значимости α1.
8. Для каждой зависимости провести оценку параметров, входящих в уравнение регрессии, по критерию Стьюдента при уровне значимости α2.
9. Написать программу на языке Turbo Pascal.
10. Сравнить результаты работы программы с вычислениями, выполненными вручную.
11. Сделать вывод, какая из полученных формул наилучшим образом аппроксимирует результаты эксперимента.
Исходные данные (таблица 1)
При проведении эксперимента зависимость массы эксперимента установлена зависимость средней температуры прогрева частицы от её радиуса для различных наполнителей. Наполнитель NH4Cl.α1=0,05;α2=0,05.
Таблица 1
| у | х |
| 3,1 | 1,2 |
| 1,5 | 1,3 |
| 1,1 | 1,4 |
| 0,7 | 1,5 |
| 0,5 | 1,6 |
| 0,4 | 1,7 |
| 0,2 | 1,9 |
| 0,15 | 2,0 |
| 0,1 | 2,2 |
| 0,05 | 2,3 |
| 0,02 | 2,5 |
| 0,01 | 2,7 |
| 3,0 |
Введение
Цель данной курсовой работы – с помощью аппроксимации установить зависимость между экспериментальными данными, решить поставленную задачу различными способами, провести расчёты с помощью табличного процессора Microsoft Excel и среды программирования Turbo Pascal 7.0.
Аппроксимация (от латинского «approximate»-«приближаться») – приближенное описание эмпирических данных с помощью уравнений, необходима для проведения интер- и экстраполяции. Задача – найти такую функцию, выраженную аналитической формулой, чтобы она наилучшим образом описывала эмпирические данные.Наиболее часто используется метод наименьших квадратов, который позволяет найти функцию с такими параметрами, что сумма квадратов отклонений найденной функции от заданных значений функции будет минимальной.
Между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться со вторым вариантом. При выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей. Для этого и применяется аппроксимация – приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости (или ее «тренд»).
При выборе аппроксимации следует исходить из конкретной задачи исследования. Важно учитывать, насколько существенны и чем обусловлены отклонения конкретных значений от полученного тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, много параметрическое уравнение.
Таким образом, выбирая метод аппроксимации, исследователь всегда идёт на компромисс: решает, в какой степени в данном случае целесообразно и уместно «пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить зависимость сопоставляемых переменных.
Специалисты в области автоматизации технологических процессов и производств имеют дело с большим объёмом экспериментальных данных, для обработки которых используется компьютер.
При рассмотрении различных задач в этой области возникает, в частности, необходимость выявления некоторых эмпирических закономерностей, решения систем уравнений, первичной статической обработки экспериментальных данных.
Для решения многих задач, исходные данные и полученные результаты вычислений которых могут быть представлены в табличной форме, используют табличные процессоры (электронные таблицы) и, в частности, Excel. Имеется также множество инженерных задач, для решения которых требуется применить язык программирования.
В данной работе использована среда языка программирования Turbo Pascal 7.0 для основной массы расчётов, то есть для установления зависимости средней температуры прогрева частицы, электронные таблицы Microsoft Excel 2003 из пакета Microsoft Office для создания контрольного варианта и построения графиков; текстовой редактор Microsoft World 2003 для оформления отчета о проделанной работе.
При выполнении работы были использованы материалы лекций и рекомендованные источники литературы.
3.Расчётные формулы
Есть разные способы оценки суммарной ошибки аппроксимации. Чаще всего оценивают суммарную квадратичную ошибку, равную сумме квадратов отклонений эмпирических значений функции от теоретических:
Эмпирическая формула:
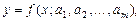 (1)
(1)
Где 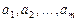 – неизвестные параметры, значения которой в точках
– неизвестные параметры, значения которой в точках 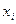 мало отличались бы от опытных значений
мало отличались бы от опытных значений 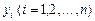 .
.
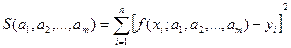 (2)
(2)
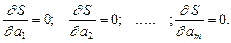 (3)
(3)
Нахождения коэффициента 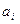 сводиться к решению системы (3)
сводиться к решению системы (3)
В случаи линейной формулы зависимости 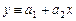 система (3) примет вид:
система (3) примет вид:
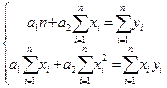 (4)
(4)
В случае квадратичной зависимости 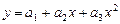 система (3) примет вид:
система (3) примет вид:
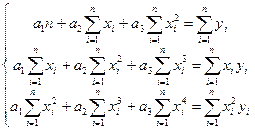 (5)
(5)
Экспоненциальная зависимость:
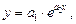 (6)
(6)
где 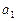 и
и 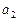 – неопределенные коэффициенты.
– неопределенные коэффициенты.
Линеаризация достигается путем логарифмирования равенства (6), после чего получаем соотношение
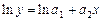 (7)
(7)
Коэффициент корреляции вычисляется по формуле:
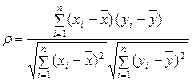 , (8)
, (8)
где 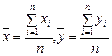 ,
, 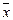 и
и 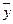 – среднее арифметическое значение соответственно по x и y.
– среднее арифметическое значение соответственно по x и y.
Коэффициент детерминированности (детерминации) определяется по формуле:
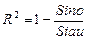 (9)
(9)
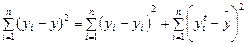 (10)
(10)
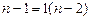
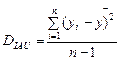 (11)
(11)
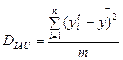 (12)
(12)
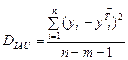 (13)
(13)
Где m-число параметров при переменных x.
Для линейной и экспоненциальной аппроксимации m=1,для квадратичной аппроксимации m=2.
Критерий Фишера определяться соотношение:
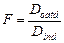 (14)
(14)
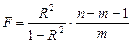 (15)
(15)
Для линейной и экспоненциальной функции формула имеет вид:
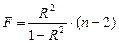 (16)
(16)
Для параболы формула F- критерия будет:
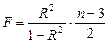 (17)
(17)
Стандартная ошибка коэффициента регрессии 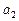 определяется по формуле:
определяется по формуле:
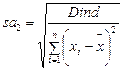 (18)
(18)
Стандартная ошибка параметра 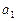 :
:
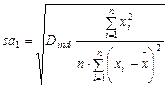 (19)
(19)
Для оценки значимости квадратичной зависимости используется аналогичный подход. Значения стандартных ошибок вычисляются по формулам:
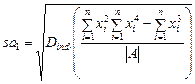 (20)
(20)
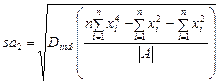 (21)
(21)
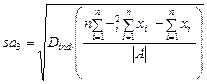 (22)
(22)
Таблицы, выполненные средствами Microsoft Excel, с пояснениями.
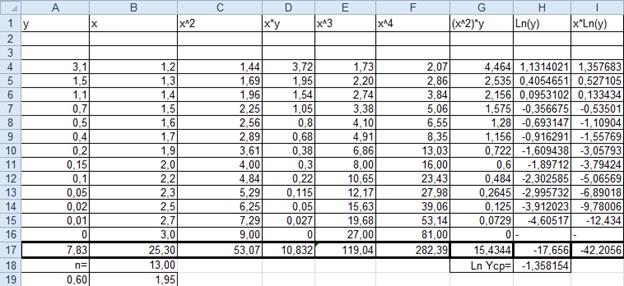
Рис.2вычисления вспомогательных сумм и средних значений.
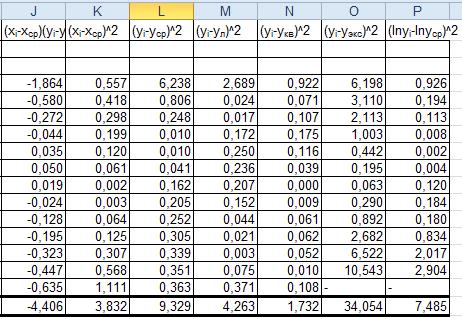
Рис.3.Вычисления вспомогательных сумм (продолжение).
Пояснения к расчётам:
Шаг 1.В ячейки A3:A16 заносим значения у
Шаг 2.В ячейки B3:B16 заносим значения x
Шаг 3.В ячейку C3 вводим формулу =B3^2
Шаг 4.В ячейки С4:С16 эта формула копируется
Шаг 5.В ячейку D3 вводим формулу B3*A3
Шаг 6.В ячейки D4:D16 эта формула копируется
Шаг 7.В ячейку E3 вводим формулу B3^3
Шаг 8.В ячейки E4:E16 эта формула копируется
Шаг 9.В ячейку F3 вводим формулу =B3^4
Шаг 10.В ячейки F4:F16 эта формула копируется
Шаг 11.В ячейку G3 вводим формулу =B3^2*A3
Шаг 12.В ячейки G4:G16 эта формула копируется
Шаг 13.В ячейку H3 вводим формулу =LN(A3)
Шаг 14.В ячейки H4:H16 эта формула копируется
Шаг 15.В ячейку I3 вводим формулу =B3*LN(A3)
Шаг 16.В ячейки I4:I16 эта формула копируется
Шаг 17.В ячейки A3:A16 заносим значения у
Шаг 18.В ячейки B3:B16 заносим значения x
Шаг 19.В ячейку J3 вводим формулу =(B3-$B$19)*(A3-$A$19)
Шаг 20.В ячейки J4:J16 эта формула копируется
Шаг 21.В ячейки K3 вводим формулу =(B3-$B$19)^2
Шаг 22.В ячейки K4:K16 эта формула копируется
Шаг 23. В ячейку L3 вводим формулу =(A3-$A$19)^2
Шаг 24.В ячейки L4:L16 эта формула копируется
Шаг 25.В ячейку M3 вводим формулу =(A3-($E$26+$E$27*B3))^2
Шаг 26.В ячейки M4:M16 эта формула копируется
Шаг 27.В ячейку N3 вводим формулу =(A3-($F$40+$F$41*B3+$F$42*B3^2))^2
Шаг 28.В ячейки N4:N16 эта формула копируется
Шаг 29.В ячейку O3 вводим формулу ==(LN(A3)-$H$18)^2
Шаг 30.В ячейки O4:O16 эта формула копируется
Шаг 31.В ячейку P3 вводим формулу =(H3-(LN($E$56*EXP($E$55*B3))))^2
Шаг 32.В ячейки P4:P16 эта формула копируется
Последующие шаги делаем с помощью автосуммирования 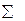
Шаг 33.В ячейку A17 вводим формулу =СУММ(A3:A16)
Шаг 34.В ячейку B17 вводим формулу =СУММ(B3:B16)
Шаг 35.В ячейку C17 вводим формулу =СУММ(C3:C16)
Шаг 36.В ячейку D17 вводим формулу =СУММ(D3:D16)
Шаг 37.В ячейку E17 вводим формулу =СУММ(E3:E16)
Шаг 38.В ячейку F17 вводим формулу =СУММ(F3:F16)
Шаг 39.В ячейку G17 вводим формулу =СУММ(G3:G16)
Шаг 40.В ячейку H17 вводим формулу =СУММ(H3:H16)
Шаг 41.В ячейку I17 вводим формулу =СУММ(I3:I16)
Шаг 42.В ячейку J17 вводим формулу =СУММ(J3:J16)
Шаг 43.В ячейку K17 вводим формулу =СУММ(K3:K16)
Шаг 44.В ячейку L17 вводим формулу =СУММ(L3:L16)
Шаг 45.В ячейку M17 вводим формулу =СУММ(M3:M16)
Шаг 46.В ячейку N17 вводим формулу =СУММ(N3:N16)
Шаг 47.В ячейку O17 вводим формулу =СУММ(O3:O16)
Шаг 48.В ячейку P17 вводим формулу =СУММ(P3:P16)
Далее вычисляем среднее значение:
Шаг 49.В ячейку B18 вводим формулу =СЧЁТ(B3:B16)
Шаг 50.В ячейку A19 вводим формулу =A17/$B$18
Шаг 51.В ячейку B19 вводим формулу =B17/$B$18
Шаг 52.В ячейку H18 вводим формулу =H17/$B$18
На рис.4 представлены расчёты для линейной аппроксимации.
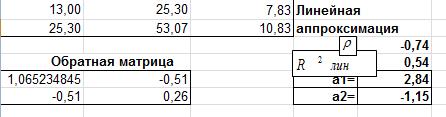
Рис.4 Фрагмент рабочего листа MS Excel для линейной аппроксимации.
Шаг 53.В ячейку A22 вводим формулу =$B$18
Шаг 54.В ячейку B22 вводим формулу =B17
Шаг 55.В ячейку A23 вводим формулу =B17
Шаг 56.В ячейку B23 вводим формулу =C17
Шаг 57.В ячейку C22 вводим формулу =A17
Шаг 58.В ячейку C23 вводим формулу =D17
Шаг 59.В ячейку A26:B27 вводим формулу =МОБР(A22:B23)
Шаг 60.В ячейку E26:E27 вводим формулу =МУМНОЖ(A55:B56;C51:C52)
Шаг 61.В ячейку E24 вводим формулу =J17/(K17*L17)^(1/2)
Шаг 62.В ячейку E25 вводим формулу =1-M17/17
Шаг 63.В ячейку B29 вводим число 4,96 (определено по a=0,05,df=1 и df2=12 в табл.П1 из приложения 1.)
Шаг 64.В ячейку B30 вводим формулу =E25*(B18/2)-(1-E25)
Шаг 65.В ячейку B31 вводим формулу =M17/(B18-2)
Шаг 66.В ячейку B32 вводим формулу =((B31*C17)/(B18*K17)^(1/2)
Шаг 67.В ячейку B33 вводим формулу =(B3/K17)^(1/2)
Шаг 68.В ячейку C30 вводим формулу =ЕСЛИ(B30>B29;»Уравнение значимо»;»Уравнение не значимо»)
Шаг 69.В ячейку D31 вводим число 2,201 (определено по a=0,05,df=1 и df2=13 в табл.П2 из приложения 2.)
Шаг 70.В ячейку D31 вводим формулу =ABS(E26)/B32
Шаг 71.В ячейку D33 вводим формулу = ABS(E27)/B33
Шаг 72.В ячейку F32 вводим формулу = =ЕСЛИ(D32>$D$31;"значим";"не значим")
Шаг 73.В ячейку F33 вводим формулу = =ЕСЛИ(D33>$D$31;"значим";"не значим")
Таким образом уравнение линейной регрессии имеет вид:
y = -1,1498x + 2,84 (23)
При этом ,согласно критерию Фишера-Снекондера, уравнение линейной регрессии (23) значимо и коэффициенты этого уравнения согласно критерия Стьюдента тоже значимы.
На рис.5 представлены расчёты для квадратичной аппроксимации.
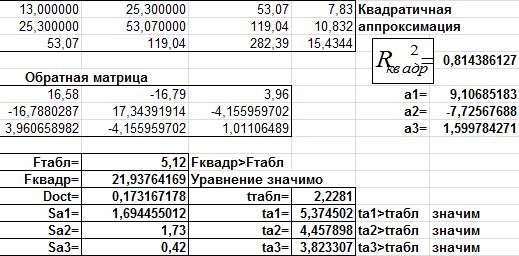
Рис.5. Фрагмент рабочего листа MS Excel для квадратичной аппроксимации.
Шаг 74.В ячейку A35 вводим формулу =$B$18
Шаг 75.В ячейку A36 вводим формулу =B17
Шаг 76.В ячейку A35 вводим формулу C17
Шаг 77.В ячейку A37 вводим формулу =B17
Шаг 78.В ячейку B34 вводим формулу =C17
Шаг 79.В ячейку B35 вводим формулу =B17
Шаг 80.В ячейку B36 вводим формулу =C17
Шаг 81.В ячейку B37 вводим формулу =E17
Шаг 82.В ячейку C35 вводим формулу =C17
Шаг 83.В ячейку C36 вводим формулу =E17
Шаг 84.В ячейку C37 вводим формулу =F17
Шаг 85.В ячейку D35 вводим формулу =A17
Шаг 86.В ячейку D36 вводим формулу =D17
Шаг 87.В ячейку D37 вводим формулу =G17
Шаг 88.В выделяем ячейки A40:C42 и вводим формулу {=МОБР(A35:C37)}
Шаг 89.В выделяем ячейки F40:F42 и вводим формулу {=МУМНОЖ(A40:C42;D35:D37)}.
Шаг 90.В ячейку F38 вводим формулу =1-N17/L17
Шаг 91.В ячейку B44 вводим число 5,12 (определено по a=0,05,df=1 и df=11 табл.П1 из приложения 1.)
Шаг 92.В ячейку B45 вводим формулу =F38*(B18-3)/2(2*(1-F38)).
Шаг 93.В ячейку B46 вводим формулу =N17/(B18-3)
Шаг 94.В ячейку B47 вводим формулу =((N17/($B$18-3))*A40)^(1/2)
Шаг 95.В ячейку B48 вводим формулу =((N17/($B$18-3))*A41)^(1/2)
Шаг 96.В ячейку B49 вводим формулу =((N17/($B$18-3))*A42)^(1/2)
Шаг 97.В ячейку С45 вводим формулу =ЕСЛИ(B45>B44;»Уравнение значимо»;»Уравнение не значимо»).
Шаг 98.В ячейку C45 вводим формулу
Шаг 99.В ячейку D46 вводим число 2,2281 (определено по a=0,05 и df=12 табл.П2 из приложения 2.)
Шаг 100.В ячейку D47 вводим формулу =ABS(F40)/B47
Шаг 101.В ячейку C48 вводим формулу =ABS(F41)/B48
Шаг 102.В ячейку D49 вводим формулу =ABS(F42)/B49
Шаг 103.В ячейку F47 вводим формулу = =ЕСЛИ(D47>$D$46;"значим";"не значим")
Шаг 104.В ячейку F48 вводим формулу = =ЕСЛИ(D48>$D$46;"значим";"не значим")
Шаг 105.В ячейку F49 вводим формулу = =ЕСЛИ(D49>$D$46;"значим";"не значим")
Таким образом уравнение квадратичной регрессии имеет вид:
y = 1,5998x2 - 7,7257x + 9,1069 (24)
Согласно критерию Фишера – Снедекора, уравнение квадратичной регрессии (24) значимо. Два коэффициента этого уравнения а2=0,891114 и а3= -7,59066E-05согласно критерия Стьюдента значимы, а третий а1=0,197806347 не значим. Таким образом квадратичная аппроксимация становиться линейной.
На рис.6 представлены расчёты для экспоненциальной аппроксимации.
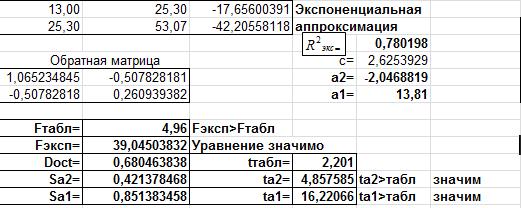
Рис.6. Фрагмент листа MS Excel для экспоненциальной аппроксимации.
Шаг 106.В ячейку A51 вводим формулу =$B$18
Шаг 107.В ячейку B51 вводим формулу =B17
Шаг 108.В ячейку A52 вводим формулу =B17
Шаг 109.В ячейку B52 вводим формулу =C17
Шаг 110.В ячейку C51 вводим формулу =H17
Шаг 111.В ячейку C52 вводим формулу = I17
Шаг 112.Выделяем ячейки А55:В56 и вводим формулу{=МОБР(А51:В52)}
Шаг 113.Выделяем ячейки E54:E55 и вводим формулу{=МУМНОЖ(А55:В56;С51:С52)}
Шаг 114.В ячейку E56 вводим формулу =EXP(E54)
Шаг 115.В ячейку E53 вводим формулу =1-P17/O17
Шаг 116.В ячейку B58 вводим формулу = B29
Шаг 117.В ячейку B59 вводим формулу =E53*(B18-2)/(1-E53)
Шаг 118.В ячейку B60 вводим формулу =P17/(B18-2))
Шаг 119.В ячейку B61 вводим формулу = (P17/(($B$18-2)*K17))^(1/2).
Шаг 120.В ячейку B62 вводим формулу =((P17*C17)/(($B$18-2)*$B$*K17))^(1/2)
Шаг 121.В ячейку C59 вводим формулу = ЕСЛИ(B59>B58;"Уравнение значимо";"Уравнение не значимо")
Шаг 122.В ячейку D60 вводим формулу =D31
Шаг 123.В ячейку D61 вводим формулу = ABS(E55)/B61
Шаг 124.В ячейку D62 вводим формулу =ABS(E56)/B62
Шаг 125.В ячейку F61 вводим формулу = ЕСЛИ(D61>$D$60;"значим";"не значим")
Шаг 126.В ячейку F62 вводим формулу = ЕСЛИ(D62>$D$60;"значим";"не значим")
Но в результате выполнения работы Экспоненциальная аппроксимация не производится
(25)
Согласно критерию Фишера- Снедекора, уравнение экспоненциальной регрессии (25) значимо. Оба коэффициента этого уравнения, согласно критерию Стьюдента, значимы.
