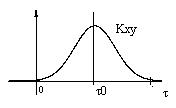
Достаточное условие эргодичности по корреляционной функции

Теорема.Если случайный процесс стационарен в широком смысле, и для процесса выполняется условие эргодичности по математическому ожиданию, то процесс является эргодическим по корреляционной функции.

Основные характеристики для эргодического процесса:

,

,

.

Стационарно связанные случайные процессы

Опр. Два случайных процесса называются стационарно связанными, если их взаимная корреляционная функция зависит только от разности аргументов .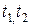

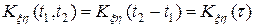
Свойство корреляционной функции стационарно связанных процессов:

.

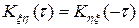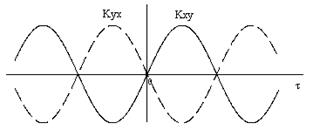
Пример. Найти корреляционную функцию стационарно связанных процессов 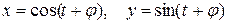, если .

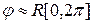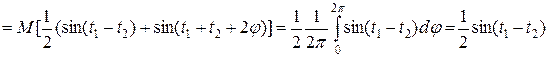
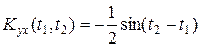
Пример. Пусть передается сигнал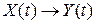

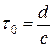
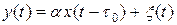
Теорема. Первая производная от стационарного случайного процесса является стационарным процессом со следующими характеристиками:

,

,

.

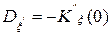Пример.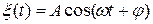

,

,

.

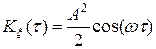Пример. , .

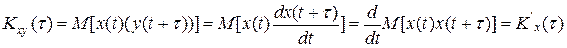
Элементы стохастического анализа {1}

Виды сходимости последовательности СВ в пространстве .

1) Последовательность СВ 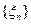называется сходящейся почти наверное к СВ 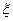( 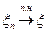), если

(за исключением быть может ).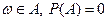

2) Последовательность СВ 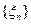называется сходящейся по вероятности к СВ 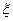( ), если

.

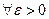
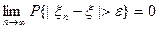3) Последовательность СВ 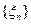называется сходящейся в среднеквадратическомсмысле к СВ 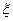( 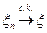), если

.

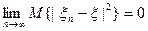Из сходимости почти наверное 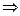сходимость по вероятности. Из сходимости в среднеквадратическом 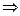сходимость по вероятности.

.

Мы рассматриваем гильбертовы СП, т.е. для которых .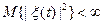

Так как существуют разные виды сходимости для СВ, то соответствующим образом существуют различные виды непрерывности для СП. Кроме того, для различных видов непрерывности (а также дифференцируемости, интегрируемости и др.) имеются соответствующие критерии, которые позволяют установить непрерывность СП (дифференцируемость, интегрируемость и др.).

СП называется непрерывным на Т, если 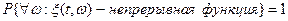. Почти все траектории непрерывного СП являются непрерывными в обычном смысле функциями. Непрерывный СП является почти наверное непрерывным в каждой точке , . Но не наоборот в общем случае.

Непрерывность в смысле сходимости по вероятности называется стохастической непрерывностью; это самый слабый из рассматриваемых видов непрерывности.

СП называется стохастически непрерывным в точке , если .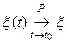

Наиболее важной является среднеквадратическая непрерывность.

СП называется среднеквадратически (с.к.-) непрерывным в точке , если .

СП называется с.к.-непрерывным на Т, если он непрерывен в каждой точке 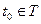.