Тест ранговой корреляции Спирмена

Для проведения теста Спирмена на наличие гетероскедостичности необходимо предварительно провести несколько процедур, а именно:

Шаг 1. Сохраним результаты построения регрессионной модели, для этого в окне Residual Analysis (Анализ остатков) выберем вкладку Save (Сохранить) и нажмем единственную доступную кнопку Save residuals & predicted (Сохранить остатки и факторы).

Рисунок 4.5 – Сохранение результатов построения регрессии (приведена часть исходного окна)

Шаг 2. В появившемся окне Select variables to save with predicted/residual scor…(Выбор переменной для сохранения с регрессорами, остатками и т.д.) выберем независимую переменную X4. После чего переходим к таблице результатов (рисунок 4.6), которая содержит независимую переменную, остатки стандартные отклонения и т.д. В дальнейшем тест Спирмена будет проводиться на ее основе.

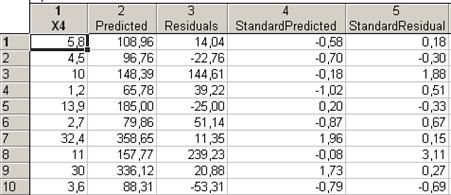
Рисунок 4.6 – Результаты оценки регрессионной модели с независимой переменной X4 (приведена часть исходного окна)

Шаг 3. Проранжируем сохраненные показатели X4 и Residuals, для этого в главном меню необходимо указать Date ® Rank ® Variables (Данные ® Ранг ® Переменные) и выбрать необходимые переменные (X4 и Residuals).

Шаг 4. В главном меню набрать Statistics ® Nonparametrics ® Correlations (Spearman, Kendall tau, gamma) (Статистики ® Непараметрические ® Корреляция).

Шаг 5. В появившемся окне нажмем кнопку Variables и сделаем установки как показано на рисунке 4.8.

Рисунок 4.7 – Окно выбора расчета непараметрических показателей корреляции

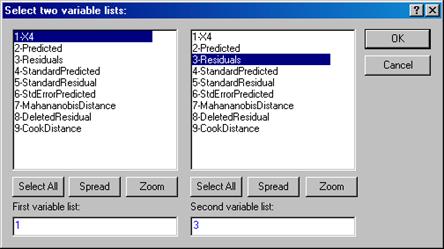
Рисунок 4.8 – Установки переменных для оценки коэффициента Спирмена

После нажатия кнопки Spearman R (коэффициент Спирмена) получим следующие результаты.

Таблица 4.8 – Результаты оценивания значения коэффициента Спирмена

	Valid N	Spearman R	t(N-2)	p-level
X4 & Residuals		-0,040	-0,231	0,819

Согласно данным, приведенным в таблице 4.8, коэффициент Спирмена получен низким и незначимым, т.е. наличие гетероскедостичности не подтверждается.

Шаг 6. Находим фактическое значение t-статистики:

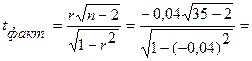-0,231

Шаг 7. t_факт сравниваем с t_табл (α/2; n-2). Если t_факт > t_табл то необходимо отклонить гипотезу об отсутствии гетероскедостичности. В нашем случае получаем |0,231|<2,0423, т.е. в данных гетероскедостичность отсутствует.

Тест Гольфельда-Квандта

Шаг 1. Для проведения данного теста в системе STATISTICA 6.0 необходимо воспользоваться исходными данными (Приложение 4А) и упорядочить совокупность по величине исследуемой независимой переменной. Для этого в главном меню выберем Date ® Sort… (Данные ® Сортировка…).

В появившемся окне Sort Options (Установки сортировки) необходимо указать переменную, по которой проводится сортировка, в нашем случае это X4 и нажать ОК.

Шаг 2. Воспользуемся модулем Multiple Regression, в стартовом окне Multiple Linear Regression в качестве зависимой переменной укажем Y в качестве не зависимой – X4. Также (в этом же окне) необходимо выбрать кнопу Select Cases (Выбор значений).

Шаг 3. В появившемся окне Analysis/Graph cases Selection conditions необходимо установить флажок в поле Enable Selection Conditions ® Specific, selected by:

После активации поля By Expression введем v0<=11, т.е. регрессия будет строиться по значениям с 1 – 11 (так как в нашем случае n»30 соответственно k=11).

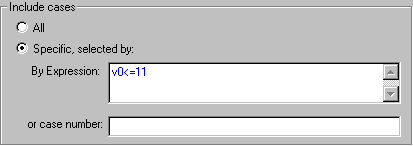
Рисунок 4.9 – Окно выбора подмножества для оценки первой регрессии (приведена часть исходного окна)

Шаг 4. Нажмем ОК®ОК. В окне Multiple Regression Results (Результаты множественной регрессии)во вкладке Advanced (Расширенные) выберем кнопку ANOVA (Overall goodness of fit) получим следующую таблицу:

Таблица 4.9 – Результаты дисперсионного анализа для модели по первым 11 наблюдениям

	Sums of Squares	df	Mean Squares	F	p-level
Regress.	546,68		546,684	0,252	0,628
Residual	19529,86		2169,985
Total	20076,55

Шаг 5. Повторяем процедуру для последних 11 значений при этом в поле By Expression необходимо указать v0>24. В результате оценивания модели получаем следующие оценки.

Таблица 4.10 – Результаты дисперсионного анализа для модели по последним 11 наблюдениям

	Sums of Squares	df	Mean Squares	F	p-level
Regress.	27948,1		27948,07	2,252	0,168
Residual	111706,5		12411,83
Total	139654,5

Шаг 4. Рассчитываем фактическое значение F-статистики Гольфельда-Квандта, для этого возьмем соответствующие значения, стоящие на пересечении строки Residual и столбца Sums of Squares, т.е. 19529,86/111706,5 = 0,175. Табличное значение F-критерия Фишера при степенях свободы v₁=8 и v₂=8 равно 3,44, т.е. получаем Fфакт<Fтабл значит, гипотеза об отсутствии гетероскедостичности принимается.