Глава 12. Начало анализа. Что же нам дает открытие s -образной кривой?
Что же нам дает открытие s -образной кривой? На самом деле — немало. Ведь это практически готовый к работе инструмент. Оказывается, строго по ее законам протекают очень многие инновационные маркетинговые процессы. Например, можно с уверенностью утверждать, что запуск новой марки будет иметь именно 5-образный характер. Причем чем более яркой и индивидуальной будет марка и чем точнее будет ограничена ниша, на которой мы выступаем, тем чище будет картина. Рассмотрим наглядный пример: российский пивной рынок, четко ограниченный сегмент лицензионного пива, причем изучаемую в настоящий момент нишу, по сути, определяют три основные конкурирующие марки: А, В и С (рис. 12.3). В момент времени ! картина складывалась таким образом: все три бренда находились на рынке (т. е. были в продаже), но только один бренд (В) продвигался своим владельцем и имел хоть какую-то известность у любителей пива. Остальные марки, не уступая ему ни в качестве, ни в имени, ни в цене, находились в положении маркетингового гомеостаза: т.е. имели свою маленькую аудиторию верных ценителей, небольшое спонтанное знание на уровне 1/ и спорадические продажи.
В момент времени t1 началась рекламная кампания по продвижению марки А1. Нетрудно видеть, что достаточно быстро (уже к моменту t3 ) спонтанное знание продвигаемого бренда легко достигло уровня лидера, слегка превзошло его (t4), но на этом рост остановился. Получается, будто мы перешли с одного естественного уровня (гомеостаза) на другой, нормальный для рекламируемых марок в данной нише. Мы выбрали довольно компактный сегмент, так что стабилизация роста знания на уровне 5-7% потребителей говорит о том, что практически все любители пива данного вида уже охвачены нашей рекламой (если перед нами, конечно, не стоит задача продвигать и растить категорию), то дальнейшая задача меняется с освоения на удержание.
Попробуем разобраться в том, насколько полезной для нас может оказаться эта функция. Понятно, что анализировать ее можно с двух позиций:
визуально- технически; аналитически.
С первым все более или менее просто: нам всего-то и надо, что построить график в осях «рекламные затраты — знание» и расположить на нем исследуемые марки (каждая из которых будет иметь координаты х — ее рекламный бюджет, у — процент ЦА, который ее знает). далее, наложив на этот график сигмовиду, можно визуально оценить: марка, лежащая ниже кривой, скорее всего, менее эффективно продвигалась, марка, лежащая выше кри-

А. Кутлалиев
А. Попов
вой, скорее всего, более результативно рекламировалась и т.д. (А. Кокор -
2001).
С аналитическим подходом несколько сложнее. На нем мы остановимся чуть более подробно. Из формулы (44) мы знаем общий теоретический вид 5-образной кривой. Различными методами (от простого перебора до построения вероятностных бумаг1) мы можем подобрать параметры нашей искомой функции. В рассматриваемом случае они оказались следующим  ,т.е. мы получили следующую формулу:
,т.е. мы получили следующую формулу:
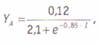 (45)
(45)
где единица в конце означает наш средний дорекламный уровень знания (около 1%, насколько мы помним). Овладение этой функцией может быт: очень важно для нас — ведь мы на практике установили зависимость меж. рекламными издержками (I) и результатом (в данном случае: уровнем знания — Y). Теперь у нас есть все основания полагать, что бренд С или какой- либо новый, если начнет рекламироваться, будет приращивать свою известность именно по формуле, равной или очень близкой к (45). Последняя оговорка довольно серьезна: ведь никто не ожидает, что бренд С прямо скопирует медиаплан и творческую идею А. Это столь же нереально, сколь ф бессмысленно: новая идея, свежий образ, нетривиальная мысль привлекают гораздо больше внимания, нежели неоднократное повторение одного в того же в разных сочетаниях.
Однако вернемся к параметрам функции. Посмотрим, от чего они зависят и каков их физический смысл. Из самых общих соображений понятия что именно в коэффициентах у, р и учитывается специфика конкретного товара или рынка, особенности региона или целевой аудитории, сила бреда или яркость идеи. Где и что учитывается в формуле, нам покажет ее математический анализ. Читатели, знакомые с ним, скорее всего знают логи параметров изучаемой функции. для них будет оправданно пропустить целях экономии времени следующие 2—З страницы. Вниманию остальных мы предлагаем рис. 12.4.
На нем изображено целое семейство нормированных s -образных кривых. В центре — нормированная сигмоида. Она построена при единичных параметрах γ,φ, и μ Для всех остальных мы чуть-чуть поиграли каким-то одним параметром, оставив два других без изменения. Таким образом, становится понятно, что параметр у, вынесенный в числитель дроби, «отвечает» за
________________
1 И снова авторы вынуждены попросить прощения у читателей, поскольку в рамка данного произведения мы совершенно не настроены детально рассматривать такие интересные но совершенно факультативные вопросы, как подбор параметров к функции распределения т.п. Благо на эту тему есть большое количество специальной литературы.
