Метод подсказки (наводящей задачи) и условия ее эффективности в исследованиях мышления

А.Н.Леонтьев

ОПЫТ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ МЫШЛЕНИЯ*

Среди психологических вопросов, относящихся к проблеме мышления, одним из наиболее важных является вопрос о том специфическом звене мыс­лительной деятельности, который придает ей отчет­ливо выраженный творческий характер.

Когда ученый или изобретатель, рабочий-раци­онализатор или учащийся стоят перед новой, впер­вые осваиваемой ими задачей, то обычно процесс решения такой задачи имеет как бы два этапа: пер­вый этап — нахождение адекватного принципа, спо­соба решения, который прямо не вытекает из ус­ловий задачи; второй этап — применение найденного уже принципа решения; вместе с тем это этап про­верки и, часто, преобразования данного принципа в соответствии с условиями конкретной решаемой задачи.

Иногда этот второй этап требует большого вре­мени и труда, но все же — это этап только дальней­шей разработки и конкретизации решения, которое в своем общем виде, т. е. именно в принципе, уже найдено, уже известно.

Другое дело — первый этап, этап нахождения самого принципа или, как иногда говорят, идеи ре­шения. Это и есть наиболее творческое, если можно так выразиться, звено мыслительной деятельности.

В психологической, и не только в психологичес­кой, литературе многократно описывались те чер­ты, которые характеризуют мыслительный процесс на этом его этапе. Главная из них как известно, со­стоит в том, что после первоначально бесплодных попыток найти решение задачи внезапно возникает догадка, появляется новая идея решения. При этом очень часто подчеркивают случайность тех обстоя­тельств, в которых происходит такое внезапное от­крытие новой идеи, нового принципа решения.

Например, один из конструкторов шагающего экскаватора бросает случайный взгляд на человека, несущего чемодан, и ему приходит в голову совер­шенно новый принцип устройства, регулирующего "шагание" этой грандиозной машины.

Что же представляет собою это, так называемое творческое звено мыслительной деятельности?

Его недостаточная изученность, естественно, создавала почву для всякого рода идеалистических психологических концепций, включая сюда и геш-тальтистскую концепцию Einsicht 'a.

Вместе с тем, надо признать, что подлинно на­учное исследование этой проблемы представляет собой задачу серьезного теоретического и практи­ческого значения.

Один из циклов исследований, ведущихся в на­стоящее время на кафедре психологии Московского

* Доклад на совещании по вопросам психологии 3—8 июня 1953 г. М., 1954.

государственного университета, мы и посвятили эк­спериментальному изучению этой проблемы.

Здесь мы имеем возможность изложить только некоторые, далеко не полные результаты этой рабо­ты, которая проводилась под нашим руководством Я. А. Пономаревым и Ю. Б. Гиппенрейтер.

Остановимся раньше на общей методике опытов.

Прежде всего нам нужно было выбрать подходя­щий тип задач.

Понятно, что мы не могли взять для экспери­мента по-настоящему значимые задачи, т. е. поста­вить испытуемого в положение, скажем, изобрета­теля или исследователя.

Мы остановились поэтому на гораздо более про­стых задачах — задачах "на догадку".

Такие задачи отличаются тем, что они требуют для своего решения только таких знаний и умений, которые заведомо имеются у испытуемых. Вместе с тем, как правило, их решение сразу не находится, т. е. условия этих задач сразу не актуализируют у испы­туемых нужных связей, вызывающих применение адекватного способа решения. Наконец, этот тип задач характеризуется тем, что если принцип реше­ния данной задачи найден, то его применение уже не представляет никакого труда и, таким образом, этап нахождения принципа решения практически совпадает со вторым этапом — этапом реализации этого решения.

Примером задач такого типа может служить следующая простейшая задача, которой пользовал­ся в своих опытах Я.А.Пономарев.

Испытуемому дается лист бумаги, на котором нарисованы четыре точки, расположенные в виде квадрата; задача состоит в том, чтобы перечеркнуть их тремя прямыми, не отрывая руки от рисунка, и вернуться к начальной точке (рис. 1).

\/

Рис. 1

Как показал опыт, взрослые люди, не знающие заранее данной задачи, быстро решить ее не могут, хотя нужные для этого элементарные геометричес­кие знания у них, несомненно, имеются. Так, если эту задачу несколько видоизменить и, например, поставить ее в следующей форме: "Опишите вокруг квадрата треугольник", то она, конечно, решается очень легко. Дело, очевидно, заключается в том, что изображение четырех точек первоначально вызыва­ет прочно закрепленное действие соединения точек

линиями, как это в подавляющем большинстве слу­чаев действительно и происходит в нашем опыте. Принцип же решения данной задачи состоит в дру­гом, а именно в том, чтобы пересечь изображенные точки, выведя линии за пределы площади, ограни­ченной этими точками.

Иначе говоря, условия данной задачи первона­чально актуализируют связи не адекватные, адекват­ные же связи не актуализируются и не вступают в новую связь — в связь с условиями именно данной задачи, хотя в других условиях, например, в услови­ях инструкции, они актуализируются очень легко.

Таков был тип задач, применявшихся в опытах.

Собственно же эксперимент заключался в том, что, взяв одну из таких задач в качестве основной, экспериментатор подводил испытуемого тем или другим дополнительным приемом к ее решению.

Эти приемы заключались в том, что испытуе­мый выполнял по требованию экспериментатора какое-нибудь упражнение или решал какие-нибудь другие задачи, которые объективно содержали в себе решение основной задачи и поэтому могли выпол­нить наводящую роль.

Таким образом, мы получили возможность про­следить, при каких же условиях опыт испытуемого наводит его на правильное решение, что, собствен­но, и выражается в так называемой догадке.

По этой методике были проведены многочис­ленные серии опытов, но мы изложим только неко­торые, наиболее простые. В одной из первых серий опытов, проведенных Я.А.Пономаревым, в качестве основной была взята описанная выше задача с че­тырьмя точками.

Вопрос был поставлен так: не будет ли решаться эта задача, т.е. не будут ли актуализироваться этой задачей адекватные связи, если они будут специаль­но закреплены в соответствующем упражнении, да­ваемом испытуемому перед тем, как он начнет ре­шать задачу.

Рис. 2

В качестве наводящих упражнений давались сле­дующие: например, испытуемый должен был мно­гократно снимать расположенные на шахматной дос­ке четыре пешки тремя ходами фигуры, которая может "брать" пешки и как ферзь, и как "дамка" при игре в шашки. При этом пешки были расположены так, что испытуемый проделывал движение, путь ко-

торого совпадал с линиями перечеркивания точек в основной задаче (рис. 2).

Или второй пример наводящего упражнения: ис­пытуемому предлагалось многократно и различным образом описывать вокруг квадрата треугольники.

Были введены и другие наводящие упражнения, описывать которые мы здесь не будем.

Какое же действие оказали эти наводящие уп­ражнения на решение предлагаемой вслед за ними задачи?

Полученные данные представляются на первый взгляд неожиданными, даже парадоксальными: ни многократное повторение отдельных упражнений, ни целые группы разных упражнений как преимуще­ственно второсигнального, так и первосигнального порядка не дали положительного эффекта: основная задача испытуемыми, предварительно проделавши­ми эти упражнения, не решалась.

Но может быть данные упражнения вообще не могут оказать наводящего действия? Это, однако, не так. Дело в том, что если эти же упражнения дать после основной задачи, оставшейся нерешенной, то их наводящее действие отчетливо сказывается при вторичном предъявлении основной задачи и она чаще всего решается сразу же.

Итак: предварительное выполнение испытуемым задания, объективно заключающего в себе способ решения основной задачи, не оказывает наводяще­го действия, и основная задача не решается.

Наоборот, выполнение такого же или аналогич­ного задания после безуспешных попыток решить основную задачу способно при определенных усло­виях приводить к ее решению "с места".

Этот факт многократно подтвержден в разных сериях опытов, на разных задачах, с помощью при­менения разных методик, включая чисто лаборатор­ную методику образования двигательных условных рефлексов, так что факт этот можно считать зако­номерным.

Анализ данного факта ставит два основных воп­роса: во-первых, вопрос о том, в силу чего задание, предшествующее основной задаче, не оказывает наводящего влияния; во-вторых, вопрос об условиях и закономерностях, характеризующих положительный эффект наводящего задания, когда оно дается после безуспешных попыток решить основную задачу.

Мы остановимся только на этом втором, в из­вестном смысле более важном вопросе.

Вопрос этот был освещен в опытах Ю. Б. Гип-пенрейтер.

Рис. 3

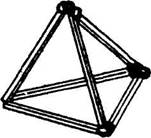
В этих опытах использовалась другая, тоже очень простая задача на догадку. Требовалось сложить из 6

спичек четыре равносторонних треугольника. Рас­кладывая спички на плоскости, это сделать невоз­можно. Чтобы решить эту задачу, надо было сложить объемную фигуру — тетраэдр, т. е. поднять спички над плоскостью (рис. 3).

В качестве наводящей применялась следующая задача: разместить на определенной площади не­сколько плоских коробок одинаковой толщины, но разных по контуру (это были обклеенные части обыч­ной картонной коробки от папирос, разрезанной на куски неправильной формы).

Части коробки своей плоской стороной на за­данной площади не размещались; чтобы сделать это, их нужно было поставить на ребро — вертикально (рис. 4).

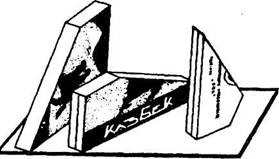
Рис. 4

После решения этой наводящей задачи испыту­емый возвращался к прежде нерешенной им основ­ной задаче, которая требовала применения того же самого принципа: отказа от построения на плоско­сти и построения треугольника в трех измерениях.

Эксперимент состоял в систематическом варьи­ровании одного из условий, в которых протекал опыт в целом, в то время как другие условия оставались постоянными. При этом положительный эффект на­водящей задачи сказывался не при всех условиях и не при всяком их соотношении, а закономерно за­висел от определенных условий и от определенного соотношения этих условий.

Какие же это условия и соотношения, от кото­рых зависит процесс наведения на решение, т. е. ко­торые вызывают у испытуемого догадку, открытие принципа, позволяющего решить основную задачу сразу, "с места"?

Прежде всего была прослежена зависимость на­водящего эффекта второй задачи от того, как испы­туемые пытались найти решение первой, основной задачи.

Нужно сказать, что среди наших испытуемых выделилась группа, которая относилась к задаче с построением треугольников из спичек без бсякого интереса. Стремление решить эту задачу у них очень скоро угасало, а некоторые из них прямо заявляли о том, что они не любят такого рода задач, что боль­ше не хотят "ломать себе голову" и т. д.

В этом случае наводящая задача, хотя и решалась ими в наиболее эффективном ее варианте, но при вторичном возвращении к основной задаче послед­няя ими и на этот раз не решалась. Противополож­ный, т. е. положительный, эффект наводящей задачи наблюдался (при прочих равных условиях) у всех

испытуемых более активных, заинтересовавшихся основной задачей, у которых интерес к ней к мо­менту перехода к наводящей задаче не угасал.

Итак, первое простейшее положение, которое может быть сформулировано на основании этих опы­тов, заключается в следующем: для того, чтобы те или иные условия оказали воздействие, наводящее на искомое решение задачи, необходимо, чтобы эта задача вызывала у человека интерес, т. е. чтобы она создавала достаточно стойкую повышенную впечат­лительность или, пользуясь выражением Ухтомско­го, "подстерегательность" к определенным раздра­жителям.

Ведь наведение и представляет собой не что иное, как один из случаев замыкания новой временной связи, а необходимым условием для этого является деятельное — и при этом избирательно деятельное состояние коры, т. е. именно наличие соответствую­щего доминантного очага возбуждения

Свое дальнейшее развитие это первое положе­ние получило в опытах с группой испытуемых, у которых желание искать решение основной задачи не угасало.

Опыты велись так: одной части испытуемых да­валась наводящая задача после безуспешных попы­ток решить основную задачу (со спичками), когда у них возникало сомнение в возможности решить та­ким способом згу задачу, но все же интерес к ней не пропадал; другой части испытуемых — в начале поисков решения, когда никакого сомнения в пра­вильности избранного ими способа решения у них еще не возникало, им говорилось, что время на ре­шение этой задачи истекло.

Как показал этот опыт, у первой подгруппы на­водящая задача всегда давала положительный эф­фект. Вторая же подгруппа испытуемых вела себя так: решив наводящую задачу и получив возмож­ность снова решать основную задачу, испытуемые продолжали свои попытки, исходящие из прежне­го принципа, т. е. продолжали строить треугольники на плоскости, причем верного решения они так и не могли найти.

Итак: для того, чтобы произошло "наведение" на правильное решение задачи, необходимо, чтобы возможности применения первого неверного прин­ципа решения были исчерпаны, но чтобы вместе с тем это не вызвало бы полного угасания поисков решения задачи.

Последняя серия экспериментов, итоги которых мы кратко изложим, состояла в том, что в ней варь­ировались опыты с наводящей задачей.

В первом варианте экспериментатор давал испы­туемому решать наводящую задачу в течение опыта несколько раз, начиная с первых же неудачных по­пыток испытуемого решить основную задачу, т. е. когда ее роль не могла еще сказаться, и до момента, который является наиболее благоприятствующим наведению на правильное решение. В этих условиях наводящая задача утрачивала для испытуемого свою новизну и переставала вызывать живую ориентиро­вочную реакцию раньше, чем наступал наиболее благоприятный момент для наведения на решение основной задачи. В результате такая "примелькавша­яся" испытуемому наводящая задача никакого дей­ствия оказать не могла.

Другой вариант состоял в том, что, при прочих равных условиях, наводящая задача резко упроща­лась путем уменьшения площади, на которой нужно было уместить коробки, так что испытуемые сразу же ставили их на ребро. Это тоже снимало ее поло­жительный эффект.

Таким образом, последнее положение, которое вытекает из опыта, заключается в следующем: наве­дение на правильное решение требует, чтобы наво­дящие обстоятельства вызывали у человека доста­точно живую ориентировочную реакцию.

Наконец, необходимо отметить следующий ха­рактерный факт, выявившийся в опытах. Оказыва­ется, обстоятельства и самый процесс наведения на решение задачи, т. е. замыкание соответствующих временных связей, не могут быть сколько-нибудь ясно отмечены самими испытуемыми. Напротив, этот момент обычно для них маскируется. Так, испытуе­мые, например, отмечают, что при повторном предъявлении основной задачи ее решение наступа­ет "как-то вдруг", а иногда дают явно неправильные указания вроде того, что задача решилась "потому, что есть такая фигура — тетраэдр".

Таким образом, изучавшееся нами звено мыс­лительной деятельности лежит вне возможности хоть сколько-нибудь правильно, даже хотя бы только описательно, представить его себе по данным само-

наблюдения, и его .изучение возможно лишь строго объективным методом. Вместе с тем, именно это звено является центральным во всякой интеллекту­альной деятельности. Оно-то и представляет собой, как мы думаем, ту "ассоциацию ассоциаций", о ко­торой упоминает И.П.Павлов, разбирая случаи "мышления в действии". Это — образование ас­социации между воздействующими условиями но­вой задачи и прежними, уже имеющимися система­ми связей, которые были выработаны в других усло­виях; актуализируясь теперь в условиях новой зада­чи, они естественно сами развиваются дальше, ви­доизменяясь соответственно требованиям этих но­вых условий.

В заключение скажем несколько слов о перспек­тиве дальнейшего исследования данного вопроса.

Мы думаем, что оно может быть продолжено, в частности, в направлении изучения творческого зве­на мыслительной деятельности в условиях усвоения, обучения.

Часто изображают этот процесс как якобы ли­шенный всякого творческого момента, всякой жи­вой догадки, открытия для себя новой идеи, что, по нашему мнению, глубоко неверно. Напротив, это очень важный момент усвоения.

С.Л. Рубинштейн

ОСНОВНАЯ ЗАДАЧА И МЕТОД

ПСИХОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ МЫШЛЕНИЯ*

Основная задача психологического исследования мышления заключается в том, чтобы, не ограничи­ваясь фиксацией внешних результатов мыслительной деятельности, вскрыть самый процесс мышления во внутренних закономерностях его протекания.

Это - генеральная линия. Она реализуется в отно­шении ряда проблем, где исследование умственной деятельности сводилось к описанию ее внешнего про­текания, к констатации фактов, в которых она выра­жается, без раскрытия внутреннего закономерного процесса, приводящего к этим фактам. Показатель­ным примером может служить проблема "переноса".

В педагогической практике учитель часто встре­чается с тем, что ученик, решивший задачу или как будто усвоивший теорему применительно к данным условиям, оказывается не в состоянии "перенести" это решение в другие условия, решить ту же задачу, как только задача предъявляется ему в видоизменен­ных условиях. Это часто встречающийся и практи­чески фундаментально важный факт. С констатации подобных фактов начинает, как известно, свое ис­следование о "продуктивном мышлении" Вертгеймер. На нем останавливались и авторы ряда исследова­ний, публиковавшихся в нашей психологической ли­тературе. Чрезвычайно важно поэтому выяснить его причины.

Под переносом обычно разумеют применение сложившегося у индивида и закрепленного в виде навыка способа действия в новых условиях, при ре­шении других аналогичных задач. Однако и закреп­ляющийся в виде навыка способ решения задачи должен быть сперва найден. Поэтому в конечном счете в плане мышления проблема "переноса" преобразует­ся в проблему применения прежде найденных решений (знаний) к новым задачам.

За фактами отсутствия переноса решения с од­ной задачи на другую, ей аналогичную, стоит недо­статочный анализ условий задачи соотносительно с ее требованиями и вытекающая отсюда недостаточ­ная обобщенность решения.

Условия, в которых дается задача, включают обычно в более или менее нерасчлененном виде соб­ственно условия задачи, т. е. те данные, которые уча­ствуют в решении, с которым это последнее необ­ходимо связано, и ряд привходящих обстоятельств (то или иное расположение чертежа, та или иная формулировка задачи и т. п.).

Для того чтобы решение задачи оказалось для учащегося (испытуемого) переносимым на другие случаи, отличающиеся от исходных лишь несуще­ственными, привходящими обстоятельствами (тем или иным расположением фигур и т. п.), необходи­мо (и достаточно), чтобы анализ через соотнесение

* Хрестоматия по общей психологии. Психология мышления /Под ред. Ю.Б.Гиппенрейтер, В.В.Петухова. М.: Изд-во Моск.ун­та, 1981. С. 281-288.

с требованиями задачи вычленил собственно усло­вия задачи из различных привходящих обстоятельств, в которых они непосредственно выступают сначала. Невозможность переноса решения в другую ситуа­цию (при изменении положения фигуры и т. п.) объясняется отсутствием такого анализа и отсюда вытекающей недостаточной обобщенностью реше­ния задачи. Мало того, чтобы реализовать даже обоб­щенное решение в новых обстоятельствах, нужно не просто его "перенести", а, сохраняя его по суще­ству, соответственно соотнести его с этими обстоя­тельствами, т. е. проанализировать и их (иногда через это соотнесение осуществляется и самое обобщение решения, выступающее в этом случае как результат синтетического акта).

В основе переноса лежит обобщение, а обобще­ние есть следствие анализа, вскрывающего суще­ственные связи. Анализа требуют как сама задача, условия, в которых она первоначально решается, так и те видоизмененные условия, на которые это ре­шение переносится.

С переносом решения одной и той же задачи в разные условия (обстоятельства) тесно связан пере­нос решения из одной задачи на другую, однород­ную с ней в том или ином отношении. Этот послед­ний случай был подвергнут у нас специальному ис­следованию.

Опыты К. А. Славской показали, что перенос совершается в том и только в том случае, когда обе задачи соотносятся и включаются испытуемыми в процессе единой аналитико-синтетической деятель­ности. Конкретно это выражается в том, что условия одной задачи анализируются через их соотнесение с требованиями другой. Для осуществления переноса решения требуется обобщение, связанное с абстрак­цией от несущественных моментов первой задачи и конкретизацией его применительно ко второй. Глав­ную роль при переносе играет анализ основной за­дачи, подлежащей решению. Течение процесса обоб­щения и осуществление переноса зависят главным образом от степени проанализированное™ той ос­новной задачи, на которую должен быть совершен перенос. Если вспомогательная задача предъявлялась на начальных этапах анализа основной, то она ре­шалась сперва самостоятельно, безотносительно ко второй; обобщение совершалось в результате развер­нутого соотнесения свойств и отношений обеих за­дач. Если вспомогательная задача предъявлялась, когда анализ основной задачи был уже значительно продвинут, то вспомогательная задача решалась сразу через соотнесение с требованиями основной, как звено этой последней. В этом случае обобщение со­вершается в ходе решения вспомогательной задачи. Поэтому нет нужды в специальном применении од­ной задачи к другой: перенос осуществляется с мес­та, сразу.

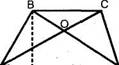
Эксперимент, в ходе которого это вскрылось, велся следующим образом: экспериментатор пред­лагал испытуемому решить задачу, рассуждая вслух: ход рассуждений испытуемого при решении задачи подробно протоколировался. Испытуемым - учащим­ся 7—9-х классов средних школ — давалась основная задача: доказать равновеликость треугольников АВО и OCD, заключенных между диагоналями трапеции (решение ее заключается в выделении треугольни-

A E DA D Рис. 1 Рис. 2

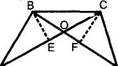
Рис. 3

ков ABD и ACD, которые равновелики, так как имеют общее основание AD и общую высоту трапе­ции, искомые треугольники являются частью дан­ных и поэтому равновелики) (рис. 1). Для исследова­ния переноса решения с одной задачи на другую испытуемым в ходе решения одной (основной) за­дачи давалась другая, вспомогательная. В эксперимен­тальную группу включались только те из обследо­ванных испытуемых (48 школьников и 12 студентов), которые решали основную задачу с помощью вспо­могательной и на которых поэтому можно было про­слеживать ход переноса. Во вспомогательной задаче нужно было доказать равенство диагоналей прямоу­гольника ABCD. Они равны, так как равны треу­гольники ABD и ACD, имеющие общее основание AD, равные стороны АВ и CD и равные прямые углы (рис. 2). Основная задача решается с помощью вспо­могательной посредством переноса на нее решения вспомогательной задачи. Общим звеном в решении обеих задач было использование общего основания AD треугольников ABD и ACD, которое в одном случае используется как общее основание равных, в другом - равновеликих треугольников. Таким обра­зом, чтобы решить основную задачу, т. е. найти рав­новеликие фигуры, связанные с искомыми и имею­щие равные (общие) высоты и общее основание, нужно выделить это звено решения вспомогатель­ной задачи как общее для обеих задач, т.е. произвес­ти обобщение.

Чтобы проследить зависимость обобщения от анализа основной задачи, вспомогательная задача предъявлялась испытуемым на разных этапах анали­за основной.

В качестве ранних этапов в специальном, узком смысле слова мы выделяли те, на которых испытуе­мые оперировали, анализировали и т. д. лишь с тем, что было непосредственно дано в условиях задачи; под поздними этапами анализа мы соответственно разумели те стадии решения задачи, на которых ис­пытуемые уже выделяли новые условия, выходящие за пределы того, что было непосредственно дано в исходных условиях задачи.

Конкретно различение более ранних и более позд­них этапов анализа основной задачи в наших экспе­риментах осуществлялось следующим образом.

Одной части испытуемых вспомогательная зада­ча давалась в тот момент, когда они анализировали непосредственно данные в задаче условия, т. е. на

ранних этапах анализа задачи. Эти испытуемые про­водили высоты треугольников АВО и OCD и анали­зировали их равновеликость, т.е. пытались доказать равенство их высот и оснований (рис. 3). Вначале, следовательно, они анализировали то, что непос­редственно дано в условии задачи — равновеликость треугольников АВО и OCD.

В ходе проб испытуемые убеждались в невозмож­ности доказать равновеликость АВО и OCD через равенство их высот и оснований. Они продолжали анализировать задачу дальше, выявляли новые, не данные им условия. Так, они выделяли другие фигу­ры, связанные с искомыми, чтобы первоначально доказать их равновеликость, рассматривали их вы­соты и основания (например, треугольников ABD и BCD с общей высотой трапеции и основаниями, которые являются верхним и нижним основаниями трапеции). Это выделение в ходе анализа задачи но­вых условий мы принимали за поздние этапы анали­за задачи. Второй группе испытуемых вспомогатель­ная задача предъявлялась на этих поздних этапах ана­лиза основной.

Чтобы "перенести" решение с одной задачи на другую, нужно найти обобщенное решение обеих задач. Предъявляя вспомогательную задачу на раз­ных этапах анализа основной задачи, мы прослежи­вали, как осуществляется обобщение в зависимости от степени проанализированное™ основной задачи, зависимость обобщения от анализа.

Испытуемые первой группы, которым вспомога­тельная задача предъявляется на ранних этапах ана­лиза основной, решают вспомогательную задачу как самостоятельную, не связанную с основной. После решения вспомогательной задачи испытуемые возвра­щались к решению основной задачи. При этом боль­шая часть испытуемых начала соотносить дальнейшее решение основной задачи со вспомогательной.

Таким образом, получается, что начальные эта­пы, или низшие уровни мышления, сами создают предпосылки, которые ведут к высшим. "Мотивом", побуждавшим к этому соотнесению, служило то, что испытуемые уже до осуществления сколько-нибудь развернутого и углубленного соотнесения задач усматривали, что между обеими задачами есть что-то общее, раскрывающееся затем в результате этого соотнесения, так как никаких указаний на связь обеих задач испытуемым не давалось; более того, чтобы не наводить испытуемых на эту мысль, эксперимента­тор предъявлял вспомогательную задачу с нарочито маскировочной установкой, говоря испытуемым, что вторая вспомогательная задача дается им для пере­дышки. Следовательно, оказывается, что сам ход ре­шения задачи создает внутренние условия для даль­нейшего движения мысли, причем эти условия вклю­чают в себя не только предпосылки логически-пред­метные, но и мотивы мышления, "двигатели" его. Со­отнесение (синтез) задач осуществлялось так, что, продолжая решение основной задачи, испытуемые анализировали в ней те же геометрические элемен­ты (углы, равные стороны, равные диагонали), ко­торые они использовали при решении вспомогатель­ной задачи.

Так, например, испытуемый Д. В. говорит: "Здесь же трапеция - совсем другое дело. Здесь диагонали не равны и боковые стороны тоже. Я не

знаю, чем мне здесь могут помочь диагонали..." (про­токол № 17).

Протоколы показывают, что, анализируя усло­вия основной задачи, испытуемые выделяют элемен­ты, использовавшиеся во вспомогательной задаче, для доказательства равенства треугольников. Все ис­пытуемые анализируют в условиях основной задачи общие, сходные со вспомогательной задачей усло­вия. Условия основной задачи анализируются через соотнесение с требованием вспомогательной.

Испытуемый Д. В. говорит: "Мне нужно доказать равновеликость треугольников". Испытуемый переходит к анализу новых условий, убеждаясь в невозможности использовать для реше­ния данные в условии задачи треугольники.

"Очевидно, что прямо и через равенство данных треугольников доказать нельзя, — говорит он, — мо­жет быть, можно через треугольники ABD и ACD?". Так испытуемый Д. В. переходит к выявлению новых условий основной задачи. Это создает предпосылки для привлечения новых условий из вспомогательной задачи (через соотнесение с требованием основной). Из всех наиденных в ходе предшествующего анализа геометрических элементов (равных сторон, диагона­лей и т. д.) привлекается к решению основной за­дачи только общее основание AD — для доказатель­ства равновеликости треугольников ABD и ACD. Испытуемый Д. В. говорит: "Равенство углов нам не нужно, равенство диагоналей тоже не нужно, а общее основание мы можем использовать". Таким образом, испытуемый выявляет то общее звено решения, которое является существенным и для основной задачи. Происходит обобщение — в гео­метрическом элементе, использовавшемся при ре­шении вспомогательной задачи (для доказательства равенства), выявляется новое свойство, существен­ное с точки зрения требования основной задачи (для доказательства равновеликости треугольников). Таким образом, оказывается, что ни одно из звеньев реше­ния вспомогательной задачи не привнесено извне в основную задачу; каждое звено решения основной задачи оказывается выявленным в результате анали­за самой основной задачи, ее условий, ими обус­ловленных отношений ее элементов, поэтому оно выделяется как общее, т. е. отвечающее требованию основной задачи, т. е. существенное для нее. Так про­исходит движение анализа от выявления общего как сходного к выделению общего, существенного для основной задачи.

Итак, при предъявлении вспомогательной задачи на ранних этапах анализа основной испытуемые пер­вой группы решают вспомогательную задачу как са­мостоятельную, не связанную с основной. Обобще­ние совершается постепенно в ходе дальнейшего ана­лиза основной задачи, осуществляющегося через со­отнесение сначала с требованием вспомогательной, затем основной задачи. Движение процесса соверша­ется от выявления сходного к выделению существен­ного через анализ и соотнесение обеих задач.

Вторая группа испытуемых, которая получила вспомогательную задачу на поздних этапах анализа основной задачи, решала вспомогательную задачу не как самостоятельную, а как непосредственное про­должение основной.

Так, например, решая вспомогательную задачу, где надо доказать равенство диагоналей, рассмотрев

равенство треугольников, испытуемая Л. Г. говорит; "Они рамы, т. е. у них общее основание, АВ и CD — общие высоты" (протокол № 16).

Таким образом, испытуемая абстрагировалась от всех моментов (равенство углов и треугольников), которые были несущественны для основной задачи, где речь шла не о равенстве, а о равновеликости. Вместе с тем те прямые, которые во вспомогатель­ной задаче являются сторонами, она обозначает как равные высоты и общее основание, т. е. сразу выде­ляет их в связи с основной задачей, связывает их и с доказательством равенства (как того требовала вспо­могательная задача), и с доказательством равнове­ликости (в соответствии с требованием основной задачи). Испытуемая Л.Г. анализирует условия вспо­могательной задачи не только через соотнесение с ее собственным требованием, но и одновременно с тре­бованием основной задачи.

В этом случае обобщение совершается уже в ходе решения вспомогательной задачи. Решение вспомо­гательной задачи служит как бы ответом на основ­ную задачу, включается как недостающее звено ана­лиза в решении последней. Обобщение совершается с "места" сразу, и нет необходимости в специальном действии применения одной задачи к другой. Это говорит о том, что именно обобщение, совершаю­щееся при решении вспомогательной задачи, состав­ляет истинную сущность того, что обозначается как перенос решения из задачи в задачу.

Таким образом, при предъявлении вспомогатель­ной задачи на поздних этапах анализа основной вспо­могательная задача решается испытуемыми второй группы уже не как самостоятельная, а в связи с основ­ной. Условия вспомогательной задачи анализируют­ся через соотнесение с требованием основной зада­чи, а не только через соотнесение с ее собственным требованием. В силу того, что основная задача про­анализирована испытуемыми до предъявления вспо­могательной, они сразу выделяют одно из звеньев решения вспомогательной задачи как существенное для основной задачи: обобщение совершается сразу в ходе решения вспомогательной задачи.

Таким образом, сравнивая результаты экспери­ментов, проведенных с двумя группами испытуемых (получившими вспомогательную задачу на ранних и на поздних этапах анализа основной), можно ска­зать следующее. От степени проанализированное™ основной задачи зависит то, как конкретно совер­шаются обобщение и перенос, к которому приводит обобщение: развернуто, постепенно, в результате анализа элементов и отношений обеих задач или уже в ходе решения вспомогательной задачи "с места", сразу. Следовательно, от анализа основной задачи зависит, когда и как совершается обобщение. Это говорит о зависимости обобщения от анализа. Ход анализа основной задачи определяет, как совершится обобщение задач.

Однако, как видно из рассмотренного экспери­ментального материала, обобщение подготовляется не в ходе анализа одной только основной задачи. Анализ того же экспериментального материала выя­вил также, что основным условием обобщения яв­ляется включение обеих задач в единую аналитико-синтетическую деятельность.

Только единая аналитико-синтетическая деятель­ность, включающая обе задачи, приводит к выделе­нию общих звеньев, т. е. к переносу.

Эта закономерность была не среднестатистичес­кой, а всеобщей закономерностью. Она выступила у всех без исключения 38 испытуемых, которым вспо­могательная задача предъявлялась после основной, так же как и у всех 10, которым она предъявлялась до основной задачи. Та же закономерность, полученная сначала на основной группе испытуемых (школьни­ков), проявилась и у 12 студентов, с которыми для сравнения проводились те же эксперименты.

<...> Исследование наше показало, что, как уже отмечалось, продуктивное соотнесение вспомога­тельной задачи с основной совершается только на поздних этапах анализа последней. Это положение имеет, с нашей точки зрения, принципиальное зна­чение, поскольку оно, по существу, означает, что использование "по