Препятствия при решении задач

До сих пор мы касались лишь общей структуры процесса решения задач — постоянной направленности на цель, иерархии и лежащих в ее основе мнемонических алгоритмов и программ действия. Однако некото­рые задачи — будь то капризный кроссворд или разрушительный про­фессиональный конфликт — кажутся абсолютно неразрешимыми. Могут ли наши знания о решении задач помочь подступиться к этой проблеме?

Мы уже упоминали один важный фактор: при решении задачи и новички, и мастера используют какие-то свои навыки и приемы всякий раз, когда берутся за ее выполнение. Некоторые из этих приемов вполне разумны и эффективны. Например, водитель такси, даже новичок, не тра­тит времени на размышление о том, не станет ли автокар самым лучшим транспортом до аэропорта, и даже неопытный повар понимает, что мари­нованные томаты не будут аппетитным украшением для утренних булочек. Но иногда эти базовые приемы вредны или, по крайней мере, непригодны в существующей ситуации. Будучи уверенным в успехе, индивид может стать жертвой своих, часто не замечаемых им самим, приемов, поскольку он введен в заблуждение сильной мыслительной установкой.

Этот вывод подтверждается широко известными экспериментами, которые демонстрируют, как люди могут зацикливаться на одном методе решения, будучи не в состоянии взглянуть на задачу под каким-то другим углом. Участникам одного эксперимента объясняли условие задачи: у них есть три сосуда: А, Б и В. Сосуд А вмещает ровно 21 л; сосуд Б — ровно

¹ Глейтман Г., Фридлунд А., Райсберг Д. Основы психологии. СПб.: Речь, 2001. С. 369-374.

Глейтман Г., Фридлунд А., Райсберг Д. [Препятствия при решении…] 543

127 л; сосуд В — ровно 3 л. Задача участников заключалась в том, чтобы достать из колодца ровно 100 л, ис­пользуя эти три сосуда.

Испытуемым потребовалось не­сколько минут, чтобы решить эту за­дачу. Решение состоит в том, чтобы наполнить сосуд Б полностью, затем перелить из Б в А столько воды, что­бы заполнить его. Теперь в сосуде Б осталось 106 л (127—21). Затем от­лить из Б столько воды, чтобы запол­нить В. В сосуде Б осталось 103 л (106—3). Наконец, вылить воду в ко­лодец из сосуда В и наполнить его вновь из Б, оставив там требуемое количество — 100 л (рис. 1).

Затем испытуемые выполнили еще несколько заданий подобного типа. Объемы сосудов в каждой зада­че были разными (табл. 1), но в каж­дом случае решение можно было по­лучить с помощью той же последова­тельности действий: наполнить сосуд Б, затем перелить воду в А; напол­нить В, перелив воду из Б; опорож­нить В и заполнить его вновь водой из Б. Другими словами, в каждом случае требуемый объем воды получался из следующего алгоритма: Б — А — 2В.

Когда участники решили пять таких задач, они получили две конт­рольные задачи. Первой была задача, где требовалось получить 20 л с по­мощью сосудов объемом 23, 49 и Зл. Испытуемые быстро решили задачу, используя тот же алгоритм: 49 — 23 — (3 х 2). Они уверенно оставили без внимания возможность простейшего способа решения этой задачи, кото­рый требовал всего лишь одного дей­ствия (рис. 2).

После этого испытуемых попро­сили получить 25 л воды, имея сосу-

Тема 18. Экспериментальные исследования мышления

Таблица 1 Задача с тремя сосудами

Требуемый объем воды, л	Объем пустого сосуда,	л
А	Б		В

ды объемом 28, 76 и 3 л. Единственным возможным решением здесь яв­ляется простое вычитание, то есть 28 - 3 — 25 (рис. 3). Но мыслительная установка оказалась настолько сильной, что многие вообще не смогли решить эту задачу. Они испробовали старый метод, но он не привел их к цели: 76 - 28 - (2 х 3) * 25, и они не смогли додуматься до нужной аль­тернативы! Установка сделала их настолько ригидными, что превратила в умственно отсталых¹.

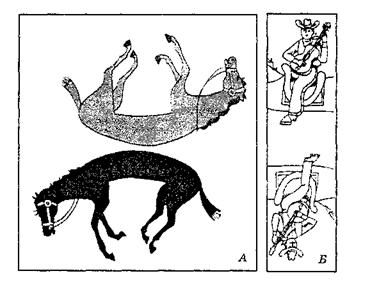
Рис. 4. Задача про всадников и лошадей. Задание: <...> разместить Б на А таким образом, чтобы всадники оказа­лись сидящими верхом на лошадях² (ответ см. на рис. 6)

¹ См.: Luchins A.S. Mechanization in problem-solving: The effect of Einstellung //
Psychological Monographs. 1942. 54. Wol. 248.

² См.: Scheerer M, Goldstein K, Boring E.G. A demonstration of insight: The horse-rider
puzzle // American Journal of Psychology. 1941. 54. P. 437-438.

Глейтман Г., Фридлунд А., Райсберг Д. [Препятствия при решении,,.] 545

Другие типы задач приводят к тому же результату. Во многих слу­чаях испытуемому не нужно навязывать обманчивую установку с помо­щью инструкций и предварительных упражнений, поскольку она вызы­вается перцептивной организацией самой задачи. Примерами таких ус­тановок, рожденных нашим восприятием, может служить <...> задача про всадников и лошадей (рис. 4).

Преодоление препятствий на пути к решению задач

Мы должны еще раз подчеркнуть, что мыслительная установка как таковая — вещь полезная, она позволяет решающему задачу сосредото­читься на конструктивных направлениях и избежать бессмысленных дей­ствий. Однако те же самые установки могут создать затруднения, застав­ляя нас задаться вопросом о том, как можно их преодолеть. Мы уже от­мечали важное значение знакомых программ и алгоритмов. Но что нам делать, если не удается выделить подзадачи или нам незнаком тот алго­ритм, который требуется для решения?

Обратное действие

Одним из полезных приемов при решении задач является обратное действие, когда поиск решения начинается с конца и идет в обратном направлении, двигаясь к исходной точке. Рассмотрим такую задачу.

Количество водяных лилий на поверхности озера удваивается каждый день. В первый день лета на озере росла только одна лилия. Потребовалось 60 дней, чтобы озеро полностью покрылось лилиями. В какой по счету день озеро было покрыто наполовину?

Задача может быть решена следующим образом. В первый день есть одна лилия; во второй — две лилии; в третий — четыре и т.д. При дос­таточном терпении этот метод приведет нас к заключению, что на 60-й день на озере было 580 млрд. лилий; половина из них — это 290 млрд., которые появились бы на 59-й день. Однако существует очень простой путь, который избавляет от этих громоздких вычислений: если озеро покрыто полностью на 60-й день, оно должно быть покрыто наполовину в предыдущий день, поскольку количество лилий удваивается каждый день; следовательно, правильный ответ — 59-й день¹ <...>.

¹ См.: Sternberg R.J., Davidson J.E. Insight in the gifted // Educational Psychologist. 1983. 18. P. 51-57.

Тема 18. Экспериментальные исследования мышления

Решение по аналогии

В качестве еще одного приема, помогающего при решении трудных задач, можно предложить решение по аналогии, поскольку многие зада­чи похожи друг на друга. Школьный психолог часто сталкивается с тем, что проблема, о которой ему рассказывают сегодня, напоминает ту, кото­рая была несколько месяцев назад, и первый опыт может помочь ему справиться со второй. Ученый, пытающийся дать объяснение новому явле­нию, часто находит ответ, анализируя прошлые явления, схожие с дан­ным. Аналогии сыграли важнейшую роль в истории науки; вспомним ученых, которые расширяли свои знания о газах, сравнивая молекулы с бильярдными шарами, или давали объяснение работе сердца, сравнивая его с насосом¹.

В одном из исследований участникам была предложена такая за­дача.

У больного — неоперабельная опухоль в брюшной полости. Существуют та­кие лучи, которые при достаточной интенсивности могут разрушить эту опу­холь. Однако при такой интенсивности лучи разрушат и здоровую ткань вок­руг опухоли (стенки желудка, брюшные мышцы и т.д.). Как избавить боль­ного от опухоли, не причиняя вреда здоровой ткани, через которую должны пройти эти лучи?²

Эта задача чрезвычайно сложна: в первой группе 90% участников не смогли ее решить. Вторая группа справилась намного лучше. До того как решать задачу с опухолью, они прочитали историю о генерале, ко­торый хотел захватить крепость. Для этого ему требовалась большая ар­мия солдат, но все дороги к крепости были заминированы. Маленькая группа солдат могла пройти по дороге, но более крупная группа обяза­тельно подорвалась бы на мине. Как же генералу провести к крепости всех солдат? Он разделил свою армию на маленькие группы и перепра­вил их по разным дорогам. По данному им сигналу все группы напра­вились к крепости, где объединились. После успешной атаки они захва­тили крепость.

По своей структуре история о крепости похожа на задачу с опухо­лью. В обоих случаях решение заключается в разделении «боевой силы» таким образом, чтобы она подходила из нескольких разных источников. Для того, чтобы уничтожить опухоль, сквозь здоровую ткань нужно про-

¹ См.: Gentner D., Jeziorskiy M. Historical shifts in the use of analogy in science //
B.Gholson, W.Shadish, R.Neimeyer, A.Houts. (Eds.). Psychology of science: Contributions
to metascience. Cambridge: Cambridge University Press, 1989.

² См.: Duncker K. On problem solving // Psychological Monographs. 1945. Wol. 270.
P. 1-113.

Глейтман Г., Фридлунд А., Райсберг Д. [Препятствия при решении...] 547

Рис. 5. Решение задачи с облучением опухоли

пустить несколько слабых лучей, каждый — разным путем. Лучи скон­центрируются на опухоли и окажут суммарное воздействие (рис. 5).

Несколько слабых лучей исходят из различных точек снаружи та­ким образом, чтобы соединиться на месте опухоли. В этом месте доза облучения будет сильной, так как в данной точке суммируется их общее действие. Но поскольку каждый луч сам по себе слаб, лучи не причиня­ют вреда здоровой ткани, окружающей опухоль¹

Без подсказок, инструкций или знания аналогичных случаев 90% участников первой группы не смогли решить задачу с опухолью. Одна­ко, когда им дали прочитать историю о крепости и сказали, что она им поможет, большинство (80%) решило задачу. Безусловно, аналогии чрез­вычайно полезны. Но недостаточно просто знать историю о крепости, испытуемые должны были понять и то, что эта история связана с дан­ной задачей. Удивительно, но многие не увидели здесь никакой анало­гии: участникам еще одной группы дали прочитать историю о крепости, но не намекнули на то, что эта история относится к их задаче. При та­ких условиях только 30% испытуемых решило задачу с опухолью.

¹ См. там же. Р. 1-113.

Тема 18. Экспериментальные исследования мышления

Рис. 6. Решение задачи про всадников и лошадей

Для того чтобы решить эту задачу, необходимо изменить перцеп­тивную установку. Часть А нужно повернуть на 90°, чтобы лошади ока­зались в вертикальной позиции. Теперь можно заметить, что голову од­ной (вертикальной) лошади можно совместить с задней частью другой. Последний шаг состоит в том, чтобы наложить Б на середину А¹.

¹ См.: Scheerer M., Goldstein К., Boring E.G. A demonstration of insight: The horse-rider puzzle // American Journal of Psychology. 1941. 54. P. 437-438.

А.Н. Леонтьев

ОПЫТ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ МЫШЛЕНИЯ¹

Среди психологических вопросов, относящихся к проблеме мышле­ния, одним из наиболее важных является вопрос о том специфическом звене мыслительной деятельности, который придает ей отчетливо выра­женный творческий характер.

Когда ученый или изобретатель, рабочий-рационализатор или уча­щийся стоят перед новой, впервые осваиваемой ими задачей, то обычно процесс решения такой задачи имеет как бы два этапа: первый этап — нахождение адекватного принципа, способа решения, который прямо не вытекает из условий задачи; второй этап — применение найденного уже принципа решения; вместе с тем это этап проверки и, часто, преобразо­вания данного принципа в соответствии с условиями конкретной решае­мой задачи.

Иногда этот второй этап требует большого времени и труда, но все же — это этап только дальнейшей разработки и конкретизации реше­ния, которое в своем общем виде, т.е. именно в принципе, уже найдено, уже известно.

Другое дело — первый этап, этап нахождения самого принципа или, как иногда говорят, идеи решения. Это и есть наиболее творческое, если можно так выразиться, звено мыслительной деятельности.

В психологической, и не только в психологической, литературе многократно описывались те черты, которые характеризуют мыслитель­ный процесс на этом его этапе. Главная из них, как известно, состоит в том, что после первоначально бесплодных попыток найти решение зада­чи внезапно возникает догадка, появляется новая идея решения. При этом очень часто подчеркивают случайность тех обстоятельств, в кото-

¹ Доклады на совещании по вопросам психологии 3-8 июля 1953 г. М.: Изд-во АПН РСФСР, 1954. С. 5-12.

Тема 18. Экспериментальные исследования мышления

рых происходит такое внезапное открытие новой идеи, нового принци­па решения.

Например, один из конструкторов шагающего экскаватора бросает случайный взгляд на человека, несущего чемодан, и ему приходит в го­лову совершенно новый принцип устройства, регулирующего «шагание» этой грандиозной машины.

Что же представляет собою это так называемое творческое звено мыслительной деятельности?

Его недостаточная изученность, естественно, создавала почву для всякого рода идеалистических психологических концепций, включая сюда и гештальтистскую концепцию Elnslcht 'a.

Вместе с тем, надо признать, что подлинно научное исследование этой проблемы представляет собой задачу серьезного теоретического и практического значения.

Один из циклов исследований, ведущихся в настоящее время на кафедре психологии Московского государственного университета, мы и посвятили экспериментальному изучению этой проблемы.

Здесь мы имеем возможность изложить только некоторые, далеко не полные результаты этой работы, которая проводилась под нашим ру­ководством Я.А.Пономаревым и Ю.Б.Гиппенрейтер.

Остановимся раньше на общей методике опытов.

Прежде всего нам нужно было выбрать подходящий тип задач.

Понятно, что мы не могли взять для эксперимента по-настоящему значимые задачи, т.е. поставить испытуемого в положение, скажем, изоб­ретателя или исследователя.

Мы остановились поэтому на гораздо более простых задачах — за­дачах «на догадку».

Такие задачи отличаются тем, что они требуют для своего решения только таких знаний и умений, которые заведомо имеются у испытуе­мых. Вместе с тем, как правило, их решение сразу не находится, т.е. условия этих задач сразу не актуализируют у испытуемых нужных свя­зей, вызывающих применение адекватного способа решения. Наконец, этот тип задач характеризуется тем, что если принцип решения данной задачи найден, то его применение уже не представляет никакого труда и, таким образом, этап нахождения принципа решения практически со­впадает со вторым-этапом — этапом реализации этого решения.

Примером задач такого типа может служить следующая простей­шая задача, которой пользовался в своих опытах Я.А.Пономарев.

Испытуемому дается лист бумаги, на котором нарисованы четыре точки, расположенные в виде квадрата; задача состоит в том, чтобы пе­речеркнуть их тремя прямыми, не отрывая руки от рисунка, и вернуть­ся к начальной точке (рис. 1).

Как показал опыт, взрослые люди, не знающие заранее данной за­дачи, быстро решить ее не могут, хотя нужные для этого элементарные

Леонтьев А.Н. Опыт экспериментального исследования мышления 551

геометрические знания у них, несомненно,
имеются. Так, если эту задачу несколько ви­
доизменить и, например, поставить ее в сле­
дующей форме: «Опишите вокруг квадрата
треугольник», то она, конечно, решается
очень легко. Дело, очевидно, заключается в
том, что изображение четырех точек первона­
чально вызывает прочно закрепленное дей­
ствие соединения точек линиями, как это в
подавляющем большинстве случаев дей-
ствительно и происходит в нашем опыте.

Принцип же решения данной задачи состоит

в другом, а именно в том, чтобы пересечь изображенные точки, выведя линии за пределы площади, ограниченной этими точками.

Иначе говоря, условия данной задачи первоначально ак­туализируют связи не адекватные, адекватные же связи не актуализи­руются и не вступают в новую связь — в связь с условиями именно дан­ной задачи, хотя в других условиях, например, в условиях инструкции, они актуализируются очень легко.

Таков был тип задач, применявшихся в опытах.

Собственно же эксперимент заключался в том, что, взяв одну из таких задач в качестве основной, экспериментатор подводил испытуемо­го тем или другим дополнительным приемом к ее решению.

Эти приемы заключались в том, что испытуемый выполнял по тре­бованию экспериментатора какое-нибудь упражнение или решал какие-нибудь другие задачи, которые объективно содержали в себе решение основной задачи и поэтому могли выполнить наводящую роль.

Таким образом, мы получили возможность проследить, при каких же условиях опыт испытуемого наводит его на правильное решение, что, собственно, и выражается в так называемой догадке.

По этой методике были проведены многочисленные серии опытов, но мы изложим только некоторые, наиболее простые. В одной из первых серий опытов, проведенных Я.А.Пономаревым, в качестве основной была взята описанная выше задача с четырьмя точками.

Вопрос был поставлен так: не будет ли решаться эта задача, т.е. не будут ли актуализироваться этой задачей адекватные связи, если они будут специально закреплены в соответствующем упражнении, даваемом испытуемому перед тем, как он начнет решать задачу.

В качестве наводящих упражнений давались следующие: напри­мер, испытуемый должен был многократно снимать расположенные на шахматной доске четыре пешки тремя ходами фигуры, которая может «брать» пешки и как ферзь, и как «дамка» при игре в шашки. При этом пешки были расположены так, что испытуемый проделывал движение,

552 Тема 18. Экспериментальные исследования мышления

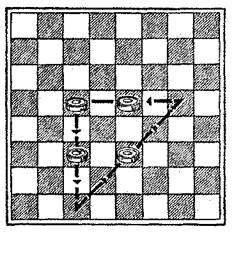путь которого совпадал с линиями перечеркивания точек в основной задаче (рис. 2).

Или второй пример наводящего упражнения: испытуемому предлага­лось многократно и различным обра­зом описывать вокруг квадрата треу­гольники.

Были введены и другие наводя­щие упражнения, описывать кото­рые мы здесь не будем.

Какое же действие оказали эти наводящие упражнения на решение предлагаемой вслед за ними задачи?

Рис. 2 многократное повторение отдель-

Полученные данные представ­ляются на первый взгляд неожи­данными, даже парадоксальными: ни ных упражнений, ни целые группы разных упражнений как преимуще­ственно второсигнального,так и первосигнального порядка не дали положительного эффекта: основная задача испытуемыми, предваритель­но проделавшими эти упражнения, не решалась.

Но может быть данные упражнения вообще не могут оказать наво­дящего действия? Это, однако, не так. Дело в том, что если эти же уп­ражнения дать после основной задачи, оставшейся нерешенной, то их наводящее действие отчетливо сказывается при вторичном предъявлении основной задачи и она чаще всего решается сразу же.

Итак: предварительное выполнение испытуемым задания, объек­тивно заключающего в себе способ решения основной задачи, не оказы­вает наводящего действия, и основная задача не решается.

Наоборот, выполнение такого же или аналогичного задания после безуспешных попыток решить основную задачу способно при определен­ных условиях приводить к ее решению «с места».

Этот факт многократно подтвержден в разных сериях опытов, на разных задачах, с помощью применения разных методик, включая чис­то лабораторную методику образования двигательных условных рефлек­сов, так что факт этот можно считать закономерным.

Анализ данного факта ставит два основных вопроса: во-первых, воп­рос о том, в силу чего задание, предшествующее основной задаче, не ока­зывает наводящего влияния; во-вторых, вопрос об условиях и закономер­ностях, характеризующих положительный эффект наводящего задания, когда оно дается после безуспешных попыток решить основную задачу.

Мы остановимся только на этом втором, в известном смысле более важном вопросе.

Вопрос этот был освещен в опытах Ю.Б.Гиппенрейтер.

Леонтьев А.Н. Опыт экспериментального исследования мышления 553

В этих опытах использовалась другая, тоже очень простая задача на догадку. Тре­бовалось сложить из 6 спичек четыре равно­сторонних треугольника. Раскладывая спич­ки на плоскости, это сделать невозможно. Чтобы решить эту задачу, надо было сло­жить объемную фигуру — тетраэдр, т.е. поднять спички над плоскостью (рис. 3).

В качестве наводящей применялась следующая задача: разместить на определен­ной площади несколько плоских коробок одинаковой толщины, но разных по контуру (это были обклеенные части обычной картон­ной коробки от папирос, разрезанной на куски неправильной формы).

Части коробки своей плоской стороной на заданной площади не размещались; чтобы сделать это, их нужно было поставить на ребро — вертикально (рис. 4).

После решения этой наводящей задачи испытуемый возвращался к прежде нерешенной им основной задаче, которая требовала применения того же самого принципа: отказа от построения на плоскости и построе­ния треугольника в трех измерениях.

Эксперимент состоял в систематическом варьировании одного из условий, в которых протекал опыт в целом, в то время как другие усло­вия оставались постоянными. При этом положительный эффект наводя­щей задачи сказывался не при всех условиях и не при всяком их соотно­шении, а закономерно зависел от определенных условий и от определен­ного соотношения этих условий.

Какие же это условия и соотношения, от которых зависит процесс наведения на решение, т.е. которые вызывают у испытуемого догадку, открытие принципа, позволяющего решить основную задачу сразу, «с места»?

Тема 18. Экспериментальные исследования мышления

Прежде всего была прослежена зависимость наводящего эффекта второй задачи от того, как испытуемые пытались найти решение первой, основной задачи.

Нужно сказать, что среди наших испытуемых выделилась группа, которая относилась к задаче с построением треугольников из спичек без всякого интереса. Стремление решить эту задачу у них очень скоро уга­сало, а некоторые из них прямо заявляли о том, что они не любят тако­го рода задач, что больше не хотят «ломать себе голову» и т.д.

В этом случае наводящая задача, хотя и решалась ими в наиболее эффективном ее варианте, но при вторичном возвращении к основной задаче последняя ими и на этот раз не решалась. Противоположный, т.е. положительный, эффект наводящей задачи наблюдался (при прочих рав­ных условиях) у всех испытуемых более активных, заинтересовавшихся основной задачей, у которых интерес к ней к моменту перехода к наво­дящей задаче не угасал.

Итак, первое простейшее положение, которое может быть сформу­лировано на основании этих опытов, заключается в следующем: для того, чтобы те или иные условия оказали воздействие, наводящее на искомое решение задачи, необходимо, чтобы эта задача вызывала у человека ин­терес, т.е. чтобы она создавала достаточно стойкую повышенную впечат­лительность или, пользуясь выражением Ухтомского, «подстерегатель-ность» к определенным раздражителям.

Ведь наведение и представляет собой не что иное, как один из случа­ев замыкания новой временной связи, а необходимым условием для этого является деятельное — и при этом избирательно деятельное состояние коры, т.е. именно наличие соответствующего доминантного очага возбуж­дения.

Свое дальнейшее развитие это первое положение получило в опы­тах с группой испытуемых, у которых желание искать решение основ­ной задачи не угасало.

Опыты велись так: одной части испытуемых давалась наводящая задача после безуспешных попыток решить основную задачу (со спичка­ми), когда у них возникало сомнение в возможности решить таким спо­собом эту задачу, но все же интерес к ней не пропадал; другой части испытуемых — в начале поисков решения, когда никакого сомнения в правильности избранного ими способа решения у них еще не возникало, им говорилось, что время на решение этой задачи истекло.

Как показал этот опыт, у первой подгруппы наводящая задача все­гда давала положительный эффект. Вторая же подгруппа испытуемых вела себя так: решив наводящую задачу и получив возможность снова решать основную задачу, испытуемые продолжали свои попытки, исхо­дящие из прежнего принципа, т.е. продолжали строить треугольники на плоскости, причем верного решения они так и не могли найти.

Итак: для того, чтобы произошло «наведение» на правильное реше­ние задачи, необходимо, чтобы возможности применения первого невер-

Леонтьев А.Н. Опыт экспериментального исследования мышления 555

ного принципа решения были исчерпаны, но чтобы вместе с тем это не вызвало бы полного угасания поисков решения задачи.

Последняя серия экспериментов, итоги которых мы кратко изло­жим, состояла в том, что в ней варьировались опыты с наводящей задачей.

В первом варианте экспериментатор давал испытуемому решать наводящую задачу в течение опыта несколько раз, начиная с первых же неудачных попыток испытуемого решить основную задачу, т.е. когда ее роль не могла еще сказаться, и до момента, который является наиболее благоприятствующим наведению на правильное решение. В этих услови­ях наводящая задача утрачивала для испытуемого свою новизну и пере­ставала вызывать живую ориентировочную реакцию раньше, чем насту­пал наиболее благоприятный момент для наведения на решение основной задачи. В результате такая «примелькавшаяся» испытуемому наводящая задача никакого действия оказать не могла.

Другой вариант состоял в том, что, при прочих равных условиях, наводящая задача резко упрощалась путем уменьшения площади, на которой нужно было уместить коробки, так что испытуемые сразу же ставили их на ребро. Это тоже снимало ее положительный эффект.

Таким образом, последнее положение, которое вытекает из опыта, заключается в следующем: наведение на правильное решение требует, чтобы наводящие обстоятельства вызывали у человека достаточно живую ориентировочную реакцию.

Наконец, необходимо отметить следующий характерный факт, вы­явившийся в опытах. Оказывается, обстоятельства и самый процесс на­ведения на решение задачи, т.е. замыкание соответствующих временных связей, не могут быть сколько-нибудь ясно отмечены самими испытуе­мыми. Напротив, этот момент обычно для них маскируется. Так, испы­туемые, например, отмечают, что при повторном предъявлении основной задачи ее решение наступает «как-то вдруг», а иногда дают явно непра­вильные указания вроде того, что задача решилась «потому, что есть такая фигура — тетраэдр».

Таким образом, изучавшееся нами звено мыслительной де­ятельности лежит вне возможности хоть сколько-нибудь правильно, даже хотя бы только описательно, представить его себе по данным са­монаблюдения, и его .изучение возможно лишь строго объективным ме­тодом. Вместе с тем, именно это звено является центральным во всякой интеллектуальной деятельности. Оно-то и представляет собой, как мы думаем, ту «ассоциацию ассоциаций», о которой упоминает И.П.Павлов, разбирая случаи «мышления в действии». Это — образование ас­социации между воздействующими условиями новой задачи и прежни­ми, уже имеющимися системами связей, которые были выработаны в других условиях; актуализируясь теперь в условиях новой задачи, они естественно сами развиваются дальше, видоизменяясь соответственно требованиям этих новых условий.

Тема 18. Экспериментальные исследования мышления

* * *

В заключение скажем несколько слов о перспективе дальнейшего исследования данного вопроса.

Мы думаем, что оно может быть продолжено, в частности, в направ­лении изучения творческого звена мыслительной деятельности в услови­ях усвоения, обучения.

Часто изображают этот процесс как якобы лишенный всякого твор­ческого момента, всякой живой догадки, открытия для себя новой идеи, что, по нашему мнению, глубоко неверно. Напротив, это очень важный момент усвоения.

С.Л. Рубинштейн

ОСНОВНАЯ ЗАДАЧА И МЕТОД

ПСИХОЛОГИЧЕСКОГО

ИССЛЕДОВАНИЯ МЫШЛЕНИЯ¹

Основная задача психологического исследования мышления заклю­чается в том, чтобы, не ограничиваясь фиксацией внешних результатов мыслительной деятельности, вскрыть самый процесс мышления во внут­ренних закономерностях его протекания.

Это — генеральная линия. Она реализуется в отношении ряда про­блем, где исследование умственной деятельности сводилось к описанию ее внешнего протекания, к констатации фактов, в которых она выражается, без раскрытия внутреннего закономерного процесса, приводящего к этим фактам. Показательным примером может служить проблема «переноса».

В педагогической практике учитель часто встречается с тем, что ученик, решивший задачу или как будто усвоивший теорему примени­тельно к данным условиям, оказывается не в состоянии «перенести» это решение в другие условия, решить ту же задачу, как только задача предъявляется ему в видоизмененных условиях. Это часто встречающий­ся и практически фундаментально важный факт. С констатации подоб­ных фактов начинает, как известно, свое исследование о «продуктивном мышлении» Вертгеймер. На нем останавливались и авторы ряда иссле­дований, публиковавшихся в нашей психологической литературе. Чрез­вычайно важно поэтому выяснить его причины.

Под переносом обычно разумеют применение сложившегося у ин­дивида и закрепленного в виде навыка способа действия в новых усло­виях, при решении других аналогичных задач. Однако и закрепляющий­ся в виде навыка способ решения задачи должен быть сперва найден. Поэтому в конечном счете в плане мышления проблема «переноса» пре-

¹ Хрестоматия по общей психологии. Психология мышления / Под ред. Ю.Б.Гиппен-рейтер, В.В.Петухова. М.: Изд-во Моск. ун-та, 1981. С. 281-288.

Тема 18. Экспериментальные исследования мышления

образуется в проблему применения прежде найденных решений (знаний) к новым задачам.

За фактами отсутствия переноса решения с одной задачи на другую, ей аналогичную, стоит недостаточный анализ условий задачи соотноси­тельно с ее требованиями и вытекающая отсюда недостаточная обобщен­ность решения.

Условия, в которых дается задача, включают обычно в более или менее нерасчлененном виде собственно условия задачи, т.е. те данные, которые участвуют в решении, с которым это последнее необходимо свя­зано, и ряд привходящих обстоятельств (то или иное расположение чер­тежа, та или иная формулировка задачи и т.п.).

Для того чтобы решение задачи оказалось для учащегося (испыту­емого) переносимым на другие случаи, отличающиеся от исходных лишь несущественными, привходящими обстоятельствами (тем или иным рас­положением фигур и т.п.), необходимо (и достаточно), чтобы анализ че­рез соотнесение с требованиями задачи вычленил собственно условия задачи из различных привходящих обстоятельств, в которых они непос­редственно выступают сначала. Невозможность переноса решения в дру­гую ситуацию (при изменении положения фигуры и т.п.) объясняется отсутствием такого анализа и отсюда вытекающей недостаточной обоб­щенностью решения задачи. Мало того, чтобы реализовать даже обобщен­ное решение в новых обстоятельствах, нужно не просто его «перенести», а, сохраняя его по существу, соответственно соотнести его с этими обсто­ятельствами, т.е. проанализировать и их (иногда через это соотнесение осуществляется и самое обобщение решения, выступающее в этом случае как результат синтетического акта).

В основе переноса лежит обобщение, а обобщение есть следствие анализа, вскрывающего существенные связи. Анализа требуют как сама задача, условия, в которых она первоначально решается, так и те видо­измененные условия, на которые это решение переносится.

С переносом решения одной и той же задачи в разные условия (об­стоятельства) тесно связан перенос решения из одной задачи на другую, однородную с ней в том или ином отношении. Этот последний случай был подвергнут у нас специальному исследованию.

Опыты К.А.Славской показали, что перенос совершается в том и только в том случае, когда обе задачи соотносятся и включаются испытуе­мыми в процессе единой аналитико-синтетической деятельности. Конкрет­но это выражается в том, что условия одной задачи анализируются через их соотнесение с требованиями другой. Для осуществления переноса реше­ния требуется обобщение, связанное с абстракцией от несущественных моментов первой задачи и конкретизацией его применительно ко второй. Главную роль при переносе играет анализ основной задачи, подлежащей решению. Течение процесса обобщения и осуществление переноса зависят главным образом от степени проанализированности той основной задачи,

Рубинштейн С.Л. Основная задача и метод...

на которую должен быть совершен перенос. Если вспомогательная задача предъявлялась на начальных этапах анализа основной, то она решалась сперва самостоятельно, безотносительно ко второй; обобщение совершалось в результате развернутого соотнесения свойств и отношений обеих задач. Если вспомогательная задача предъявлялась, когда анализ основной зада­чи был уже значительно продвинут, то вспомогательная задача решалась сразу через соотнесение с требованиями основной, как звено этой после­дней. В этом случае обобщение совершается в ходе решения вспомогатель­ной задачи. Поэтому нет нужды в специальном применении одной задачи к другой: перенос осуществляется с места, сразу.

Эксперимент, в ходе которого это вскрылось, велся следующим образом: экспериментатор предлагал испытуемому решить задачу, рассуждая вслух: ход рассуждений испытуемого при решении задачи подробно протоколировал­ся. Испытуемым — учащимся 7-9-х классов средних школ — давалась основ­ная задача: доказать равновеликость треугольников АВО и OCD, заключенных между диагоналями трапеции (решение ее заключается в выделении треуголь­ников ABD и ACD, которые равновелики, так как имеют общее основание AD и общую высоту трапеции; искомые треугольники являются частью данных и поэтому равновелики) (рис. 1). Для исследования переноса решения с одной задачи на другую испытуемым в ходе решения одной (основной) задачи дава­лась другая, вспомогательная. В экспериментальную группу включались толь­ко те из обследованных испытуемых (48 школьников и 12 студентов), которые решали основную задачу с помощью вспомогательной и на которых поэтому можно было прослеживать ход переноса. Во вспомогательной задаче нужно было доказать равенство диагоналей прямоугольника ABCD. Они равны, так как равны треугольники ABD и ACD, имеющие общее основание AD, равные стороны АВ и CD и равные прямые углы (рис. 2). Основная задача решается с помощью вспомогательной посредством переноса на нее решения вспомога­тельной задачи. Общим звеном в решении обеих задач было использование общего основания AD треугольников ABD и ACD, которое в одном случае ис­пользуется как общее основание равных, в другом — равновеликих треуголь­ников. Таким образом, чтобы решить основную задачу, т.е. найти равновели­кие фигуры, связанные с искомыми и имеющие равные (общие) высоты и об­щее основание, нужно выделить это звено решения вспомо<