Семантические правила для пропозициональных связок языка ЛВ
Семантические правила (вообще) – это правила, которые приписывают смысл и значение выражениям языка. Семантические правила языка ЛВ включают правила, которые приписывают точный смысл и значение пропозициональным связкам. Они также задаются на уровне метаязыка ЛВ и приписывают пропозициональным связкам функции истинности, т.е. истинно-истинностные пропозициональные функции. С практической точки зрения эти функции удобно представить в виде таблиц истинности, которые наглядно показывают, что истинностное значение сложного высказывания есть функция от истинностных значений высказываний, из которых оносостоит. Таким образом, каждая таблица истинности, приписывающая истинностное значение сложному высказыванию, образованному посредством определенной пропо-зициональной связки, репрезентирует в практической части ЛВ отдельное семантическое правило, которое превращает пропозициональную связку в логический союз. По числу пропозициональных связок мы таблично задаем шесть семантических правил.
1) Семантическое правило для конъюнкции.
Конъюнкция – «  »; читается «… и …»
»; читается «… и …»
С помощью конъюнкции образуются сложные конъюнктивные высказывания. Например: пусть А есть высказывание «8 делится на 2», а В есть высказывание «8 делится на 4». Тогда из них с помощью логического союза «и» можно образовать сложное конъюнктивное высказывание вида «А и В»: «8 делится на 2, и 8 делится на 4». Табличное правило для «  ».
».
| А | В | А  В В |
| И И Л Л | И Л И Л | И Л Л Л |
Из данного семантического правила следует, что конъюнктивное высказывание является истинным тогда и только тогда, когда все высказывания, из которых оно состоит, являются истинными (см. строку 1 таблицы), и ложным в противных случаях (см. строки 2, 3, 4).
Следует иметь в виду, что в естественном языке смысл логического союза «конъюнкция» передает не только грамматический союз «и», но и союзы «да», «а», «но», «а также» и другие. Например.
(1) Зимой солнце светит, да слабо греет.
(2) Я его ждал, но он не пришел.
(3) Иванов – футболист, а Петров – шахматист.
Это обстоятельство при формализации рассуждений средствами ЛВ требует от пользователя языка повышенного внимания в процессе логического моделирования содержательных рассуждений.
2) Семантическое правило для неисключающей дизъюнкции (Н- дизъюнкции).
Н-дизъюнкция – «  »; читается «… или…», где «или» имеет смысл: или первое, или второе, или оба вместе. Посредством Н-дизъюнкции образуются сложные Н-дизъюнктивные высказывания. Например. А – «Иванов – футболист», В – «Иванов – шахматист». Через «или» образуем Н-дизъюнктивное высказывание: «Иванов – футболист, или Иванов – шахматист». Очевидно, что в данном случае не исключается возможность одновременной истинности высказываний А, В, так как один и тот же человек Иванов может быть одновременно ифутболистом и шахматистом. Табличное семантическое правило для «
»; читается «… или…», где «или» имеет смысл: или первое, или второе, или оба вместе. Посредством Н-дизъюнкции образуются сложные Н-дизъюнктивные высказывания. Например. А – «Иванов – футболист», В – «Иванов – шахматист». Через «или» образуем Н-дизъюнктивное высказывание: «Иванов – футболист, или Иванов – шахматист». Очевидно, что в данном случае не исключается возможность одновременной истинности высказываний А, В, так как один и тот же человек Иванов может быть одновременно ифутболистом и шахматистом. Табличное семантическое правило для «  ».
».
| А | В | А  В В |
| И И Л Л | И Л И Л | И И И Л |
Из данного семантического правила следует, что Н-дизъюнктивное высказывание является ложным тогда и только тогда, когда все высказывания, из которых оно состоит, являются ложными (см. строку 4), и истинным в противных случаях (см. строки 1, 2, 3).
3. Семантическое правило для исключающей дизъюнкции (И-дизъюнкции). И-дизъюнкция – «  »; читается «…либо…», где либо понимается как «или первое, или второе, но не оба вместе». Пример сложного И-дизъюнктивного высказывания: «Это предложение – сложное, либо это предложение – простое». Очевидно, что простые высказывания, из которых состоит данное И-дизъюнктивное высказывание, не могут быть вместе истинными, т.е. в нем исключается случай одновременной истинности этих высказываний. Поэтому «
»; читается «…либо…», где либо понимается как «или первое, или второе, но не оба вместе». Пример сложного И-дизъюнктивного высказывания: «Это предложение – сложное, либо это предложение – простое». Очевидно, что простые высказывания, из которых состоит данное И-дизъюнктивное высказывание, не могут быть вместе истинными, т.е. в нем исключается случай одновременной истинности этих высказываний. Поэтому «  » называется «исключающей дизъюнкцией». Табличное семантическое правило для «
» называется «исключающей дизъюнкцией». Табличное семантическое правило для «  ».
».
| А | В | А  В В |
| И И Л Л | И Л И Л | Л И И Л |
Из данного семантического правила следует, что И-дизъюнктивное высказывание является истинным, когда высказывания, из которых оно состоит, принимают неодинаковые истинностные значения (см. строки 2, 3), и ложным в противных случаях (см. строки 1, 4).
Важно иметь в виду, что в естественном языке логический союз «  » также может передаваться грамматическим союзом «или». Например, высказывание: «Сегодня четверг или сегодня пятница» имеет логическую форму p
» также может передаваться грамматическим союзом «или». Например, высказывание: «Сегодня четверг или сегодня пятница» имеет логическую форму p  q, а не p
q, а не p  q. Данный пример наглядно показывает, что естественный язык строго не следует за логической формой высказываний, что во избежание ошибок всегда нужно помнить при формализации рассуждений.
q. Данный пример наглядно показывает, что естественный язык строго не следует за логической формой высказываний, что во избежание ошибок всегда нужно помнить при формализации рассуждений.
4. Семантическое правило для импликации. Импликация – « 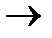 »; читается «Если… то…» Пример сложного импликативного высказывания, т.е. высказывания, образованного с помощьюлогического союза «
»; читается «Если… то…» Пример сложного импликативного высказывания, т.е. высказывания, образованного с помощьюлогического союза « 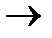 »(импликация): «Если идет дождь, то на улице сыро». Табличное семантическое правило для импликации, т. е. для «
»(импликация): «Если идет дождь, то на улице сыро». Табличное семантическое правило для импликации, т. е. для « 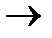 ».
».
| А | В | А 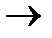 В В |
| И И Л Л | И Л И Л | И Л И И |
В выражении вида А 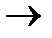 В принято различать антецедент (предшествующий член) импликации – А и консеквент (последующий член) импликации – В. Из данного семантического правила следует, что импликативное высказывание является ложным тогда и только тогда, когда его антецедент истинен, а консеквент ложен (см. строку 2). В противных случаях (см. строки 1, 3, 4) импликативное высказывание является истинным. Данное распределение истинностных значений в выходном столбце таблицы становится легко понятным, если учесть, что импликация «
В принято различать антецедент (предшествующий член) импликации – А и консеквент (последующий член) импликации – В. Из данного семантического правила следует, что импликативное высказывание является ложным тогда и только тогда, когда его антецедент истинен, а консеквент ложен (см. строку 2). В противных случаях (см. строки 1, 3, 4) импликативное высказывание является истинным. Данное распределение истинностных значений в выходном столбце таблицы становится легко понятным, если учесть, что импликация « 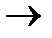 » есть формальный аналог дедуктивной выводимости (следования). Тогда в строке 1 мы утверждаем следующее интуитивно приемлемое логическое содержание: когда из истинного высказывания А мы выводим истинное высказывание В, то импликативное высказывание «Если А, то В» должно быть истинным;
» есть формальный аналог дедуктивной выводимости (следования). Тогда в строке 1 мы утверждаем следующее интуитивно приемлемое логическое содержание: когда из истинного высказывания А мы выводим истинное высказывание В, то импликативное высказывание «Если А, то В» должно быть истинным;
в строке 2: когда из истинного высказывания А мы выводим ложное высказывание В, то импликативное высказывание «Если А, то В» должно быть ложным;
строку 3 и 4 можно интерпретировать как из лжи выводимо все что угодно, поэтому импликативные высказывания «Если А, то В» в этих строках должны оцениваться как истинные.
В практике формализации рассуждений следует учитывать, что иногда грамматический оборот «если… то…» в естественном языке выражает конъюнкцию, а не импликацию. Например: «Если Иванов – физик, то Петров – историк». Смысл этого утверждения, если очистить его от эмоционального фона, равнозначен тому, что Иванов есть физик и Петров есть историк.
5. Семантическое правило для эквиваленции
Эквиваленция – «  »; читается «тогда и только тогда, когда…» («…если и только если…»). Примеры сложных высказываний эквивалентности, т. е. высказываний, образованных с помощью логического союза «
»; читается «тогда и только тогда, когда…» («…если и только если…»). Примеры сложных высказываний эквивалентности, т. е. высказываний, образованных с помощью логического союза «  » (эквиваленция), с двумя равнозначными его прочтениями.
» (эквиваленция), с двумя равнозначными его прочтениями.
(1) Тогда и только тогда треугольник равносторонен, когда он равноуголен.
(2) Треугольник равносторонен, если и только если он равноуголен.
Табличное семантическое правило для « 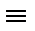 ».
».
| А | В | А  В В |
| И И Л Л | И Л И Л | И Л Л И |
Из данного семантического правила следует, что высказывание эквивалентности является истинным тогда и только тогда, когда высказывания, из которых оно состоит, принимает одинаковые истинностные значения (см. строки 1, 4), и ложным в противных случаях (см. строки 2, 3).
Приписывание указанных истинностных значений высказыванию эквивалентности становится вполне понятным, если учесть, что слово «эквивалентность» синонимично слову «равнозначность», что означает равные (одинаковые) истинностные значения для высказываний А, В.
6. Семантическое правило для отрицания.Отрицание – «  »; читается «неверно, что…» («не…»). С помощью отрицания образуются сложные отрицательные высказывания. Например, из ложного простого утвердительного высказывания «Варшава есть столица Франции» с помощью оборота «неверно, что…» образуется истинное сложное высказывание «Неверно, что Варшава есть столица Франции».
»; читается «неверно, что…» («не…»). С помощью отрицания образуются сложные отрицательные высказывания. Например, из ложного простого утвердительного высказывания «Варшава есть столица Франции» с помощью оборота «неверно, что…» образуется истинное сложное высказывание «Неверно, что Варшава есть столица Франции».
Семантическое правило для «  » (отрицания).
» (отрицания).
| А |  А А |
| И Л | Л И |
Более простая таблица для «  » объясняется тем, что «
» объясняется тем, что «  » является унарной пропозициональной связкой и применяется ровно к одному высказыванию – в отличие от «
» является унарной пропозициональной связкой и применяется ровно к одному высказыванию – в отличие от «  », «
», «  », «
», «  », «
», «  », «
», «  », которые являются бинарными пропозициональными связками и, следовательно, по меньшей мере применяются к двум высказываниям. Из данного семантического правила следует, что сложное отрицательное высказывание является истинным тогда и только тогда, когда отрицаемое высказывание является ложным и, наоборот, является ложным, когда отрицаемое высказывание является истинным.
», которые являются бинарными пропозициональными связками и, следовательно, по меньшей мере применяются к двум высказываниям. Из данного семантического правила следует, что сложное отрицательное высказывание является истинным тогда и только тогда, когда отрицаемое высказывание является ложным и, наоборот, является ложным, когда отрицаемое высказывание является истинным.
Виды формул. Законы ЛВ
Для выделения и описания законов ЛВ представим типологию формул ЛВ. В этой типологии мы выделим 5 типов формул и представим их в виде следующей диаграммы[32].
необщезначимые
I Тождественно-истинные (общезначимые) формулы Пример: p   p p |
II Нейтральные формулы Пример: p  q q |
III Невыполнимые (тождественно-ложные) формулы ЛВ Пример:  (p (p   p) p) |
(ПДФ13– 1)
выполнимые
Тождественно-истинные (общезначимые) формулы – это формулы, которые для всех (из числа возможных) наборов истинностных значений входящих в них пропозициональных переменных принимают только значение «и» (истина).
Нейтральные формулы – это формулы, которые для некоторых (из числа возможных) наборов истинностных значений входящих в них пропозициональных переменных принимают значение «и», а для некоторых других – принимают значение «л» (ложь).
Невыполнимые (тождественно-ложные) формулы – это формулы, которые для всех (из числа возможных) наборов истинностных значений входящих в них пропозициональных переменных принимают только значение «л».
Диаграмма показывает, что объединение тождественно-истинных и нейтральных формул образует класс выполнимых формул. Это такие формулы, которые принимают хотя бы одно значение «и». Соответственно объединение класса невыполнимых (тождественно-ложных) и нейтральных формул образует класс необщезначимых формул. Это такие формулы, которые принимают хотя бы одно значение «л».
Между тождественно-истинными и тождественно-ложными формулами существует следующая логическая связь: отрицание тождественно-истинной формулы дает тождественно-ложную формулу и, наоборот, отрицание тождественно-ложной формулы дает тождественно-истинную формулу.
Так же понятно, что отрицание нейтральной формулы даст только нейтральную формулу.
Мы знаем, что любые законы, в том числе и законы логики, представляются в языке общими и необходимо истинными высказываниями, т. е. номологическими высказываниями. Из вышеприведенных определений различных видов формул видно, что только тождественно-истинные (общезначимые) формулы выполняют условие номологического высказывания. Следовательно, законы ЛВ представляются классом тождественно-истинных формул.
