Синтаксические правила языка ЛВ
Под синтаксическими правилами любого языка в лингвистической семиотике понимают правила образования сложных выражений языка из простых. Эти правила фиксируют допустимые в данном языке способы сочленения языковых знаков. В аналитической философии XX столетия сформировался следующий образ точного языка: если выражение языка построено в соответствии с его синтаксическими правилами, то оно обладает смыслом; в противном случае оно бессмысленно, т.е. является языковой фикцией и должно быть устранено из языка.
Следует отметить, что естественные языки не удовлетворяют идеалу точного языка. Например, высказывание «В столовой было пусто» с синтаксической точки зрения неправильно построено, так как в нем ради облегчения коммуникации людей опущено существительное «комната», но это обстоятельство компенсировано тем, что в нем прилагательное «столовая» субстантивировано, т. е. стало выполнятьфункцию существительного. Темне менее это высказывание осмысленно и понимается одинаково всеми участниками процесса коммуникации.
В данном случае синтаксическая неточность языкового выражения не опасна, так как в данном высказывании субстантивированное прилагательное «столовая» есть простое общее имя, экстенсионал которого (множество предметов, подпадающих под это имя) есть множество эмпирических объектов, точные представления о которых имеются в опыте всех участников коммуникации.
Однако по-другому обстоит дело, когда язык употребляется в качестве средства познания объектов, не фиксируемых органами чувств человека, что имеет место в математике, теоретической физике, философии и в других науках, предметная область которых представлена сверхчувственными объектами. Здесь точность языка является одним из условий точности научной теории.
Это условие полностью распространяется и на ЛВ, одной из задач которой является точная запись в объектном языке логических форм, употребляемых в рассуждении высказываний.
Поэтому сформулируем точные синтаксические правила объектного языка ЛВ.
В ЛВ синтаксические правила объектного языка задаются в метаязыке ЛВ посредством индуктивного определения термина «формула».
Термин «формула» употребляется при этом в следующих трёх смыслах:
1) формула как логическая форма высказывания;
2) формула как правильно построенное выражение объектного языка ЛВ;
3) формула как линейно упорядоченная последовательность символов алфавита ОЯЛВ.
Под индуктивными определениями в математике и современной логике понимают неявные определения, позволяющие из некоторых исходных объектов теории с помощью некоторых операций строить все возможные в теории типы объектов. Примером применения индуктивного определения в математике является индуктивное определение выражения «натуральное число». Оно состоит из трёх пунктов:
1) 0 есть натуральное число;
2) Если n есть натуральное число, то n+1 также натуральное число;
3) Ничто иное не есть натуральное число.
По аналогии в ЛВ имеем следующее индуктивное определение выражения «формула ОЯЛВ», каждый пункт которого рассматривается как синтаксическое правило построения выражений ОЯЛВ.
1) Пропозициональная переменная есть формула ОЯЛВ.
Это правило утверждает, что любая пропозициональная переменная, т. е. p, q, r, s, является правильно построенным выражениемобъектного языка, так как она есть логическая форма простого высказывания.
2) Если A и B – формулы ОЯЛВ, то (A  B), (A
B), (A  B), (A
B), (A  B), (A
B), (A 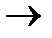 B) (A
B) (A  B), также являются формулами ОЯЛВ. Это правило задаёт все виды сложных правильно построенных выражений ОЯЛВ, так как они есть обобщённые логические формы сложных высказываний.
B), также являются формулами ОЯЛВ. Это правило задаёт все виды сложных правильно построенных выражений ОЯЛВ, так как они есть обобщённые логические формы сложных высказываний.
3) Если А есть формула ОЯЛВ и В есть формула ОЯЛВ, то (  A) и (
A) и (  B) также есть формулы ОЯЛВ. Это правило описывает логические формы сложных отрицательных высказываний.
B) также есть формулы ОЯЛВ. Это правило описывает логические формы сложных отрицательных высказываний.
4) Ничто иное не есть формула ОЯЛВ.
В этом определении пункты 1) – 3) представляют прямые синтаксические правила ОЯЛВ, а пункт 4) репрезентирует косвенное синтаксическое правило ОЯЛВ.
Сформулированные синтаксические правила являются эффективными в том смысле, что они позволяют для любого выражения ОЯЛВ, составленного из знаков его алфавита, в конечное число шагов дать однозначный ответ на вопрос: является ли оно формулой (правильно построенным выражением ОЯЛВ) либо таковой не является? Так, например, опираясь на синтаксические правила 1) – 3), мы можем в конечное число шагов последовательно приписать каждому структурному образованию выражения  (p
(p  q)
q)  (
(  p
p 
 q) значение Ф (формула) и в конечном счете – всему выражению, что демонстрирует следующая таблица:
q) значение Ф (формула) и в конечном счете – всему выражению, что демонстрирует следующая таблица:
 (p
(p  q)
q)  (
(  p
p 
 q)
q)
Ф Ф Ф Ф
Ф Ф Ф
Ф Ф
Ф
Нетрудно понять, что мы построили точный объектный язык ОЯЛВ, так как формула  (p
(p  q)
q)  (
(  p
p 
 q) легко наполняется следующим стилистически корректным конкретным содержанием (смыслом): тогда и только тогда неверно, что этот автомобиль купил Петров или этот автомобиль купил Иванов, когда его не купил Петров и его не купил Иванов. Равным образом можно таблично показать, что выражение → (p, q)
q) легко наполняется следующим стилистически корректным конкретным содержанием (смыслом): тогда и только тогда неверно, что этот автомобиль купил Петров или этот автомобиль купил Иванов, когда его не купил Петров и его не купил Иванов. Равным образом можно таблично показать, что выражение → (p, q)  (p
(p  q) не является формулой, т.е. не является правильно построенным выражением ОЯЛВ.
q) не является формулой, т.е. не является правильно построенным выражением ОЯЛВ.
Описанные синтаксические правила распространяются и на формульные схемы метаязыка ЛВ.
