Определение (дефиниция) как логическая операция и способ представления понятий в языке

6.1. Общая характеристика определения (дефиниции)

В повседневной жизни люди по мере овладения языком на интуитивном уровне стихийно приписывают смысл и значение языковым выражениям в зависимости от тех или иных условий жизни, в которых они оказались с детства. В силу этого в разговорных ситуациях часто возникает недопонимание между людьми, что может существенно осложнять их жизнедеятельность.

Особенно актуализируется проблема приписывания смысла и значения языковым выражениям в научном познании, где приписывание точного смысла и значения терминам (языковым выражениям) теории в значительной степени обусловливает научность самой теории. И ещё больше эта проблема актуализируется в гуманитарных и общественных науках. В этих науках теории и концепции формулируются средствами естественных языков, которые, в отличие от точных искусственных языков математики и современной логики, без предварительных уточнений смысла языковых выражений оказываются неадекватными средствами познания в силу широко распространенного в них явления омонимии.

Поэтому потребности практической и исследовательской деятельности людей обусловили появление в логике специальной процедуры, уточняющей смыслы выражений языка. Эта процедура получила название определения (дефиниции).

Русское слово «определение» является производным от слов «предел», «граница». Равным образом обстоит дело и с его эквивалентом «дефиниция», восходящим к латинскому слову «definitio», что также означает определение (см. Словарь лат. языка Дворецкого).

Таким образом, этимология этих слов подсказывает, что под определением (дефиницией) в логике следует понимать логическую операцию, которая раскрывает смысл выражений языка и тем самым косвенно указывает на их значения.

При этом в общей практической логике речь идёт прежде всего об определениях простых общих имён, ибо их определение наиболее актуально для познания вообще и для познания в гуманитарных и общественных науках в частности. Ведь целью любого познания является нахождение прежде всего общего в единичных явлениях (ситуациях). Понятно также, что нет необходимости определять описательные общие и описательные единичные имена, так как описательные имена, как мы отмечали выше, обладают исходным самостоятельным смыслом. Для общей практической логики также неактуально определять простые единичные имена и повествовательные предложения.

6.2. Виды определений

Все определения в логике делятся на явные и неявные. Явные определения – это определения, имеющие вид равенства и использующиеся в науках в качестве правил взаимозаменяемости терминов в предложениях языка. Соответственно неявные определения – это определения, которые не имеют вида равенства и которые не используются в науках в качестве правил взаимозаменяемости терминов.

Неявные определения широко используются в математических и математизированных науках, в том числе и в современной логике.

К их числу относятся индуктивные, рекурсивные, контекстуальные определения и определения через аксиомы. Ниже мы рассмотрим в рамках общей практической логики лишь один вид этих определений, а именно: индуктивное определение формулы логики высказываний (ЛВ), где сама ЛВ как раздел общей практической логики строится лишь на семантическом уровне, т.е. с использованием только таблиц истинности, определяющих смысл и значение логических связок, используемых для образования сложных суждений из простых.

Из явных определений мы рассмотрим лишь явные определения простых общих имен как наиболее употребляемый вид определений, используемый людьми в речевой практике и в гуманитарно-общественных науках.

6.3. Структура явных определений простых общих имен и их функции

В структуре явных определений выделяют следующие элементы:

1) Определяемое выражение – Dfd, где Dfd есть сокращение латинского термина «Definiendum», что в переводе на русский язык означает определяемое выражение. Таким образом, в общей практической логике Dfd есть простое общее имя, которому приписывается определенный смысл;

2) Определяющее выражение – Dfn, где Dfn есть сокращение латинского термина «Definiens», что в переводе на русский язык означает определяющее выражение. Таким образом, Dfn есть общее описательное имя, которое, как мы отметили выше, обладает изначальным самостоятельным смыслом и, следовательно, представляет некоторое общее понятие. Мы помним, что понятие есть смысл имени, и в определении как логической операции Dfn приписывается в качестве смысла Dfd.

3) Связка определения. В русском языке роль связки в явных определениях выражает слово «есть». При формализации явных определений простых общих имён связка представляется знаком равенства «=», где знак «=» указывает на то, что класс предметов, мыслимый в качестве значения Dfd, совпадает с классом предметов, мыслимым в качестве значения Dfn. Это обстоятельство позволяет использовать явные определения простых общих имен в качестве правил взаимозаменяемости терминов в суждениях (высказываниях) без изменения их истинностных значений (истина, ложь).

Пример явного определения простого общего имени, где D означает сокращение слова «дефиниция» («определение»).

D: Квадрат (Dfd) есть (=) прямоугольник с равными сторонами (Dfn).

Этот пример показывает, что логическую структуру данного определения можно записать в виде равенства: Dfd=Dfn, что показывает его принадлежность к типу явных определений. Логическую структуру этого определения и, далее, логическую структуру любого явного определения простого общего имени можно также записать в виде Dfd Dfn, где стрелки « » указывают на возможность использования явных определений в качестве правил взаимозаменяемости терминов в суждениях (высказываниях) с учётом того, что класс предметов, мыслимый в Dfd, совпадает с классом предметов, мыслимым в Dfn.

Описанная характеристика явных определений позволяет выделить в общей практической логике их следующие функции:

1) фиксировать смыслы простых общих имен;

2) использоваться в качестве правил взаимозаменяемости терминов в суждениях (высказываниях);

3) использоваться в качестве простого правила дедуктивного вывода в элементарных умозаключениях;

4) вводить в язык рассуждающего ясные понятия.

Так, например, благодаря определению D: квадрат (Dfd) есть прямоугольник с равными сторонами (Dfn) слово «квадрат», являющееся простым общим именем, начинает представлять в языке ясное и точное понятие: «прямоугольник с равными сторонами», что обеспечивает точность рассуждения, в котором фигурирует слово «квадрат».

5) рассматриваться в качестве семантических правил языка либо в качестве суждений.

Продемонстрируем функции 2) и 3) явных определений на следующем примере.

Пусть мы имеем явное определение D: Кража (Dfd) есть тайное хищение имущества или денег (Dfn) и истинное суждение (высказывание) А: «Все кражи есть аморальные поступки» (и). Тогда, используя D в качестве правила взаимозаменяемости терминов, мы можем построить следующее элементарное дедуктивное умозаключение:Все кражи есть аморальные поступки (и), следовательно, Все тайные хищения имущества или денег есть аморальные поступки (и).

В данном умозаключении мы переходим от истинного суждения в посылке к истинному суждению в заключении, используя в качестве простого правила дедуктивного вывода определение D, которое позволяет заменить термин «кража» словосочетанием «тайное хищение имущества или денег» и таким образом получить истинное заключение «Все тайные хищения имущества или денег есть аморальные поступки».

В ТЛ структуру явного определения записывают в виде: А=ВС, где В – родовой признак, буква С – видовое отличие.

6.4. Виды явных определений

Все явные определения делятся в логике на реальные и номинальные. Реальные определения возникают, когда в познании решается задача, как по уже имеющемуся в естественном языке простому общему имени с интуитивно ясной границей его применения найти (сформулировать) его смысл. Ясно, что для этого нужно сначала глубоко исследовать предметы, которые составляют значение анализируемого простого общего имени, чтобы затем сформулировать о них понятие с ясным основным содержанием. Далее нужно приписать полученное понятие в качестве смысла анализируемому простому общему имени, которое в результате данной операции примет статус Dfd, а приписываемое понятие – статус Dfn. В итоге осуществления данных шагов возникнет реальное определение анализируемого простого общего имени, и тем самым благодаря процедуре реального определения в язык общения или исследования вводятся ясные понятия в виде описательных общих имен (Dfn - определений) и в виде простых общих имен (Dfd - определений).

При этом следует иметь в виду следующие обстоятельства.

Во-первых, то, что задача реального определения простых общих имен не является тривиальной, а требует от исследователя способности точного и глубокого познания предметов, составляющих значение определяемого термина, с тем чтобы найденный на этой основе смысл определяемого термина проводил точную границу класса предметов, представляющего значение определяемого термина.

Именно эту трудность иллюстрирует в истории философии известный диалог между Платоном и Диогеном по поводу смысла простого общего имени «человек». Так, когда Платон определил человека как «существо двуногое и беспёрое», Диоген принёс с рынка ощипанного петуха и с иронией произнёс: «Платон, вот твой человек!»

Данная ситуация показывает, что Платон приписал термину «человек» смысл, который неадекватно проводит границу его значения.

Далее известно, что определения можно рассматривать и как семантические правила, т.е. как правила, которые приписывают смысл и указывают на значение языкового выражения, и также рассматривать как суждения. В первом случае они не оцениваются в терминах «истинно», «ложно», во втором случае они оцениваются в данных терминах.

Применительно к реальным определениям это означает, что когда они рассматриваются в качестве суждений о предметах физического мира, то со временем эти определения могут из истинных превращаться в ложные, так как известно, что все физические предметы находятся в пространстве и времени, а всё, что находится в пространстве и времени, вовлечено в процессы изменения и развития. Поэтому прежде чем использовать реальные определения-суждения в качестве аргументов некоторых доказательств и опровержений, предварительно нужно проверить их истинность.

Номинальные определения возникают, когда в познании решается задача: как по уже имеющемуся в языке описательному общему имени, представляющему в языке ясное понятие, подобрать (найти) простое общее имя в качестве вторичного сокращённого представления в языке первичного понятия, представленного в языке описательным общим именем. При этом первичное понятие, представленное общим описательным именем, приобретает в номинальном определении статус Dfn, а простое имя, вторично представляющее в сокращенном виде в языке исходное понятие, приобретает статус Dfd.

Рассмотрим генезис понятия «квадрат». Очевидно, что первоначально древние геометры имели в своём распоряжении понятие «плоская четырёхугольная фигура, у которой все четыре угла прямые и все четыре стороны равны». Это понятие возникло в головах древних геометров на основе описания в языке чистого созерцания данной геометрической фигуры, а затем для краткой формулировки теорем о данной геометрической фигуре (в данной фигуре все диагонали взаимно перпендикулярны; в данной фигуре все диагонали делятся в точке пересечения пополам) геометры на основе свободного соглашения стали употреблять в языке планиметрии вместо общего описательного имени «плоская четырёхугольная фигура, у которой все четыре угла прямые и все четыре стороны равны» простое общее имя «квадрат». Это соглашение они закрепили в языке номинальным определением: квадрат (Dfd) есть плоская четырёхугольная фигура, у которой все четыре угла прямые и все четыре стороны равны (Dfn).

Это определение называется номинальным (от лат. noman – имя; см. Лат.-Русс. словарь Дворецкого), потому что оно как операция (действие) осуществляется лишь на уровне имен (сокращение сложного (описательного) имени простым); при этом сами предметы, составляющие значение описательного имени, не исследуются.

Как и в случае реального определения, номинальные определения также вводят понятия в язык общения либо исследования. Однако в случае номинальных определений речь идёт лишь об этапе вторичного введения понятий в язык посредством замены описательного имени простым, в то время как в реальных определениях понятия вводятся в язык дважды: сначала (первично) в виде описательного общего имени, которое возникает в результате исследования самих предметов, составляющих значение определяемого простого имени, а затем (вторично) в виде простого имени взамен описательного имени, так как исследование показывает, что их значения совпадают.

Так как номинальное определение является результатом свободного соглашения пользователей языка, то в случае, если номинальное определение рассматривается в статусе суждения, то оно квалифицируется как необходимо истинное по соглашению. Следовательно, номинальные определения можно рассматривать в процессах доказательства и опровержения в качестве достоверных аргументов. Поэтому когда в дискуссиях говорят, что об определениях не спорят, то это относится к номинальным определениям. Из описания природы реальных и номинальных определений следует, что реальные определения являются итогом исследования в науках о природе, в то время как номинальные определения являются началом всякого исследования в логико-математических науках. Формально для различения реальных и номинальных определений в записи их логических структур используются следующие нотации. Формальная запись логической формы реального определения: Dfd = Dfn; формальная запись логической формы номинального определения: Dfd = _dfDfn, где знак «df» читается как «равно по определению» («соглашению»).

6.5. Правила явных определений

В общей практической логике фиксируются четыре правила явных определений.

1. Правило соразмерности. Это правило требует, чтобы класс предметов, который мыслится в Dfd, в точности совпадал с классом предметов, который мыслится в Dfn. Формальное выражение данного правила: КDfd = КDfn, где К есть сокращение термина «класс предметов».

При нарушении данного правила возможны следующие ошибки:

а) ошибка широкого определения. Она возникает, когда класс предметов, который мыслится в Dfn, шире, чем класс предметов, который мыслится в Dfd. Формальное выражение ошибки:

КDfd 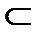КDfn.

Пример ошибки широкого определения. Автомобиль (Dfd) есть транспортное средство с двигателем внутреннего сгорания (Dfn). Это определение является широким, так как в объёме понятия, стоящего на месте Dfn, мыслятся не только автомобили, но и мопеды, мотоциклы, трактора, речные и морские суда, тепловозы и др. транспортные средства. Таким образом, приведенное определение автомобиля не является соразмерным.

б) ошибка узкого определения. Она возникает, когда класс предметов, мыслимый в Dfn, уже, чем класс предметов, который мыслится в Dfd. Формальное выражение ошибки: КDfn 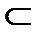КDfd.

Пример ошибки узкого определения. Потерпевший (Dfd) есть лицо, которому причинён физический или моральный ущерб (Dfn). Это определение является узким, так как известно, что к потерпевшим относят ещё лиц, которым причинён имущественный ущерб.

Выполнение правила соразмерности определения является необходимым условием адекватного познания. Если же это правило не соблюдено, то при использовании такого определения в качестве правила взаимозаменяемости терминов в некотором суждении возможен переход от истины ко лжи, т.е. становится возможным нелогичное рассуждение, и процесс достижения истины затрудняется.

Очевидно также, что сферой действия данного правила являются реальные определения. Ибо эти правила предполагают нахождение границы множества предметов, мыслимых в Dfd, в результате исследования признаков предметов, которые отбираются в объём понятия, занимающего в определении место Dfn. Для номинальных определений это правило выполняется автоматически.

2. Правило исключения круга из определения.

Под кругом в определении понимается такой его вид, когда определяемое выражение (Dfd) пересказывается в определяющем выражении (Dfn) с точностью до грамматики. Данное правило требует исключения круга из определения.

В общей практической логике принято различать явные и неявные круги в определениях. Явный круг принято называть тавтологией, а неявный круг можно называть скрытой тавтологией. Наличие круга в определении является логической ошибкой, так как определения с кругами либо малоинформативны, либо неинформативны.

Пример явного круга (тавтологии) в определении. Масло (Dfd) есть маслянистое вещество, которое применяется в пищевых либо технических целях (Dfn). Это определение малоинформативно, так как в нём смысл слова «масло» не раскрывается в Dfn, а пересказывается с точностью до грамматики, что означает, что в Dfd оно является существительным, а в Dfn является прилагательным.

Неявные круги в определениях обнаруживаются при сравнении двух определений. Пример*. Пусть некто утверждает, что вращение тела (Dfd) есть его движение вокруг оси (Dfn), а на наш вопрос: что такое ось? – отвечает, что ось (Dfd) есть линия, вокруг которой происходит вращение тела (Dfn). Тогда, подставив в первое определение вместо слова «ось» выражение «линия, вокруг которой происходит вращение тела», т.е. Dfn второго определения, получим явную тавтологию: вращение тела есть его движение вокруг линии, вокруг которой происходит вращение тела. Таким образом, вращение в данном случае определяется через вращение, что является уже открытой тавтологией, или явным кругом в определении.

3. Правило ясности определения. Его формулировка: определение должно быть ясным.

Это правило требует:

1) чтобы в определяющем выражении, т. е. в Dfn, использовались либо слова с интуитивно ясным значением, либо слова, для которых в языке уже приняты определения.

Так, например, очевидно, что определение: остров (Dfd) есть часть суши, окруженная со всех сторон водой (Dfn), удовлетворяет требованию ясности, в то время как определение**: «Ализарин (Dfd) есть красящее вещество марены» (Dfn) не будет удовлетворять требованию ясности до тех пор, пока не будет определён термин «марена».

2) В определяющей части (Dfn) определения не должны использоваться художественно-образные языковые средства в виде метафор. Поэтому такие контексты, как «Праздность есть мать всех пороков», «Артиллерия есть бог войны» и другие пословицы и поговорки обычного языка, нельзя квалифицировать в статусе определений, так как их определяющие выражения приписывают определяемому выражению не прямые, а переносные смыслы. Ясно, что замена этих выражений друг на друга в некотором рассуждении сделает это рассуждение путаным и невнятным***.

3) В определяющей части, т.е. в Dfn, не должны использоваться лишние слова.

Так, определение: «Закон (Dfd) есть необходимая, всеобщая, устойчивая и повторяющаяся связь между явлениями (Dfn)» не удовлетворяет требованию ясности. В его Dfn используются такие лишние слова, как «устойчивая, всеобщая и повторяющаяся связь», которые загромождают определяющее выражение, т.е. Dfn. Ведь известно, что если связь является необходимой, то она устойчива, всеобща и повторяема (8, с. 224).

Резюме: неясные определения нельзя использовать в качестве правил взаимозаменяемости терминов.

4. Правило неотрицательности. Оно имеет следующую либеральную формулировку: определение по возможности не должно быть отрицательным. Это правило требует, чтобы в общении и исследованиях мы по возможности избегали отрицательных определений, так как отрицательные определения малоинформативны: они сообщают нам информацию, чем нечто не является, и не сообщают нам информацию, чем нечто является. Например, очевидно, что определение:* «Республика есть форма государственного правления, которая не является монархией» не несёт позитивной информации о республике, и потому данное определение малопродуктивно как в актах общения, так и в исследовательской деятельности.

Однако уместность либеральной оговорки «по возможности определение не должно быть отрицательным» объясняется тем, что в некоторых практических ситуациях отрицательные определения могут быть достаточно эффективными. Так, определение** «бесхозное имущество (Dfd) есть имущество, которое не имеет собственника» (Dfn) может быть достаточно эффективным в юридической практике.