Занятие 2. Изгибаемые элементы прямоугольного профиля

Прочность нормальных сечений с одиночной арматурой.

Сечения прямоугольного, таврового и двутаврового профилей с арматурой, расположенной у перпендикулярных плоскости изгиба граней при действии момента в плоскости симметрии сечения допускается производить по предельным усилиям. Расчет прочности по нормальным сечениям заключается в определении необходимого количества растянутой арматуры, в предположении, что прочность бетона сжатой зоны и продольной растянутой арматуры в рассматриваемом сечении будет исчерпана одновременно.

Граничное зна­чение относительной высоты сжатой зоны ξ_R определяют по эмпирической формуле, полученной на основе статистической обработки многочисленных данных опытных исследований зависимости. Для элементов без предварительного напряжения арматуры граничная относительная высота сжатой зоны определяется по формуле.

ξ_R = 0,8/(1+R_s/700).

Здесь R_s- расчетное сопротивление арматуры в МПа.

Прочность рассчитывают на уси­лия, полученные из статического расчета железобетонных конструкций на воздействие расчетных нагру­зок.

Пример расчета

Пример 2.1. Выполнить расчет прочности сечения с одиночной арматурой. Размеры сечения b×h = 40×140см, бетон В20; R_b =11,5 МПа, (11,5·10³ кН/м²); рабочая арматура класса А400, R_s =355 МПа, (355·10³ кН/м²); в сечении действует расчетный момент (с учетом кратковременных нагрузок) М = 600 кНм. Предварительное расположение стержней в один ряд, а=4 см.

Рабочая высота сечения h_o=h – а = 140 – 4 = 136 см=1, 36 м.

Граничная высота сжатой зоны при арматуре А400

ξ_R =0, 531, α_R = 0,39.

Вычисляется коэффициент α_m

α_m = М / R_bbh_o² = 600 / 11,5·10³ ·0,4·1,36² = 0,0705.

α_m = 0,0705< α_R = 0,390.

а = 60

b = 400

а2 =310

a6 =334

аt=15

ц.т

dw=8

Рис. 2.1. Армирование сечения изгибаемого элемента к примеру 2.1. 1 –2Ø22 А400 АS = 7,6 см2, 2–2Ø20 А400 АS = 6,28 см2, 3–2Ø10 А400 А/S = 1,57 см2, 4–AS1= 0,1·0,25h·0,5b = 0,7 см2. 1Ø10 А400 AS1=0,785 см2.

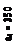
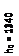
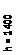
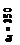
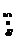
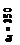
Сжатая арматура по расчету не требуется.

Вычисляется площадь растянутой арматуры

A_s=R_bbh₀ (1-√1-2α_m)/R_s =11,5·10³ ·0,4·1,36(1-√1- 2·0,0705)/355·10³ ≈ 0,00129 м² =12,9 см².

В соответствии с сортаментом принимаем

2Æ20+2Æ22 А400 с площадью А_s = 6,28+7,6 = 13,88 см².

При размещении арматуры в два ряда рабочая высота сечения уменьшится и будет равна, см. рис. 2.1.

h_o= h – а-Ø/2-а₁ /2=140 – 4 –22/2 –25/2 = 133,5см ≈134,0 см=1, 34 м,

где а₁ – минимальное расстояние между продольными стержнями а₁= 25мм.

Уточним расчет при h_o = 1,34 м.

α_m = М / R_bbh_o² = 600/11,5·10³ ·0,4·1,34² = 0,0726.

α_m = 0,0726 < α_R = 0,390.

Сжатая арматура по расчету не требуется. Уточняем площадь растянутой арматуры

A_s= R_bbh₀(1-√1 -2α_m)/R_s = 11,5·10³ ·0,4·1,34(1-√1-2·0,0726)/355·10³ =0,00131 м² =13,1 см² .

В соответствии с сортаментом принимаем

2Æ20 + 2Æ22 А400 с площадью А_s= 6,28+ 7,6 =13,88 см².

Перерасход арматуры составляет (13,88 –13,1)·100/13,1 = 5,95%.

Процент армирования сечения

μ=100A_s/ bh_o=100·13,1/40·134 = 0,244% > μ_min = 0,1%.

Схема армирования сечения представлена на рис. 2.1.

Задание. 2. В соответствии с данными таблицы 1 выполнить расчет прочности нормального сечения прямоугольного профиля с одиночной арматурой. Законструировать сечение с соблюдением конструктивных и нормативных требований. Выполнить чертежи армирования в масштабе 1:10 или 1:25.

Рис.2.2. Армирование сечений к примеру 2.2. 1–4Ø18А400 АS=10,18 см2, 2–2Ø10 А400 А/S=1,57 см2, 3–4Ø10 А400 АS1=3,14 см2

б)

b = 300

а2 =218

а6 =234

аt=15

ц.т

а = 60

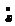
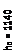
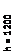
Пример 2.2.Выполнить проверку прочности нормального сечения элемента. Размеры поперечного сечения b× h=30×120 см. Тяжелый бетон класса В25; R_b =14,5МПа, (14,5·10³ кН/ м²); рабочая арматура - стержни 4Æ18 А400 с площадью А_s= 0,18 см² = 0,001018 м², R_s= 355 МПа, (355·10³ кН /м² ); в расчетном сечении действует внешний изгибающий момент от всех нагрузок, включая кратковременные, М = 350 кНм, а= 6 см.

Рабочая высота сечения h_o=h –а=120 – 6 =114см=1,14 м.

Положение нейтральной оси, значение «х»

х = R_s A_s/R_bb = 355·10³ · 0,001018 / 14, 5·10³·0,3 = 0,0831м = 8,31см.

Для арматуры А400 находим ξ_R = 0,531, α_R = 0,390.

ξ = х/h₀ = 8,31/114 = 0,0729 < ξ_R = 0,531.

Проверка прочности нормальных сечений с одиночной арматурой производят при ξ ≤ ξ_R из условия

М_сеч= R_sA_s(h₀ – 0,5х) = 355·10³ ·0,001018 (1,14 – 0,5·0,0831) =396,96 кНм.

М = 350 кНм ≤ М_сеч= 396,96 кН·м.

Условие прочности выполняется, прочность сечения достаточна.

Коэффициент армирования сечения

μ = A_s/ b·h_o = 10,18/30·114 = 0,00297, (0,3%) > μ_min = 0,1%.

Схема армирования поперечного сечения представлена на рис. 2.2.

Таблица 2.1

№	Момент	Высота сечения h	Ширина сечения b	Класс бетона	Класс арматуры
кНм	см	см
				В25	А400
				В25	А400
				В25	А400
				В25	А400
				В25	А400
				В25	А400
				В25	А400
				В30	А500
				В30	А500
				В30	А500
				В30	А500
				В30	А500
				В30	А500
				В30	А500
				В30	А400
				В30	А400
				В30	А400
				В30	А400
				В30	А400
				В30	А400
				В35	А400
				В35	А500
				В35	А500
				В35	А500
				В35	А500

3. Занятие 3. Изгибаемые элементытаврового профиля.