Предмет логики. Исторические этапы формирования логики.

Понятие языка, знака, семиотические аспекты языка. Естественный и искусственный язык. Объектный язык и метаязык.

Язык– это знаковая система, предназначенная для фиксации, переработки и передачи информации от одного субъекта к другому.

При создании языка основным элементом являются знаки. Знаком называется тот объект, который для некого субъекта выступает в качестве представителя какого-то другого предмета.

Выделяют несколько видов знаков:

1) знаки-копии (фотографии, отпечатки пальцев и т. п.);

2) знаки-признаки (дым – признак огня, боль – признак болезни и т. п.);

3) знаки-сигналы (звонок – начало занятия);

4) знаки-символы (дорожные знаки, буквы алфавита и т. п.).

Изучение любого языка может осуществляться в трех аспектах – синтаксическом, семиотическом и прагматическом.

Под семантикой понимают исследование отношений между знаками и обозначаемыми предметами т.е. исследование значений и смыслов знака. При это абстрагируются от отношений знаков к носителям языка (интерпретаторам). Здесь решаются различные задачи и, в частности, задача выделения различных категорий (типов) знаков в зависимости от типов их значений, а также от типов выражаемых этими знаками смыслов.

Различаются несколько видов языков. Прежде всего языки подразделяются на естественный и искусственный язык. Естественныеязыки возникли как средство общения между людьми (национальные устные и письменные языки, язык танцев, жеста, мимики). Их процесс формирования длительный, стихийный, не подчиняющийся нормативной регламентации. Искусственный создается человеком для решения определенных задач (язык шахматных нотации, химической формулы, язык программирования).

Объектным языком называется тот язык, который является предметом исследования, а метаязык – тот, с помощью которого изучается объектный язык.

3.Семантические категории языковых выражений: предложения и термины. Дескриптивные и логические термины.

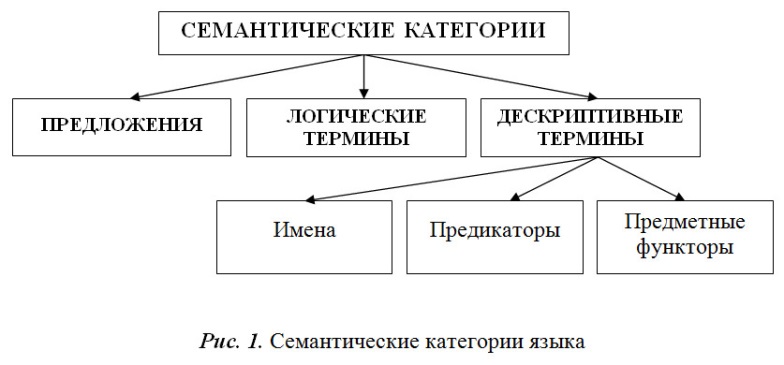
Семантическая категория – это класс выражений с однотипными предметными значениями, при этом включающий все выражения с предметным значением данного типа.

Такими классами являются имена, предикаторы, предметные функторы, логические термины, повествовательные предложения.

Логические термины (логические константы) – это знаки логических отношений «и», «или», «если…, то…», «неверно, что» и операций «всякий», «существует» («некоторые»), «тот…, который…».

Знаки первых четырех категорий (имена, предикаторы, предметные функторы и логические термины) используются в составе предложений. При этом, в отличие от логических терминов, имена, предикаторы и предметные функторы называются дескриптивными (описательными) терминами

Дескриптивные и логические термины различаются тем, что первые специфичны для различных областей познания и поэтому характеризуют конкретное содержание высказываний той или иной области познания. Логические термины являются общими в высказываниях разных областей познания и определяют те аспекты смыслов высказываний, понятий, теорий, которые называют логическими содержаниями.

Имена, смысл и значение имен. Карнаповские принципы теории именования. Антиномии теории именования. Экстенсиональный и интенсиональные контексты.

Имена, их смысл

Имена — это необходимое средство познания и общения. Имена и вещи, с которыми они связаны, естественны, причем настолько, что когда-то они казались принадлежащими самим вещам, подобно цвету, тяжести и т.п.

Роль имен в языке велика, иногда в науке о языке придание имен вещам считается чуть ли не единственной задачей языка. Все без исключения науки, изучающие язык, занимаются исследованием имен как одного из основных понятий. В их числе логика, для которой имя — одна из основных семантических категорий.

Структура предложения дает возможность определить имя по его роли в этом предложении. Выражение языка, выступающее как подлежащее или именная часть сказуемого в простом предложении «S есть Р> (где S — подлежащее, Р— сказуемое), становится именем. Скажем, «Сталин», «Король Артур» и «человек, открывший Америку» — это имена, поскольку подстановка их вместо букв S и Р дает осмысленные предложения: «Сталин есть человек, открывший Америку», «Король Артур есть человек, открывший Америку», и т.п.

Один-единственный предмет обозначает единичные имена. Общие имена обозначают более чем один предмет. Например, имя «Солнце» единичное, оно обозначает единственную звезду в Солнечной системе. К общим именам относятся, например, имена «человек», «профессор», поскольку эти имена связаны с множествами (классами) предметов, причем имя относится не к множеству как единому целому, а к каждому входящему в него предмету. Слово «человек» обозначает не всех людей вместе, а каждого, о ком можно сказать: «Это человек». Слово «человечество» не общее, а единичное имя, поскольку объект, называемый «человечеством», всего один.

Отметим понятия как общие имена, имеющие особое значение. Понятие является общим именем с ясным и устойчивым содержанием, которое употребляется в обычном языке или в языке науки. Не существует строгой границы между теми именами, которые можно назвать понятиями, и теми, которые не относятся к понятиям.

Имя «понятие» используется и в повседневном, и в научном языке. Единства мнений в истолковании содержания этого имени нет. В одних случаях под «понятиями» имеют в виду все имена, включая и единичные. Понятиями являются не только «море» и «треугольник», но и «самое соленое море», и «равнобедренный треугольник». Понятия могут пониматься как общие имена, отражающие предметы и явления в их существенных признаках. Иногда происходит отождествление понятия с содержанием общего имени.

Имена делятся на пустые (или беспредметные) и непустые. Пустое имя по определению не обозначает ни одного существующего предмета. Имя, не являющееся пустым, обозначает, по крайней мере, один реальный объект.

К пустым, например, относятся имена «Прометей», «кентавр», созданные мифологией. Используемые в физике и математике и обозначающие идеализированные имена также являются пустыми («несжимаемая жидкость», «точка»). Физические тела или живые существа обозначаются конкретными именами.

Формализованный язык классической логики высказываний. Определение формулы и подформулы формулы. Таблицы истинности. Классификация формул по условиям истинности. Сокращенные таблицы истинности, их назначение.

Формализованный язык классической логики высказываний.

Формализованный язык классической логики предикатов является фрагментом и результатом некоторой реконструкции естественного языка. Специфика его состоит, прежде всего, в наличии точных правил построения высказываний (формул) и сложных имен (термов). Этот язык предназначен для аксиоматического построения теорий, для анализа содержания высказываний естественного языка и выявления логических отношений между ними, для описания правил рассуждения, построения выводов и доказательств и т.д.

Формальный язык логики высказыванияч состоит из выражений сдледующих групп:

1. Потенциального бесконечного списка элементарных высказываний (р_1…p_n, q₁…q_n и так далее)

2. Логической связки (константы)
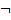- логическое отрицание («не» или «неверно, что»);
˄ - конъюнкция («и»);
v - дизъюнкция («или»);
Ú - строгая дизъюнкция («либо…, либо…»);
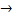- импликация («если…, то…»);
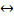- эквивалентность («тогда и только тогда, когда…»);

3. Технических связок. Скобки и запятая.
Формулами логики высказываний называются

1) атомарные формулы;

2) выражения вида (F) ˄ (G), (F) v (G), ⌐(F), (F)→(G), (F)↔(G), где F и G –

формулы логики высказываний.

Подформулой атомарной формулы является она сама. Подформулами формулы ⌐F являются формула ⌐F и все ее подформулы. Подформулами формул (F) ˄ (G), (F) v (G), (F) ↔G являются они сами и все подформулы формул F и G.

Таблицы истинности определяют условия истинности для сложных высказываний при условии, если элементы высказывания даны (предварительно) истинные значения.

2ⁿ – количество строк в таблице, где n – число различных высказываний.

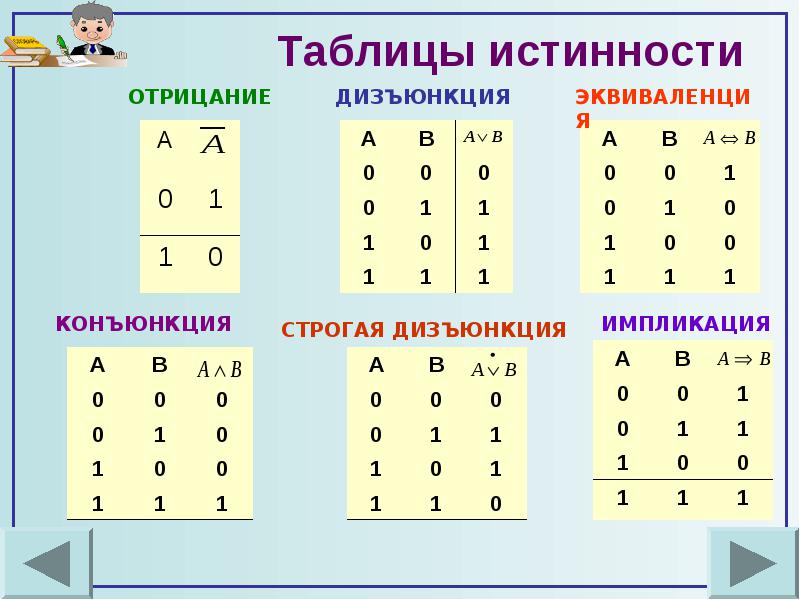
Классификация формул по условиям истинности.

Формула называется выполнимой, если некоторая ее конкретизация является истинным высказыванием
Формула называется тождественно истинной, если любая ее конкретизация является истинным высказыванием.
Формула называется опровержимой, если некоторая ее конкретизация является ложным высказыванием.
Формула называется тождественно ложной, если любая ее конкретизация является ложным высказыванием.
Для того чтобы определить, к какому типу относится формула, достаточно составить для нее таблицу истинности.

Сокращенные таблицы истинности, их назначение.
(Или сокращенный метод проверки общезначимости формул, или метод от противного)

1. Допустим, что формула не общезначима (т.е. в результате в столбце есть нуль).

2. Распределяем значения простых формул данной формулы.

3. Если встречаем противоречия (т.е. в одной и той же атомарной формуле принимается одновременно значение истинности 1 и ложности 0), то наше предположение, что формула необщезначима является неверным (т.е. формула общезначима)

4. Если противоречий нет, то наше предположение верно, формула необщезначима.

Требование к адекватной формализации класса общезначимых формул и отношение логического следования; корректность, полнота, непротиворечивость. Разрешимость классической логики высказываний.

Формализация – даны отправные точки, истинные определения, посылки.
Для аксиоматизации логического высказывания и логики предикатов требуются:

1. Создать формальный язык и все сопутсвующие понятия типа правильно построенная формула, подформула и т.п

2. Указать определение доказательств и доказуемой формулы на основе правила

3. Формулировка формул, правил и доказательств

4. Сформулировать относительно данной системы метод требования

5.Корректность и полнота- Требование должно полно и точно описывать функцию, которую необходимо реализовать в продукте, содержать всю необходимую для разработчиков информацию. Контроль над корректностью требований возлагается на пользователей, т.к. только требование, согласующееся с источником (пожеланиями пользователей) считается корректным.

6. Разрешимость, непротиворечивость

Формула является разрешимой если у нас есть общий метод доказуемости формул.

Логика высказываний разрешима, т.к посредством истинности мы всегда можем проверить является ли формула общезначимой, но тогда по теореме полноты мы можем сказать, что формула разрешима относительно доказуемости.

Терм

1. Произвольная предметная константа ( напр. a)

2. Произвольная предметная переменная (напр. t1)

3. Если Ф – n-местная, предметно функциональная константа, а t1,t2….tn термы. То выражение Ф(t1,t2….tn) является термом.

4. Ничто иное не является термом

1,2 – простые термы; 3- сложные

! Терм не может начинаться с предикаторной константы в виде P (g(x, a)) и не может начинаться с двухместной константы напр. h(g(x,a). Хотя я не особо понимаю и мне кажется проблема везде в двойной формуле, то сеть g (x, a) – терм

Подформулой атомарной формулы является она сама. Подформулами формулы F являются формула F и все ее подформулы. Подформулами формул F&G, FvG, F→G, F↔G являются они сами и все подформулы формул F и G.

Определение формулы

1. Если П-N местная предикаторная константа, t1,t2….tn-это термы, то выражение П(t1,t2….tn) является формулой

2. Если А- формула, то L(представим что то отрицание)А-формула

3. Если А и В –формулы, то (А^В) и т.п-формулы

4. Если А формула, а а- предметная переменная, то VаА является формулой

5. Ничто иное не является формулой

Формулы типа 1 – элементарные, атомные; другие формулы- сложные, молекулярные

Логическое следование – отношение, существующее между посылками и обосновано выводимыми из них заключениями (напр. Если А, то В)

Понятие модели.

Модель – есть упорядоченная двойка объектов, в которой <D;Y>D – не пустая область объектов, а Y – функция, сопоставляющая дисприктивные выражения языка, некоторые объекты в области D.

! Важно то, что они истинные

Требования к адекватной формализации общезначимых формул и отношения логического следования: корректность непротиворечивость и полнота исчисления предикатов. Проблема разрешимости.

Содержательные	Формальные

Простое категорическое суждение- простое суждение, в котором что-то утверждается и отрицается относительно предмета мысли, а между субъектом и предикатом устанавливается категорическая (утвердительная, отрицательная) связь: отношение тождества, подчинения, частичного совпадения, противоречия, противоположности, соподчинения

Структура простого категорического суждения: состоит из субъекта, предиката, связки.

Классификация

I. По качественному признаку (характеру связки), простые категорические суждения делятся на утвердительные и отрицательные.

В утвердительных суждениях говорится о наличии свойства у предмета и принадлежности предмета субъекту: S есть Р.

Отрицательные суждения говорят об отсутствии свойств у предмета: S не есть Р, или S есть не Р.

II.По количественному (объемному) показателю, выражаемому квантором, простые категорические суждения делятся на единичные, частные и общие.

Единичное суждение :субъект суждения - единичное понятие (название города).

Частное суждение- совокупность предметов, но не вся, подчеркивается квантором: «Некоторые S есть Р». В количественном отношении частные суждения неопределенны.

Общее суждение о всей предметной области, на которую направлено внимание. Суждение с квантором (все, ни один, каждый, без исключения) перед субъектом: «Все S есть Р».

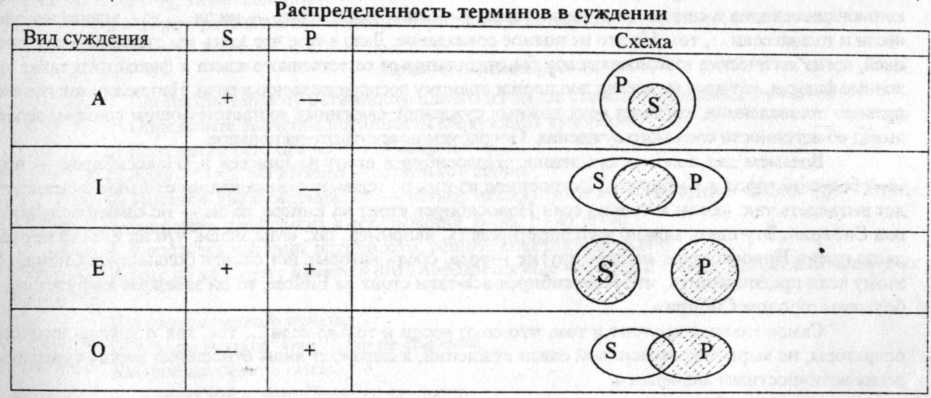
СООТНОШЕНИЕ ОБЪЕМОВ ТЕРМИНОВ: исходя из количественной классификации можно определить распределенность терминов в суждении ( чтобы понимать смысл суждений, строить умозаключения, надо знать, как относятся субъект и предикат суждения. Для выражения отношений субъекта и предиката используют операцию распределения терминов в суждении)

Формальнологический анализ этих суждений выявляет структурные закономерности их, не зависящие от содержания. Исходя из структуры общих (утвердительного и отрицательного) суждений можно, не зная содержания, сказать, что их субъекты взяты в полном объеме (для отрицательного - в полном объеме исключаются из рассмотрения). КОРОЧЕ: благодаря этому нам пофигу на смысл высказывания. В дальнейшем, не затрачивая кучу времени на размышления, люди делают выводы просто подставляя термины в эти схемы-кружочки ,проводя с ними не хитрые махинации .Будучи философом я могу проверить вывод химика, не понимая о чем идет речь вовсе.

Непосредственными умозаключениями называются дедуктивные умозаключения, делаемые из одной посылки. К ним относятся следующие: превращение обращение, противопоставление предикату и умозаключения по «логическому квадрату»

· Превращение - вид непосредственного умозаключения, при котором изменяется качество посылки без изменения ее количества. (Напомню по качеству связки категорические суждения делятся на утвердительные и отрицательные) При этом частноутвердительное суждение превращается в частноотрицательное и наоборот, а общеутвердительное суждение - в общеотрицательное и наоборот.

Для превращение необходимо в исходное суждение вставить два отрицания: перед связкой и перед предикатом.

Превращению подлежат все 4 вида суждения: А, Е,I,О.

1. А-Е.

Структура: все S есть Р.- ни одно S не есть не -Р.

Все волки - хищные животные. - ни один волк не является нехищным животным.

2. Е-А.

Ни одно S не есть Р. - все S есть не -Р.

Ни один многогранник не является плоской фигурой. - все многогранники не являются неплоскими фигурами.

3. I -О

Некоторые S есть Р. - некоторые S есть не -Р. Некоторые грибы съедобны. Некоторые грибы не являются несъедобными.

4.О - I. Некоторые S не есть Р. - некоторые S есть не -Р. Некоторые члены предложения не являются главными. - некоторые члены предложения являются неглавными.

КОРОЧЕ: меняете букву на противоположную (A-E, E-A, I-O,O-I.) ,а к «p» добавляете отрицание (черточка сверху)

· Обращениемназывается такое непосредственное умозаключение, в котором в заключении субъектом является предикат, а предикатом - субъект исходного суждения, т.е. происходит перемена мест субъекта и предиката при сохранении качества суждения.

• Общеутвердительные суждения обращаются в частноутвердительные
• Общеотрицательные суждения обращаются в общеотрицательные суждения
• Частноутвердительные суждения обращаются в частноутвердительные суждения
• Частноотрицательные суждения не обращаются совсем

Примеры:

1. все дельфины -млекопитающие. - некоторые млекопитающие являются дельфинами.

2. все развернутые углы - углы, стороны которого составляют одну прямую. -все углы, стороны которого составляют одну прямую, являются развернутыми углами.

3. некоторые школьники являются филателистами - некоторые филателисты являются школьниками.

4. некоторые музыканты - скрипачи. - все скрипачи являются музыкантами.

Обращение бывает 2-х видов: простое или чистое (примеры 2 и3) и обращение с ограничением (примеры 1 и 4).

Обращение будет чистое, или простое, тогда когда и S, и Р исходного суждения либо оба распределены, либо оба не распределены. Обращение с ограничением бывает тогда, когда в исходном суждении субъект распределен, а предикат не распределен, или наоборот, S не распределен, а Р распределен.

· Противопоставление предикату.

Это такое непосредственное умозаключение, при котором в новом суждении субъектом является понятие, противоречащее предикату исходного суждения, а предикатом является субъект исходного суждения, вместе с этим связка меняется на противоположную.

Противопоставление предикату можно рассматривать как результат 2- х последовательных непосредственных умозаключений - сначала превращение, затем обращения превращенного суждения. Превращение-обращение

Например, дано суждение: «все львы -хищные животные». В результате противопоставления предикату получим суждение: «ни одно нехищное животное не является львом

Противопоставление предикату для различных видов суждений осуществляется так:

1. А. все S есть Р.--ни одно не -Р не есть S. Все металлы электропроводны. - ни один не электропроводник не является металлом.

2. Е. ни одно S не есть Р. - некоторые не Р есть S.ни один красный мухомор не является съедобным грибом - некоторые несъедобные грибы есть красные мухоморы.

3. О. некоторые S не есть Р.- некоторые не Р есть S. Некоторые преступления не являются умышленными. -некоторые неумышленные деяния являются преступлениями.

4. I. Из частноутвердительного суждения необходимые выводы не следуют.

Противопоставление субъекту – это такоенепосредственное умозаключение, в результате которого в заключении субъектом становится предикат исходного суждения, а предикатом – понятие, противоречащее субъекту исходного суждения.

Структура

Термин, соответствующий субъекту заключения, называется меньшим термином. (S)

Термин, соответствующий предикату заключения, называется большим термином. (P)

Меньший и больший термины называются крайними терминами, они обозначаются соответственно буквами S и P.

Общий термин, присутствующий в обеих посылках, но отсутствующий в заключении, называется средним. Его принято обозначать буквой M (лат. medio – средний).

Посылка, в которой находится меньший термин, называется меньшей посылкой. Посылка, в которой находится больший термин, называется большей. Большую посылку принято ставить первой.

Проверка правильности рассуждений может быть упрощена с помощью фигур простого категорического силлогизма. По месту расположения среднего термина различают четыре фигуры:

Любой простой силлогизм состоит из трёх суждений. Каждое из них является простым и принадлежит к одному из четырех видов(A,I,N,E).Набор простых суждений ,входящих в силлогизм называется модусом простого силлогизма.

Например, модус нижеследующего сил. – ААА(так как все суждения здесь общеутвердительные)

Как я поняла ,модус – конкретный силлогизм одной из фигур.

Во всех четырёх фигурах силлогизмов насчитывается 256 модусов. В каждой фигуре насчитывается 64 модуса. Однако из всех этих 256 модусов только 24 дают достоверные выводы. Это те модусы, для которых между посылками и заключением существует отношение логического следования. Эти 24 модуса называются правильными. Остальные модусы приводят к вероятностным выводам и называются, соответственно, неправильным

Для проверки правильности С. имеется специальный перечень правил.Выполнение каждого правила является необходимым, а всех вместе — достаточным условием, чтобы считать некоторый модус правильным. Эти правила называются общими правилами С. и подразделяются на правила терминов и правила посылок.
Правила терминов:
1. Должна быть посылка, в которой средний термин распределен.
2. Если термин распределен в заключении, то он распределен и в посылке.
Правила посылок:
3. Должна иметься утвердительная посылка.
4. Если утвердительными являются обе посылки, то заключение — утвердительное высказывание
5. Если имеется отрицательная посылка, то заключение — отрицательное высказывание.

Производные правила посылок:

1.Хотя бы одна посылка должна быть общей.

2.Если одна из посылок частная, то заключение тоже будет частным.

Силлогизм считается корректным, если все правила соблюдены.

Возможны два способа проверки корректности силлогизма : вышеперечисленные правила и диаграмма(у всех должен быть в тетради алгоритм(кружочки сравниваем) ).Если нет – пусть кто-нибудь скинет конспект.

ПОДТВЕРЖДЕНИЕ СЛЕДСТВИЙ

В науке, да и не только в ней, непосредственное наблюдение того, о чем говорится в проверяемом утверждении, редкость.

Наиболее важным и вместе с тем универсальным способом подтверждения является выведение из обосновываемого положения логических следствий и их последующая опытная проверка. Подтверждение следствий оценивается при этом как свидетельство в пользу истинности самого положения.

В индуктивных рассуждениях устанавливается логическая связь между индуктивными подтверждениями (посылками) А,,..., Ап и индуктивным предположением (заключением) Т, которую можно выразить в записи: Ая ..., Ап=» Т, где =» — знак индуктивного следования. Индуктивное и дедуктивное следование находятся в отношении обратной связи: если А., .... А =gt; Т, то Т=»А„ ..., Т=»А . Эта связь
I7 7 п 7 I7 7 п
наиболее очевидна для обобщающей индукции. Действительно, из гипотетического предположения Гольдбаха о том, что любое четное число разлагается на сумму двух простых чисел, дедуктивно следует утверждение, что, скажем, число 20 разлагается на сумму двух простых чисел (20 = 13 + 7). Но данное дедуктивное следствие является в то же время индуктивным подтверждением рассматриваемой гипотезы. Таким образом, логический контроль за индуктивными рассуждениями сводится к подтверждению либо опровержению дедуктивных следствий, вытекающих из сделанного индуктивного предположения.
Проверка корректности индуктивного рассуждения основывается на двух схемах рассуждений, одна из которых является доказательной и служит для опровержения индуктивного предположения, а другая — эвристической, подтверждающей правдоподобность сделанного индуктивного предположения.

Итак, в индуктивном рассуждении подтверждение нового следствия имеет большее или меньшее значение в зависимости от того, более или менее это новое следствие отличается от ранее подтвержденных следствий.

Подтверждение наиболее неожиданного следствия является наиболее убедительным.
До сих пор мы рассматривали случаи индуктивных рассуждений, в которых индуктивные подтверждения являлись дедуктивными следствиями индуктивного предположения. Такого типа рассуждения характерны для операции и индуктивного обобщения. Изменим несколько рассматрачаемую ситуацию.
Допустим, требуется опровергнуть предположение Т. Попытка его дедуктивного опровержения, то есть доказательства -іТ, не принесла успеха, но в процессе анализа выяснилось, что предположение Т является дедуктивным следствием из общего основания А, относительно которого можно сказать определенно, истинно оно или ложно. Тогда возможны две схемы логического контроля за рассуждением — дедуктивная и индуктивная.
Доказательная схема Эвристическая схема подтверждения опровержения
А=gt;Т А истинно Т истинно
Л=gt;Т А ложно Т менее правдоподобно
Итак, когда основание, подтверждающее индуктивное предположение, опровергается, степень правдоподобности данного предположения в индуктивном рассуждении уменьшается.
Исследуем два противоречивых предположения Тх и Т2, соперничающих между собой. С точки зрения классической логики ясно, что если Тх истинно, то Т2 ложно, и наоборот. В научно-исследовательской практике этот ответ не столь однозначен, так как здесь принцип двузначности не всегда предполагается; поэтому конкурирующие гипотезы скорее несовместимы, то есть не могут быть совместно истинными, чем противоречивы. Если доказано, что одно из предположений, скажем, Тх истинно, то, конечно, гипотеза Т2 опровергается. Однако, если ложно, то Т2 может быть и истинным и ложным, но, скорее всего, истинным, так как данные два предположения конкурируют между собой. Таким образом, имеются две схемы рас- суждений.

Эвристика – теория правдоподобных рассуждений.

Индуктивное обобщение – это логическая операция, в результате которой на основе фиксированных характеристик, общих для изученных объектов или событий определенного класса, делается вывод о принадлежности данных характеристик всему классу в целом.

Предмет логики. Исторические этапы формирования логики.

Логика - нормативная наука о формах, законах и приемах интеллектуальной познавательной деятельности, осуществляемая с помощью языка.

Логика – наука о законах и формах человеческого мышления, рассматриваемого как средство познания окружающей действительности. Значение логики состоит в следующем:

1) логика выступает важнейшим средством формирования убеждений (прежде всего научных). Эти убеждения опираются на доказательные процедуры своего представления и обоснования. Именно в этом плане логика применялась даже средневековыми схоластами, пытавшимися придать христианскому вероучению рациональную форму, что послужило формальной предпосылкой возникновения действительной науки, отказавшейся от теологических подходов;

2) формальная логика применяется в науке и технике. При этом техническими приложениями формальной логики являются: исчисление высказываний и исчисление предикатов. Без исчисления предикатов не могли появиться искусственные информационные языки, основа современной компьютерной техники. Традиционная формальная логика остается важнейшим логическим инструментом построения доказательств, обоснований во всех науках; 3) традиционная формальная логика остается важнейшим средством в сфере всех видов образования. Она является основой организации всех видов знания для его подачи в процессе обучения; 4) логика является важнейшим и незаменимым инструментом развития культуры. Без логики не может обойтись никакая культурная деятельность вообще, поскольку в ней присутствуют и играют принципиальную роль рациональные элементы.

В своем развитии логика прошла два этапа:

1) с IV в. до н. э. до XIX в. н. э. В этот период произошло возникновение формальной логики, автором которой традиционно считается Аристотель, и ее медленное совершенствование;

2) с конца XIX в. до наших дней произошла научная революция и на смену аристотелевской логике пришла современная.

Отдельные логические проблемы возникали перед человечеством уже свыше 2,5 тыс. лет назад в Древней Индии. В индийской логике много внимания уделяется теории умозаключения, которое в ней отождествляется с доказательством. Логика в Древней Индии не рассматривалась как система, а трактовалась в виде кратких афоризмов. При этом логика была полностью зависима от других наук. Логика Древней Индии была практически неизвестна в Западной Европе.

Поэтому считается, что логические проблемы получают свое освещение только в Древней Греции и Риме.

Основными причинами возникновения логики как науки являются:

1) зарождение и развитие наук. Логика и пыталась выявить и объяснить те требования, которымдолжно удовлетворять научное мышление, чтобы его результаты соответствовали действительности;

2) развитие ораторского искусства и искусства спора. Основателем логики как науки принято считать Аристотеля. Однако первое систематическое изложение логических проблем было раньше дано другим древнегреческим философом – Демокритом. Среди его многочисленных трудов был и обширный трактат в трех книгах «О логическом, или о канонах» (от греч. canon – «правило, предписание»). В данной работе была раскрыта сущность основных форм познания и критерии истины, показана роль логических рассуждений в познании, дана классификация суждений и предпринята попытка разработать индуктивную логику. В центре логических размышлений Аристотеля лежит теория дедуктивных умозаключений и доказательства. Он также дал классификацию категорий и близкую к демокритовской классификацию суждений, сформулировал три фундаментальных закона мышления – закон тождества, закон противоречия и закон исключенного третьего.

В Средние века в развитии логики как науки сыграла проблема общих понятий – «универсалий». Суть проблемы заключается в том, что появляется раньше – общие понятия, вытекающие из нашего разума (рационализм), или единичные, фактические предметы (номинализм).

В эпоху Возрождения логика переживала настоящий кризис. Она расценивалась как искусственное мышление и противопоставлялась естественному мышлению, основывающемуся на интуиции и воображении.

Следующий этап в развитии логики начинается с XVII в. Он связан с созданием в ее рамках индуктивной логики, в которой нашли отражение многообразные процессы получения общих знаний на основе накопившегося эмпирического материала. Потребность в таких знаниях наиболее полно осознал и выразил в своих трудах Ф. Бэкон. Он и стал родоначальником интуитивной логики. Растущие потребности научно-технического прогресса обусловливают дальнейшее развитие современной логики.