Основные функции алгебры логики
Лекция 4.
Функции алгебры логики одной переменной.
Количество ФАЛ одной переменной х равно 4. Представим обобщенную таблицу истинности для каждой из четырех функций в виде табл. 2.
Таблица 2
| х | f0(x) | f1(x) | f2(x) | f3(x) |
Функция f0(x) независимо от значения переменной х принимает нулевой значение и поэтому называется функцией тождественно равной 0: f0(x) = 0.
Функция f3(x) независимо от значения переменной х принимает единичное значение и поэтому называется функцией тождественно равной 1: f3(x) = 1.
Значения функции f1(x) совпадают со значением входной переменной х, поэтому эта функция называется функцией повторения: f1(x) = х.
Значения функции f2(x) противоположны значениям переменной х, поэтому эта функция называется инверсной функцией или функцией отрицания: f1(x) = 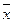 .
.
Рассмотрим примеры реализации этих функций на логических элементах, принимая во внимание, что в большинстве случаев сигналу лог.0 соответствует низкий потенциал, а сигналу лог. 1 – высокий потенциал.
На рис. 17, а представлен вариант реализации функций тождественно равных 0 и 1 за счет подключения выходных шин непосредственно к источникам высокого (+U) и низкого потенциала (общий провод). На рис. 17, б представлен вариант реализации функции повторения f1(x) за счет подключения выходной шины непосредственно к источнику входного сигнала х и функции отрицания f2(x) за счет подачи входного сигнала х на логический элемент НЕ, реализующий функцию инверсии входного сигнала. В качестве элемента НЕ может быть использован транзистор, включенный по схеме с общим эмиттером (см. рис. 11, а).

Рис. 17
При использовании электромагнитных реле функция f0(x) формируется разрывом электрической цепи, рис. 18, а. Функция f3(x) формируется за счет короткого замыкания фронтового контакта реле в электрической цепи, рис. 18, б. Функция f1(x) может быть реализована использованием в электрической цепи фронтового контакта у реле Y, на обмотку которого подается входной сигнал х, рис. 18, в. Функция f2(x) реализуется посредством включения в электрическую цепь тылового контакта 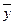 реле Y, на обмотку которого подается входной сигнал х, рис. 18, г.
реле Y, на обмотку которого подается входной сигнал х, рис. 18, г.
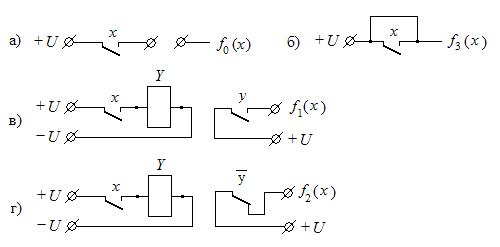
Рис. 18
Функции алгебры логики двух переменных.
Количество различных наборов значений двух переменных равно 4, следовательно, количество разных ФАЛ, которые можно реализовать на этих наборах, равно 24 = 16.
Представим обобщенную таблицу истинности для каждой из шестнадцати функций в виде табл. 3.
Таблица 3
| х2 | х1 | Обозначение функций | |||||||||||||||
| & | ∆ | х2 | ∆ | х1 |  | v | ↓ | ~ |  | → | 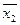 | → | ׀ | ||||
| f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | ||
В число шестнадцати ФАЛ входят функции тождественно равные 0 и 1; функции повторения значений входных переменных х1 и х2; функции – инверсии значений входных переменных:
f0(x) = 0; f3(x) = х2; f5(x) = х1; f10(x) =  ; f12(x) =
; f12(x) = 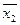 ; f15(x) = 1.
; f15(x) = 1.
Функция f1(x) соответствует логической операции И, называемой часто конъюнкцией или логическим умножением. Функция принимает единичное значение тогда, когда обе переменные равны 1.
Пример равносильных вариантов аналитической записи функции f1(x):
f1(x) = х2∙х1 = х2∩х1 = х2&x1.
Пример технической реализации функции f1(x) на контактах электромагнитных реле. 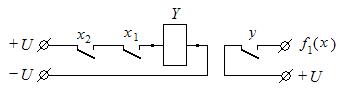
Функция f2(x) соответствует логической операции запрета. Функция повторяет значение входного сигнала х2 тогда, когда х1 = 0 (снятие запрета со стороны переменной х1 на пропуск через ключ единичного значения входного сигнала х2).
Пример равносильных вариантов аналитической записи функции f2(x):
f2(x) = х2∆х1 = х2∙  = х2∩
= х2∩  = х2&
= х2&  .
.
Функция f4(x) также соответствует логической операции запрета. Однако данная функция повторяет уже значение входного сигнала х1 тогда, когда х2 = 0 (снятие запрета со стороны переменной х2 на пропуск через ключ единичного значения входного сигнала х1).
Пример равносильных вариантов аналитической записи функции f4(x):
f4(x) = х1∆х2 = 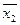 ∙х1 =
∙х1 = 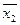 ∩х1 =
∩х1 = 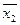 &х1.
&х1.
Пример технической реализации функций f2(x) и f4(x) на контактах электромагнитных реле. 
Функция f6(x) соответствует логической операции «сложение по модулю 2». Это наиболее употребительная логическая операция, применяемая в таких дискретных устройствах, как сумматоры, осуществляющие операции сложения двоичных чисел, и кодеры или декодеры, осуществляющие кодирование или декодирование информации. Функция f6(x) принимает единичное значение при условии неравенства значений переменных х1 и х2.
Пример равносильных вариантов аналитической записи функции f6(x):
f6(x) = х2 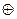 х1 = х2∙
х1 = х2∙ 

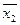 ∙х1 = х2∙
∙х1 = х2∙  +
+ 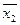 ∙х1.
∙х1.
В приведенном выражении знаки  и + есть условные обозначения логической операции сложения.
и + есть условные обозначения логической операции сложения.
Пример технической реализации функции f6(x) на контактах электромагнитных реле. 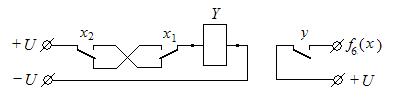
Функция f7(x) соответствует логической операции ИЛИ, называемой часто дизъюнкцией или логическим сложением. Функция принимает единичное значение тогда, когда хотя бы одна из переменных равна 1.
Пример равносильных вариантов аналитической записи функции f7(x):
f7(x) = х2 + х1 = х2  х1 = х2∙
х1 = х2∙  +
+ 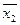 ∙х1 + х2∙х1.
∙х1 + х2∙х1.
Пример технической реализации функции f7(x) на контактах
электромагнитных реле. 
Функция f8(x) соответствует логической операции «отрицание ИЛИ», называемой функцией (ИЛИ НЕ) или функцией «стрелка Пирса». Данная функция принимает единичное значение тогда, когда обе переменные принимают нулевое значение.
Пример равносильных вариантов аналитической записи функции f8(x):
f8(x) =  =
=  = х2 ↓ х1.
= х2 ↓ х1.
Пример технической реализации функции f8(x) на контактах электромагнитных реле. 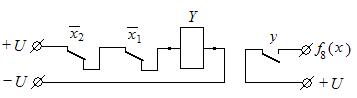
Функция f9(x) соответствует логической операции «эквивалентность». Данная функция принимает единичное значение при условии, что значения обеих переменных имеют одинаковые значения. Функция эквивалентности может применяться в дискретных устройствах, выполняющих функцию сравнения двоичных чисел. Функция f9(x) является инверсной по отношению к функции f6(x) «сложение по модулю 2».
Пример равносильных вариантов аналитической записи функции f9(x):
f9(x) = 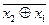 =
=  + х2∙х1 = (х2 +
+ х2∙х1 = (х2 +  ) ∙ (
) ∙ ( 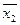 + х1).
+ х1).
Пример технической реализации функции f9(x) на контактах электромагнитных реле. 
Функции f11(x) и f13(x) соответствуют логической операции «импликация». Функция f11(x) принимает единичное значение во всех случаях, кроме одного, когда х2 = 0, а х1 = 1. Таким образом, функция f11(x) при х1 = 1 повторяет значение входного сигнала х2, а при х1 = 0 – функция становится тождественно равной 1.
Функция f13(x) принимает единичное значение во всех случаях, кроме одного, когда х2 = 1, а х1 = 0. Таким образом, функция f13(x) при х2 = 1 повторяет значение входного сигнала х1, а при х2 = 0 – функция становится тождественно равной 1.
Пример равносильных вариантов аналитической записи функций f11(x) и f13(x):
f11(x) = х1 → х2 = х2 +  ;
;
f13(x) = х2 → х1 = 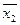 + х1.
+ х1.
Пример технической реализации функций f11(x) и f13(x) на контактах электромагнитных реле. 
Функция f14(x) соответствует логической операции «отрицание И», называемой функцией (И НЕ) или функцией «штрих Шеффера». Данная функция принимает нулевое значение тогда, когда обе переменные принимают единичное значение.
Пример равносильных вариантов аналитической записи функции f14(x):
f14(x) =  =
=  = х2 │ х1.
= х2 │ х1.
Пример технической реализации функции f14(x) на контактах электромагнитных реле. 
На этапе структурного синтеза дискретных устройств автоматики и телемеханики используются следующие условные обозначения логических элементов, реализующих некоторые элементарные функции алгебры логики от двух переменных, рис. 19.

Рис. 19
Задачи для самостоятельного решения
1. Сколько функций алгебры логики можно реализовать на наборах из трех и четырех переменных. Ответ: 256 и 65536.
2. Дискретное устройство реализует следующую ФАЛ:
у = х1∙х2∙(х3 + х4) + 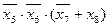 .
.
Определить сколько и каких логических элементов, имеющих два входа, потребуется для построения дискретного устройства.
Ответ: 7 (3 элемента И, 2 элемента ИЛИ, 1 элемент ИЛИ-НЕ и 1 элемент – импликатор).
3. Построить структурную схему дискретного устройства из задачи 2, используя 7 логических элементов на два входа. Ответ:
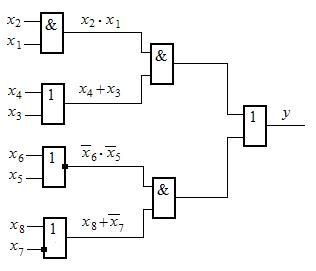
4. Ниже на рисунке представлена структурная схема некоторого дискретного устройства, составлена из элементарных логических элементов на два входа. Составить аналитическое выражение для ФАЛ, реализуемой данным дискретным устройством, и дать пояснение к этой функции.

Ответ: у = х2∙  +
+ 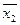 ∙х1. Реализуемая дискретным устройством ФАЛ – есть логическая операция «сложение по модулю 2».
∙х1. Реализуемая дискретным устройством ФАЛ – есть логическая операция «сложение по модулю 2».
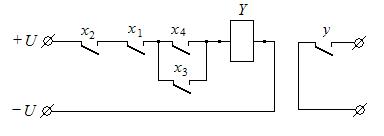
5. Построить релейно-контактную схему, реализующую следующую ФАЛ:
у = х1∙х2∙(х3 + х4)
Ответ:
6. Ниже на рисунке представлена релейно-контактная схема, реализующая некоторую логическую функцию у.

Составить аналитическое выражение для логической функции у, реализуемой фронтовым контактом реле Y. Ответ: у = 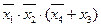 .
.
