Отношения между суждениями

Отношения между простыми суждениями

1. Несравнимые суждения имеют различные субъекты и предикаты.

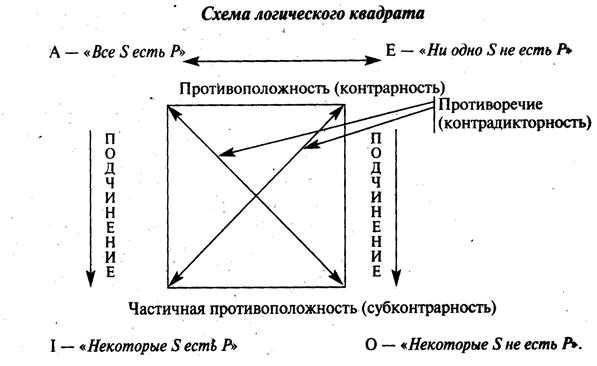
2. Сравнимые сужденияимеют один и тот же субъект и предикат. Их называют суждениями одинаковой материи. Они могут различаться между собой кванторами и связками. Между суждениями этого рода устанавливаются определенные твердые соотношения по их истинностным значениям, которые удобно изображать графически с помощью логического квадрата. Буквы на его углах символизируют различные виды суждений - A, E, I, O. А его стороны и диагонали выражают всю совокупность возможных отношений между ними.

Сравнимые суждения разделяются на совместимые и несовместимые.

К совместимым относятся суждения, которые одновременно могут быть истинными. Различают три вида совместимости:

- эквивалентность (полная совместимость). Эквивалентными являются такие суждения, которые имеют одинаковые логические характеристики: одинаковые субъекты и предикаты, однотипную — утвердительную или отрицательную — связку, одну и ту же выраженную квантором количественную характеристику. С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются. Эти суждения принимают одни и те же значения истинности.

- частичная совместимость (субконтрарность). Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

- подчинение. Подчинение имеет место между суждениями А и I, E и О. Для них характерны следующие две зависимости: при истинности общего суждения частное всегда будет истинным, и, при ложности частного суждения общее суждение также будет ложным.

Несовместимыми являются суждения, которые одновременно не могут быть истинными. Различают два вида несовместимости:

- противоположность (контрарность). Противоположными являются суждения А и Е, которые одновременно не могут быть истинными, но могут быть одновременно ложными.

- противоречие (контрадикторность). Противоречащими являются суждения А и О, Е и I, которые одновременно не могут быть ни истинными, ни ложными.

Отношения между сложными суждениями

Сложные суждения также могут быть сравнимыми и несравнимыми.

1. Несравнимые — это суждения, которые не имеют общих пропозиционных переменных.

2. Сравнимые — это суждения, которые имеют одинаковые пропозиционные переменные (составляющие) и различаются логическими связками, включая отрицание.

Сложные сравнимые суждения могут быть совместимыми и не совместимыми.

2.1. Совместимые суждения могут быть одновременно истинными. Как и в случае простых суждений, различают три вида совместимости сложных суждений:

- эквивалентность. Эквивалентные— это суждения, которые принимают одни и те значения истинности. Существует четыре основные эквивалентности:

1) выражение конъюнкции через дизъюнкцию

ù(A^B) = ùA v ùB

2) выражение дизъюнкции через конъюнкцию

ù (A v B) = ùA ^ ùB

3) выражение импликации через конъюнкцию

A ® B =ù (A ^ ùB)

4) выражение импликации через дизъюнкцию

A ® B = ù A v B

- частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

- подчинение. Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующего все виды рассуждений.

2.2.Несовместимыми являются суждения, которые одновременно не могут быть истинными.

- противоположность — отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.

- противоречие — отношение между суждениями, которые одновременно не могут быть ни истинными, ни ложными. Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию.

Логическое исчисление как тип формальной теории^٭

Понятие содержательной и формальной теории: в содержательных теориях исходные утверждения (посылки) рассуждения представляют собой некоторые допущения, а дедукция используется лишь для связи некоторых отдельных положений теории. Заключение при этом интерпретируется как условно истинное, т. е. зависит от истинности посылок (школьная арифметика, теория эволюции Дарвина, а также сама логика высказываний и логика предикатов). В формальных теори оформляется (структурируется) не только само знание, но и средства его получения – логические законы и способы дедуктивного рассуждения.

Исчисление: формальная теория, в которой содержание фиксируется на специально созданном символическом языке, а все рассуждения в рамках этой теории строятся как преобразования одних последовательностей символов в другие их последовательности (формальные теории множеств, формальная арифметика, логическое исчисление).

Формальное рассуждение – выведение одних формул из других формул. ФР можно трактовать как модель (форму) различных содержательных рассуждений, имеющих ту же самую логическую структуру, т.е. формулы исчислений представляют собой логические формы высказываний.

Натуральное логическое исчисление: содержит только правило вывода и не содержит аксиом.

Если в содержательных логических теориях под логическим законом понимается общезначимая формула (формула принимающая значение «истина» при любых интерпретациях нелогических символов), а критерием правильности умозаключения является наличие семантического отношения логического следования между его посылками и заключением, то в логических исчислениях осуществляется попытка формализации данных понятий. С это целью здесь вводятся синтаксические аналоги понятия общезначимой формулы и отношения логического следования – понятия теоремы (синтаксический аналог «общезначимой формулы» - и отношение выводимости (синтаксический аналог «отношения логического следования» - из множества формул (посылок) логически следует другая формула (заключение) тогда и только тогда, когда при любой интерпретации параметров в составе посылок и заключения, при которой все выражения из посылок принимают значение «истина», выражение заключения также примет значение «истина».

Правила вывода натурального исчисления^٭

Правила вывода:

1) &_{в (введение конъюнкции)} 5) &_{и (исключение конъюнкции)}

А , В А & ВА & В

А & В А В

2) v_{в (введение дизъюнкции)} 6) v_{и (исключение дизъюнкции - tollendo ponens)}

А__ _А__ А v В, А_

А v В А v В В

3) →_{в (введение импликации)} 7) →_{и (исключение импликации - modus ponens)}

__В___ А → В, А

С → В , где С- посл. пос. В

4) _{В (введение отрицания)} 8) _{и (введение отрицания)}

В, ВА