Построение функций принадлежности

Рецензия

Оглавление

Рецензия. 1

Лист задания. 3

Введение. 4

1. Построение нечёткого дерева решений. 6

1.1 Определение лингвистических переменных. 6

1.2 Построение функций принадлежности. 7

1.3 Расчёт E(S^N), G(S^N) 8

1.4 Расчёт степеней принадлежности к каждому новому узлу. 11

1.5 Расчёт принадлежности новой записи к целевому классу. 14

2. Построение нечёткой экспертной системы в программном пакете CubiCalc 2.0. 16

2.1 Определение переменных Fuzzy Input, Output 16

2.2 Построение функций принадлежности. 17

2.3 Определение набора правил, связывающих входные переменные с выходными. 19

2.4 Настройка входного файла. 20

2.5 Проверка работы системы.. 20

Заключение. 21

Список использованных источников. 22

Лист задания

Вариант 9

Магазин спортивных товаров. Руководству компании необходимо определить место организации магазина представленного направления.

Введение

Проблемы принятия решений в сложных условиях занимают в настоящее время особое место в информационных технологиях. Математические методы широко применяются для описания и анализа сложных экономических, социальных и других систем. Теория оптимизации создала совокупность методов, помогающих при использовании ЭВМ эффективно принимать решения при известных и фиксированных параметрах или когда параметры - случайные величины с известными законами распределения. Существует, однако, ряд задач, которые не поддаются формальному описанию в силу того, что часть параметров представляют собой неточно или качественно заданные величины, для которых переход от «принадлежности к классу» к «непринадлежности» непрерывен. Традиционные методы недостаточно пригодны для решения подобных задач именно потому, что они не в состоянии описать возникающую неопределенность.

В основе нечеткой логики лежит теория нечетких множеств, где функция принадлежности элемента множеству не бинарна (да/нет), а может принимать любое значение в диапазоне 0-1. Это дает возможность определять понятия, нечеткие по самой своей природе: "хороший", "высокий", "слабый" и т.д. Нечеткая логика дает возможность строить базы знаний и экспертные системы нового поколения, способные хранить и обрабатывать неточную информацию. Системы, основанные на нечеткой логике, разработаны и успешно внедрены в таких областях, как управление технологическими процессами, управление транспортом, управление бытовой техникой, медицинская и техническая диагностика, финансовый менеджмент, финансовый анализ, биржевое прогнозирование, распознавание образов, исследование рисковых и критических операций, прогнозирование землетрясений, составление автобусных расписаний, климатический контроль в зданиях.

Цель курсовой работы: изучить нечеткую логику в системе моделирования.

Для достижения данной цели поставлены следующие задачи:

• 
  изучить литературу по данной теме;
• 
  определить лингвистические переменные;
• 
  построить нечёткое дерево решений;
• 
  построить функции принадлежности;
• 
  рассмотреть алгоритм нечеткого вывода;
• 
  изучить процесс моделирования;
• 
  определить место организации магазина.

Построение нечёткого дерева решений

В данном разделе необходимо построить нечеткое дерево решений, с помощью которого определить рейтинг выбора места организации магазина, который посещают 50 000 тысяч человек за месяц и расстояние до базы 40 км.

В таблице 1 представлены данные о семи местах организации магазина: проходимость (определена, исходя из оценок, выставляемых рейтинговым агентством), расстояние до базы (в километрах) и рейтинг (определен экспертом).

Табл. 1 - данные о месте организации магазина

№	Проходимость	Расстояние	Рейтинг
D1	10.000		0,0
D2	15.000		0,0
D3	25.000		0,3
D4	30.000		0,4
D5	35.000		0,5
D6	40.000		0,8
D7	55.000

Определение лингвистических переменных

1) х₁: «проходимость»;

Х: [0;60.000];

Т(х): «низкая», «средняя», «большая»;

G: «достаточно», «недостаточно»;

М: задано таблично (таблица 2).

2) х₂: «расстояние»;

Х: [0, 50];

Т(х): «малое», «среднее», «большое»;

G: «достаточно», «недостаточно»;

М: задано таблично (таблица 3).

Табл.2 - Табличное представление семантического правила для х₁

№	Проходимость
низкая	средняя	большая
D1	1,0	0,0	0,0
D2	0,8	0,2	0,0
D3	0,5	0,5	0,0
D4	0,2	0,8	0,0
D5	0,0	0,5	0,5
D6	0,0	0,0	1,0
D7	0,0	0,0	1,0

№	Расстояние
маленькое	среднее	большое
D1	1,0	0,0	0,0
D2	0,4	0,6	0,0
D3	0,0	1,0	0,0
D4	0,0	0,8	0,2
D5	0,0	0,0	1,0
D6	0,0	0,1	0,9
D7	0,0	0,2	0,8

Построение функций принадлежности

Общий вид функций принадлежности лингвистических переменных показан на рисунке 1.

1

0 Проходимость

1

0 Расстояние

Рис.1 - Графики функции принадлежности

1.3 Расчёт E(S^N), G(S^N)

Необходимо найти значение общей энтропии:

Р_да = 0+0+0,3+0,4+0,5+0,8+1,0= 3

Р_нет =1,0+1,0+ 0,7+0,6+0,5+0,2+0=4

Р= Р_да +Р_нет =7

Рассчитываем значение энтропии E(S^N), воспользовавшись формулой :

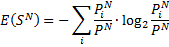
E(S^N)= -3/7*log₂3/7 – 4/7*log₂4/7 » 0,985 бит

Рассчитаем E(S^N, проходимость).

E(S^N, проходимость, низкая):

Р_да^низкая=min(0;1)+min(0;0,8)+min(0,3;0,5)+min(0,4;0,2)+min(0,5;0)+min(0,8;0)+min(1;0)=0+0+0,3+0,2+0+0+0=0,5

Р_нет^низкая=min(1;1)+min(1;0,8)+min(0,7;0,5)+min(0,6;0,2)+min(0,5;0)+min(0,2;0)+ min (0;0)=1+0,8+0,5+0,2+0+0+0=2,5

Р^низкая= Р_да +Р_нет =0,5+2,5=3,0

E(проходимость, низкая)= - 0,5/3,0* log₂0,5/3,0-2,5/3,0* log₂2,5/3,0=0,65 бит

Рассчитаем E(S^N, проходимость, средняя).

Р_да^{средняя}=min(0;0)+min(0;0,2)+min(0,3;0,5)+min(0,4;0,8)+min(0,5;0,5)+min(0,8;0)+min(1;0)=0,3+0,4+0,5=1,2

Р_нет^{средняя}= min(1;0)+min(1;0,2)+min(0,7;0,5)+min(0,6;0,8)+min(0,5;0,5)+min(0,2;0)+min(0;0)=0,2+0,5+0,6+0,5=1,8

Р^{средняя}= 1,2+1,8=3

E(проходимость, средняя)= - 1,2/3* log₂1,2/3-1,8/3* log₂1,8/3=0,97 бит

Рассчитаем E(S^N, проходимость, большая).

Р_да^{большая}=min(0;0)+min(0;0)+min(0,3;0)+min(0,4;0)+min(0,5;0,5)+min(0,8;1)+min(1;1)=0,5+0,8+1=2,3

Р_нет^{большая}=min(1;0)+min(1;0)+min(0,7;0)+min(0,6;0)+min(0,5;0,5)+min(0,2;1)+min(0;1)=0,5+0,2=0,7

Р^{большая}= 2,3+0,7=3

E(проходимость, большая)= - 2,3/3* log₂2,3 /3-0,7/3* log₂0,7/3=0,78 бит

Табл. 4 - итоги расчетов для х₁

	низкая	средняя	большая
Рда	0,5	1,2	2,3
Рнет	2,5	1,8	0,7
E, бит	0,65	0,97	0,78

Найдём энтропию, воспользовавшись формулой:

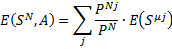
E(S^N ,проходимость)= - 2,5/7* 0,65+1,8 /7*0,97+ 0,7/7* 0,78=0,56 бит

Рассчитаем прирост информации для данного атрибута.

G(S^N,проходимость)= 0,98-0,56= 0,42 бит

Рассчитаем E(S^N, расстояние).

E(S^N, расстояние, маленькое):

Р_да^{маленькое}=min(0;1)+min(0;0,4)+min(0,3;0)+min(0,4;0)+min(0,5;0)+min(0,8;0)+min(1;0)=0

Р_нет^{маленькое} =min(1;1)+min(1;0,4)+min(0,7;0)+min(0,6;0)+min(0,5;0)+min(0,2;0)+ min(0;0)=1+0,4=1,4

Р^{маленькое}= Р_да +Р_нет =0+1,4=1,4

E(расстояние,маленькое)= - 0/1,4* log₂0/1,4-1,4/1,4* log₂1,4/1,4=0 бит

E(S^N, расстояние,среднее):

Р_да^{среднее}=min(0;0)+min(0;0,6)+min(0,3;1)+min(0,4;0,8)+min(0,5;0)+min(0,8;0,1)+min(1;0,2)=1

Р_нет^{среднее}=min(1;0)+min(1;0,6)+min(0,7;1)+min(0,6;0,8)+min(0,5;0)+min(0,8;0,1)+ min(1;0,2)=0,6+0,7+0,6+0,1+0,2=2,2

Р^{среднее}= Р_да +Р_нет =1+2,2=3,2

E(расстояние,среднее)= - 1/3,2* log₂1/3,2-2,2/3,2* log₂2,2/3,2=0,896 бит

E(S^N, расстояние,большое):

Р_да^{большое}=min(0;0)+min(0;0)+min(0,3;0)+min(0,4;0,2)+min(0,5;1)+min(0,8;0,9)+min(1;0,8)=0,2+0,5+0,8=0,8=2,3

Р_нет^{большое}=min(1;0)+min(1;0)+min(0,7;0)+min(0,6;0,2)+min(0,5;1)+min(0,2;0,9)+ min(0;0,8)=0,2+0,5+0,2=0,9

Р^{большое}= Р_да +Р_нет =2,3+0,9=3,2

E(расстояние,большое)= - 2,3/3,2* log₂2,3/3,2-0,9/3,2* log₂0,9/3,2=0,857 бит

Табл. 5 - итоги расчетов для х₂

	маленькое	среднее	большое
Рда			2,3
Рнет	1,4	2,2	0,9
E, бит		0,896	0,857

E(S^N, расстояние)= 1,4/7*0+2,2/7*0,896+0,9/7*0,857=0,391 бит

G(S^N,расстояние)= 0,985-0,391= 0,594 бит

Максимальны прирост информации обеспечивает атрибут «расстояние», следовательно, разбиение начнется с него.