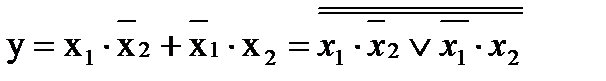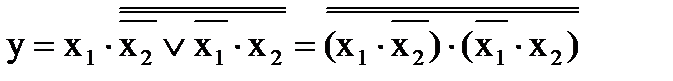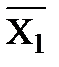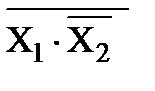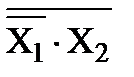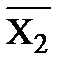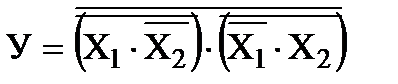Тема : Синтез КЦП. Таблиця істинності. Форми запису логічних функцій. Побудова логічних схем у базисах І-АБО-НЕ, І-НЕ, АБО –НЕ
Цель:Изучить основные способы записи логических выражений. Ознакомиться с основными принципами построения КЦУ.
План:
1. Синтез комбинационных цифровых устройств.
2. Таблица истинности КЦУ. Формы записи логических функций
3. Построение логических схем в базисах И, ИЛИ,НЕ, И-НЕ, ИЛИ-НЕ
Ход лекции
1)ЦУ начинают создавать с определения логической функции, которая описывает принцип действия схемы. Эту задачу называют логическимсинтезом.
Синтез комбинационных логических схем содержит 4 этапа:
1. Составляется таблица функционирования логической цепи – таблица истинности. Эта таблица показывает, чему равен выходной сигнал цепи при различных сочетаниях входных сигналов.
2. Запись логической функции по таблице истинности в совершенной дизъюнктивной нормальной форме (СДНФ) или в совершенной конъюнктивной нормальной форме (СКНФ).
3. Минимизация логической функции с помощью карт Карно для получения минимальных форм функции, которые при реализации дают возможность использовать минимальное количество логических элементов заданного типа.
4. Построение логической схемы по полученной минимальной форме логической функции.
2)При табличном способе задания логическая функция представляется в виде таблицы, в которой записываются все возможные наборы значений аргументов и соответствующее каждому набору аргументов значение логической функции 0 или 1. Наборы аргументов в таблице записывают в порядке возрастания.
Пример 1:
Выполним п.1, составим таблицу функционирования логической цепи, например, для построения ячейки «голосования» на три входа, т.е. такую ячейку, у которой сигнал на выходе равен единице тогда, когда большинство входных сигналов равно единице.
Существуют две формы записи логической функции в аналитическом виде – СДНФ и СКНФ.
Форму записи логической функции называют нормальной, если в каждый член логической суммы (произведения) аргумент или его инверсия входит не более одного раза.
Если каждый член логического выражения содержит все аргументы или их инверсии, то такую форму записи называют совершенной.
Для создания логического уравнения в СДНФ необходимо выполнить следующие действия:
1) выбрать из таблицы истинности наборы аргументов, на которых функция принимает значение 1;
2) записать формулу логического произведения всех аргументов столько раз, сколько функция принимает значение 1; все записанные произведения соединить знаками логической суммы;
3) если аргумент в наборе равен 1, он записывается без инверсии, если аргумент равен 0 – с инверсией.
Пример для СДНФ:
1)
| Аргументы | Функция | | х1 | х2 | y | | | | | | | | | | | | | | | | | |
выбрали 2 набора, когда y=1
2) х1·х2Vх1·х2
3) в первом наборе х1=0, следовательно, над х1 ставим знак инверсии; во втором наборе х2=0, следовательно, над х2 ставим знак инверсии.
СДНФ: 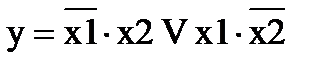
Для Примера 1 получим:
F = 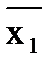 x2x3 + x1
x2x3 + x1 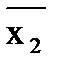 x3 + x1x2
x3 + x1x2 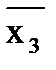 + x1x2x3
+ x1x2x3
Чтобы составить логическое уравнение в СКНФ, необходимо выполнить следующие действия:
1) выбрать из таблицы истинности наборы аргументов, на которых функция принимает значение 0;
2) записать формулу логической суммы всех аргументов столько раз, сколько функция принимает значение 0; все записанные суммы соединить знаками логического произведения;
3) если аргумент в наборе равен 1, он записывается с инверсией, если аргумент равен 0 – без инверсии.
| Аргументы | Функция | | х1 | х2 | y | | | | | | | | | | | | | | | | | |
Пример для СКНФ:
1) выбираем 2 набора, когда y = 0
2) (x1Vx2)·(x1Vx2)
3) в первом наборе нет единичных значений аргументов, следовательно, первая сумма остается без изменений, во втором наборе оба аргумента = 1, следовательно, над ними ставим знак инверсии.
СКНФ: y = (x1Vx2)·( 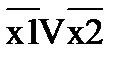 )
)
Для Примера 1 получим:
F = (x1Vx2Vx3) (x1Vx2V 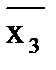 ) (x1V
) (x1V 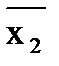 Vx3) (
Vx3) ( 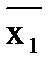 Vx2Vx3)
Vx2Vx3)
Если по СКНФ или СДНФ логической функции построить логическую схему, то, очевидно, что такая схема будет выполнять заданный закон функционирования, но будет содержать большое число ЛЭ, что является неэкономичным и снижает надежность устройства. Поэтому построению логической схемы должна предшествовать операция получения самой короткой формы записи логической функции – минимизация.
3)Любое ЦУ можно построить из комплектов трех логических элементов: И, ИЛИ, НЕ. При этом количество всех переменных с инверсиями в синтезированном логическом уравнении определяет количество необходимых элементов НЕ, количество всех логических произведений – количество элементов И, а количество всех логических сумм равно количеству необходимых элементов ИЛИ.
Пример1: в результате логического синтеза получили:
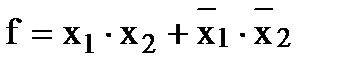
Уравнение имеет 2 знака инверсии, 2 знака логического умножения и 1 знак логической суммы. Т.о., чтобы построить схему, необходимо иметь:
–
| приоритет выполнения операций |
два элемента НЕ
– два элемента И
– один элемент ИЛИ
Пример 2: 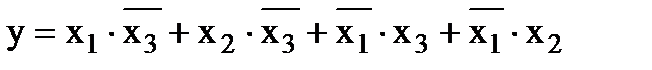 (кодовый замок)
(кодовый замок)
Для построения принципиальной схемы, реализующей уравнение необходимо иметь:
– 2 логических элемента НЕ 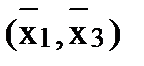
– 4 логических элемента И 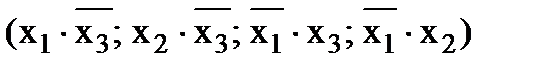
– 3 логических элемента ИЛИ (вместо 3-х ИЛИ на 2 входа можно использовать один четырехвходовой).
Пример 3: у = х1 · х2 v x2 · x3 v x1 · x3
| Необходимо: – 3 элемента И; – 2 элемента ИЛИ (вместо 2 ИЛИ можно использовать один трехвходовй) |
Построение КЦУ в базисе И-НЕ
Промышленные ИМС какого-либо назначения строят на базе логических элементов И-НЕ или ИЛИ-НЕ.
При построении схем на элементах И-НЕ логические уравнения преобразовывают так, чтобы у них не было знаков сложения. Этого достигают, используя законы де Моргана.
Пример 1. Построить схему устройства на элементах И-НЕ, которая реализует функцию сложения двух аргументов.
Выходное уравнение: у = х1 v х2. Преобразуем его так, чтобы в нем не было знака логического сложения. Для этого сначала поставим над логическим уравнением 2 знака инверсии: 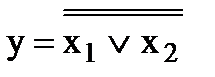 (значение у при этом не изменится). Далее выражение под верхним знаком инверсии преобразовываем по закону де Моргана:
(значение у при этом не изменится). Далее выражение под верхним знаком инверсии преобразовываем по закону де Моргана: 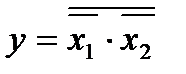 .
.
Построим схему по данному выражению.
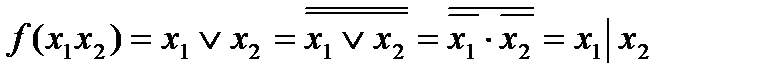
Пример 2. Построить схему логического уравнения, которое реализует функцию И на элементах И-НЕ.
у = х1·х2
Т.к. в этом выражении нет знаков логического сложения, то, чтобы построить схему, достаточно над правой частью уравнения поставить знак двойной инверсии (закон двойного отрицания):
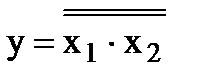
Пример 3. Построить схему инвертора на логических элементах И-НЕ.
Логическое уравнение инвертора у =
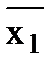
. Это уравнение можно получить из уравнения элемента И-НЕ у =
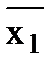
·
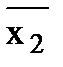
, если объединить его входы. Пусть х
1 = х
2, тогда из уравнения элемента И-НЕ вытекает:
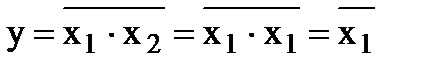
Пример 4. Построить схему, которая реализует логическое уравнение:
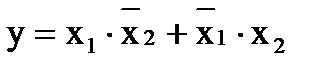 на элементах И-НЕ
на элементах И-НЕ
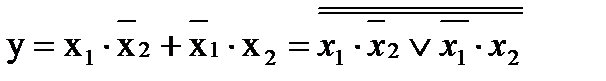
Т.к. в уравнении есть знак логического сложения, то преобразуем выражение под верхним знаком инверсии по правилу де Моргана:
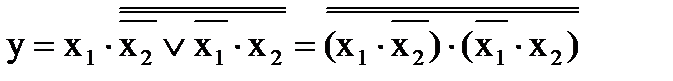
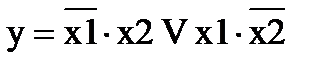
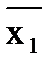 x2x3 + x1
x2x3 + x1 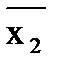 x3 + x1x2
x3 + x1x2 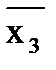 + x1x2x3
+ x1x2x3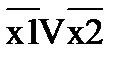 )
)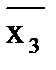 ) (x1V
) (x1V 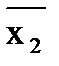 Vx3) (
Vx3) ( 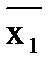 Vx2Vx3)
Vx2Vx3)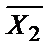
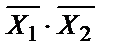
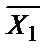
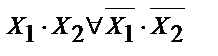
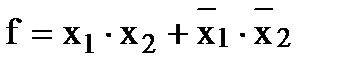
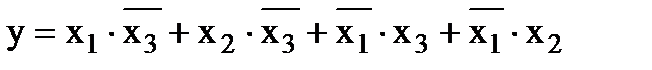 (кодовый замок)
(кодовый замок)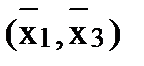
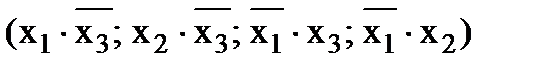
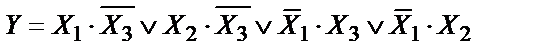
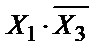
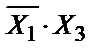
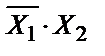
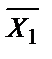
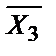
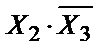
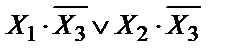
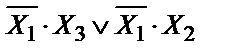
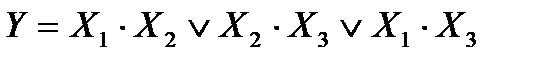
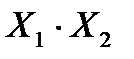
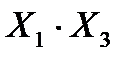
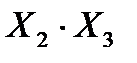
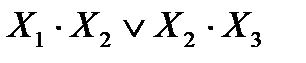
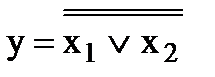 (значение у при этом не изменится). Далее выражение под верхним знаком инверсии преобразовываем по закону де Моргана:
(значение у при этом не изменится). Далее выражение под верхним знаком инверсии преобразовываем по закону де Моргана: 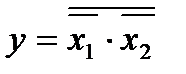 .
.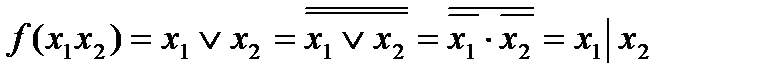
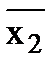
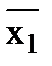
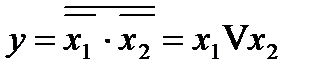
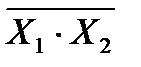
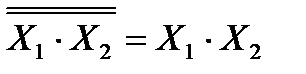
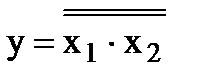
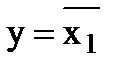
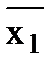 . Это уравнение можно получить из уравнения элемента И-НЕ у =
. Это уравнение можно получить из уравнения элемента И-НЕ у = 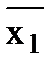 ·
· 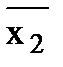 , если объединить его входы. Пусть х1 = х2, тогда из уравнения элемента И-НЕ вытекает:
, если объединить его входы. Пусть х1 = х2, тогда из уравнения элемента И-НЕ вытекает: 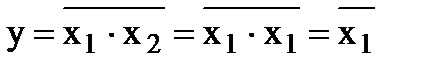
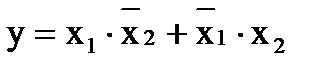 на элементах И-НЕ
на элементах И-НЕ