Етоды анализа и синтеза комбинационных схем.

Техническим аналогом булевой функции в вычислительной технике является комбинационная схема, на вход которой поступают и с выхода снимаются электрические сигналы в виде одного из уровней напряжения, соответствующих значениям логического 0 и логической 1.

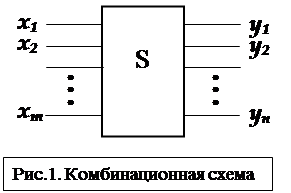Рассмотрим схему S, имеющую m входов и n выходов (рис. 1). На её входы могут быть поданы наборы значений входных переменных x_i {0,1}, 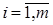, а на выходах формируются выходные переменные y_jÎ{0,1}, .

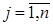Схема S называется комбинационной, если каждую из n функций её выходов y_1, y_2,…, y_n можно представить как булеву функцию входных переменных x_1, x_2,…,x_m.

Комбинационная схема описывается с помощью системы уравнений (1), где F_i– булева функция.

y₁ = F₁(x_1, x_2,…,x_m)

(1)

y₂ = F₂(x_1, x_2,…,x_m)

_{. . . . . . . . . . . . . . . . . . . . . . . .}

y_n = F_n(x_1, x_2,…,x_m)

Как следует из определения комбинационной схемы, значения выходных переменных y_jв произвольный момент времени однозначно определяются значениями входных переменных x_i.

Структурно комбинационная схема может быть представлена как совокупность элементарных логических схем – логических элементов (ЛЭ). ЛЭ выполняют над входными переменными элементарные логические операции типа И-НЕ, И, ИЛИ, ИЛИ-НЕ и т.д. Число входов логического элемента соответствует числу аргументов воспроизводимой им булевой функции. Графическое изображение комбинационной схемы, при котором показаны связи между различными элементами, а сами элементы представлены условными графическими обозначениями (УГО), называется функциональной схемой.

В ходе разработки комбинационных схем приходится решать задачи анализа и синтеза.

Задача анализа состоит в определении статических и динамических свойств комбинационной схемы. В статике определяются булевы функции, реализуемые комбинационной схемой, по известной ее структуре. В динамике рассматривается способность надёжного функционирования схемы в переходных процессах при смене значений переменных на входах схемы, т.е. определяется наличие на выходах схемы возможных нежелательных импульсных сигналов («просечек»), которые не следуют непосредственно из выражений для булевых функций, реализуемых схемой.

Задача синтеза заключается в построении из заданного набора логических элементов комбинационной схемы, реализующей заданную систему булевых функций.

Решение задачи синтеза не является однозначным, можно предложить различные варианты комбинационных схем, реализующих одну и ту же систему булевых функций, но отличающихся теми или иными параметрами. Разработчик комбинационных схем из этого множества вариантов выбирает один, исходя из дополнительных критериев: минимального количества логических элементов, необходимых для реализации схемы, максимального быстродействия и т.д. Существуют различные методы синтеза комбинационных схем, среди которых наиболее разработан канонический метод.