Лок вычисления производной Derivative

рактическая работа №3

Библиотека блоков Simulink: Continuous – аналоговые блоки

Цель работы:изучить библиотеку блоков Continuous. Понять принцип действия блоков, изучить их параметры.

Назначение блоков библиотеки: реализуют непрерывные функции.

лок вычисления производной Derivative

Назначение:

Выполняет численное дифференцирование входного сигнала.

Параметры:

Нет.

Для вычисления производной используется приближенная формула Эйлера:

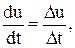
где Du – величина изменения входного сигнала за время Dt; Dt – текущее значение шага модельного времени.

Значение входного сигнала блока до начала расчета считается равным нулю. Начальное значение выходного сигнала также полагается равным нулю.

Точность вычисления производной существенно зависит от величины установленного шага расчета. Выбор меньшего шага расчета улучшает точность вычисления производной.

На рисунке 1 показан пример использования дифференцирующего блока для вычисления производной прямоугольного сигнала. В рассматриваемом примере, для повышения наглядности, шаг расчета выбран достаточно большим.

Данный блок используется для дифференцирования аналоговых сигналов. При дифференцировании дискретного сигнала с помощью блока Derivative его выходной сигнал будет представлять собой последовательность импульсов соответствующих моментам времени скачкообразного изменения дискретного сигнала.

2. Интегрирующий блок lntegrator

Назначение:

Выполняет интегрирование входного сигнала.

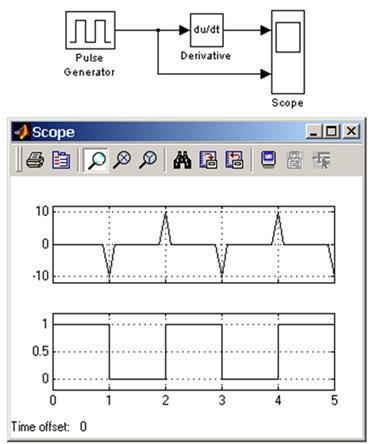
Рисунок 1 – Использование блока Derivative для дифференцирования сигнала

EX_derivative_1.zip

Параметры:

1) External reset – Внешний сброс. Тип внешнего управляющего сигнала, обеспечивающего сброс интегратора к начальному состоянию. Выбирается из списка:

- none – нет (сброс не выполняется),

- rising – нарастающий сигнал (передний фронт сигнала),

- falling – спадающий сигнал (задний фронт сигнала),

- either – нарастающий либо спадающий сигнал,

- level – не нулевой сигнал (сброс выполняется если сигнал на управляющем входе становится не равным нулю);

В том случае, если выбран какой-либо (но не none), тип управляющего сигнала, то на изображении блока появляется дополнительный управляющий вход. Рядом с дополнительным входом будет показано условное обозначение управляющего сигнала.

2) Initial condition source – Источник начального значения выходного сигнала. Выбирается из списка:

- internal – внутренний;

- external – внешний.

В этом случае на изображении блока появляется дополнительный вход, обозначенный x0, на который необходимо подать сигнал задающий начальное значение выходного сигнала интегратора;

3) Initial condition – Начальное условие. Установка начального значения выходного сигнала интегратора. Параметр доступен, если выбран внутренний источник начального значения выходного сигнала;

4) Limit output (флажок) – Использование ограничения выходного сигнала;

- Upper saturation limit – Верхний уровень ограничения выходного сигнала. Может быть задан как числом, так и символьной последовательностью inf, то есть + ¥;

- Lower saturation limit – Нижний уровень ограничения выходного сигнала. Может быть задан как числом, так и символьной последовательностью inf, то есть - ¥;

5) Show saturation port – управляет отображением порта, выводящего сигнал, свидетельствующий о выходе интегратора на ограничение. Выходной сигнал данного порта может принимать следующие значения:

1. Ноль, если интегратор не находится на ограничении;

2. +1, если выходной сигнал интегратора достиг верхнего ограничивающего предела;

3. -1, если выходной сигнал интегратора достиг нижнего ограничивающего предела.

6) Show state port (флажок) – Отобразить/скрыть порт состояния блока. Данный порт используется в том случае, если выходной сигнал интегратора требуется подать в качестве сигнала обратной связи этого же интегратора. На пример, при установке начальных условий через внешний порт или при сбросе интегратора через порт сброса. Выходной сигнал с этого порта может использоваться также для организации взаимодействия с управляемой подсистемой.

7) Absolute tolerance – Абсолютная погрешность.

На рисунке 2 показан пример работы интегратора при подаче на его вход ступенчатого сигнала. Начальное условие принято равным нулю.

Пример на рисунке 3 отличается от предыдущего подачей начального значения через внешний порт. Начальное значение выходного сигнала в данном примере задано равным –10.

Пример на рисунке 4 демонстрирует использование входного порта для сброса выходного сигнала и порта состояния интегратора с целью организации обратной связи.

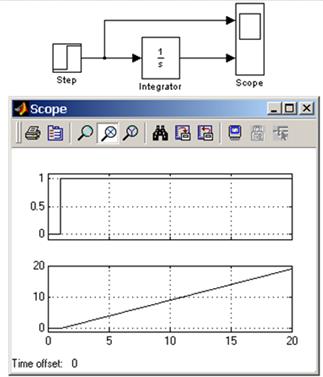
Рисунок 2 – Интегрирование ступенчатого сигнала

EX_integrator_1.zip

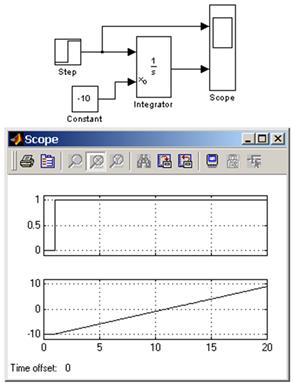
Рисунок 3 – Интегрирование ступенчатого сигнала с установкой начального значения выходного сигнала

EX_integrator_2.zip

Схема работает следующим образом: входной постоянный сигнал преобразуется интегратором в линейно-изменяющийся, по достижении выходным сигналом значения равного 1 блок Relational Operator вырабатывает логический сигнал, по переднему фронту которого происходит сброс выходного сигнала интегратора до начального значения равного нулю. В результате на выходе интегратора формируется пилообразный сигнал, изменяющийся от 0 до +1.

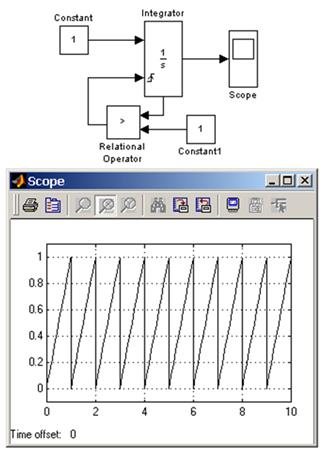
Рисунок 4 – Генератор пилообразного сигнала на основе интегратора

EX_integrator_3.zip

Следующая схема (рис.5) использует установку начального значения интегратора с помощью его выходного сигнала. В первый момент времени начальное значение выходного сигнала интегратора с помощью блока IC (Initial Condition) устанавливается равным нулю. По достижении выходным сигналом значения равного 1 блок Relational Operator подает сигнал сброса выходного сигнала интегратора на начальный уровень, при этом сигналом, задающим начальный уровень, оказывается инвертированный выходной сигнал интегратора (т.е. -1). Далее цикл работы схемы повторяется. В отличие от предыдущей схемы выходным сигналом генератора является двуполярный сигнал.

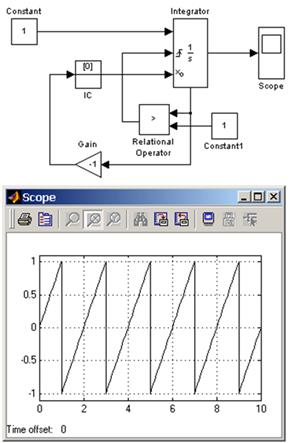
Рисунок 5 - Генератор двуполярного пилообразного сигнала на основе интегратора

EX_integrator_4.zip

3. Блок Memory

Назначение:

Выполняет задержку входного сигнала на один временной такт.

Параметры:

- Initial condition – начальное значение выходного сигнала.

- Inherit sample time (флажок) – наследовать шаг модельного времени. Если этот флажок установлен, то блок Memory использует шаг модельного времени (Sample time) такой же, как и в предшествующем блоке.

На рисунке 6 показан пример использования блока Memory для задержки дискретного сигнала на один временной такт.

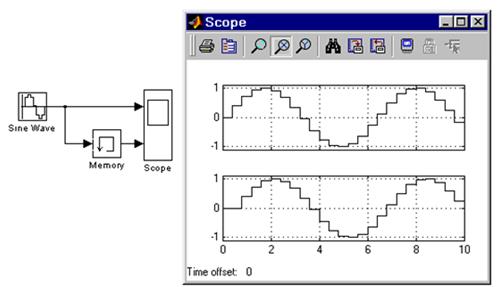
Рисунок 6 – Применение блока для задержки сигнала на один временной такт

EX_memory_1.zip

4. Блок фиксированной задержки сигнала Transport Delay

Назначение:

Обеспечивает задержку входного сигнала на заданное время.

Параметры:

1) Time Delay – Время задержки сигнала (не отрицательное значение);

2) Initial input – Начальное значение выходного сигнала;

3) Buffer size – Размер памяти, выделяемой для хранения задержанного сигнала. Задается в байтах числом, кратным 8 (по умолчанию 1024);

4) Pade order (for linearization) – Порядок ряда Паде, используемого при аппроксимации выходного сигнала. Задается целым положительным числом.

При выполнении моделирования значение сигнала и соответствующее ему модельное время сохраняются во внутреннем буфере блока Transport Delay. По истечении времени задержки значение сигнала, извлекается из буфера и передается на выход блока. В том случае, если шаги модельного времени не совпадают со значениями моментов времени для записанного в буфер сигнала, блок Transport Delay выполняет аппроксимацию выходного сигнала.

В том случае, если начального значения объема памяти буфера не хватит для хранения задержанного сигнала, Simulink автоматически выделит дополнительную память. После завершения моделирования в командном окне MATLAB появится сообщение с указанием нужного размера буфера.

На рисунке 7 показан пример использования блока Transport Delay для задержки прямоугольного сигнала на 0.5 с.

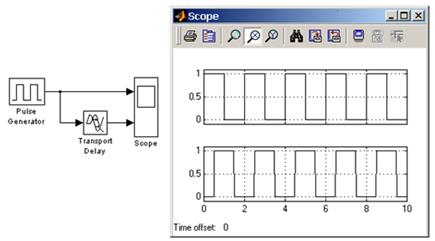
Рисунок 7 - Пример использования блока Transport Delay для задержки сигнала

EX_Trans_delay_1.zip

5. Блок управляемой задержки сигнала Variable Transport Delay

Назначение:

Выполняет задержку входного сигнала, заданную величиной сигнала управления.

Параметры:

1) Maximum delay – Максимальное значение времени задержки сигнала (не отрицательное значение);

2) Initial input – Начальное значение выходного сигнала;

3) Buffer size – Размер памяти, выделяемой для хранения задержанного сигнала. Задается в байтах числом, кратным 8 (по умолчанию 1024);

4) Pade order (for linearization) – Порядок ряда Паде, используемого при аппроксимации выходного сигнала. Задается целым положительным числом.

Блок управляемой задержки Variable Transport Delay работает аналогично блоку постоянной задержки сигнала Transport Delay.

В том случае, если значение управляющего сигнала задающего величину задержки превышает значение, заданное параметром Maximum delay, то задержка выполняется на величину Maximum delay.

На рисунке 8 показан пример использования блока Variable Transport Delay. Величина времени задержки сигнала изменяется от 0.5 c до 1 с в момент времени равный 5 с.

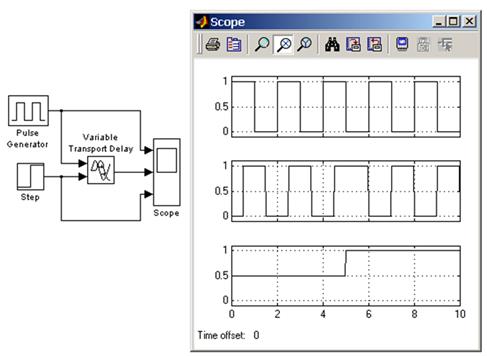
Рисунок 8 – Пример использования блока Variable Transport Delay

EX_Var_Trans_delay_1.zip

6. Блок передаточной функции Transfer Fcn

Назначение:

Блок передаточной характеристики Transfer Fcn задает передаточную функцию в виде отношения полиномов:

,

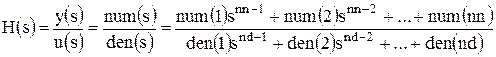где nn и nd – порядок числителя и знаменателя передаточной функции; num – вектор или матрица коэффициентов числителя; den – вектор коэффициентов знаменателя.

Параметры:

1) Numerator – вектор или матрица коэффициентов полинома числителя;

2) Denominator – вектор коэффициентов полинома знаменателя;

3) Absolute tolerance – Абсолютная погрешность.

Порядок числителя не должен превышать порядок знаменателя.

Входной сигнал блока должен быть скалярным. В том случае, если коэффициенты числителя заданы вектором, то выходной сигнал блока будет также скалярным (как и входной сигнал). На рисунке 9 показан пример моделирования колебательного звена с помощью блока
Transfer Fcn.

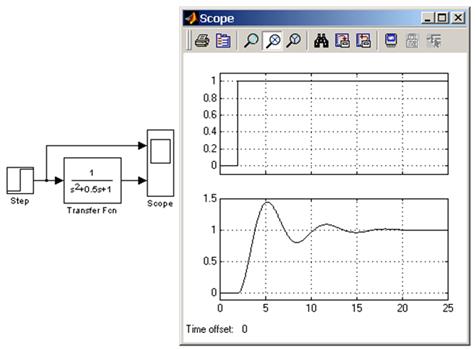
Рисунок 9 – Пример моделирования колебательного звена

EX_Trancfer_Fcn_1.zip

Если коэффициенты числителя заданы матрицей, то блок Transfer Fcn моделирует векторную передаточную функцию, которую можно интерпретировать как несколько передаточных функций имеющих одинаковые полиномы знаменателя, но разные полиномы числителя. При этом выходной сигнал блока является векторным и количество строк матрицы числителя задает размерность выходного сигнала.

На рисунке 10 показан пример блока Transfer Fcn задающий векторную передаточную функцию. Там же показана модель полностью аналогичная рассматриваемой по своим свойствам, но состоящая из отдельных блоков Transfer Fcn.

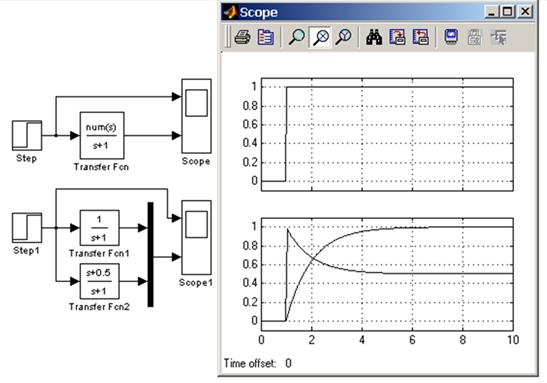
Рисунок 10 – Пример моделирования векторной передаточной функции и ее аналог

EX_Trancfer_Fcn_2.zip

Начальные условия при использовании блока Transfer Fcn полагаются нулевыми. Если же требуется, чтобы начальные условия не были нулевыми, то необходимо с помощью функции tf2ss (инструмент Control System Toolbox) перейти от передаточной функции к модели в пространстве состояний и моделировать динамический объект с помощью блока State-Space.

7. Блок передаточной функции Zero-Pole

Назначение:

Блок Zero-Pole определяет передаточную функцию с заданными полюсами и нулями:

,

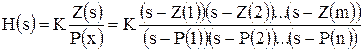где Z – вектор или матрица нулей передаточной функции (корней полинома числителя); P – вектор полюсов передаточной функции (корней полинома знаменателя); K – коэффициент передаточной функции, или вектор коэффициентов, если нули передаточной функции заданы матрицей. При этом размерность вектора K определяется числом строк матрицы нулей.

Параметры:

1) Zeros – Вектор или матрица нулей;

2) Poles – Вектор полюсов;

3) Gain – Скалярный или векторный коэффициент передаточной функции;

4) Absolute tolerance – Абсолютная погрешность.

Количество нулей не должно превышать число полюсов передаточной функции.

В том случае, если нули передаточной функции заданы матрицей, то блок Zero-Pole моделирует векторную передаточную функцию.

Нули или полюса могут быть заданы комплексными числами. В этом случае нули или полюса должны быть заданы комплексно-сопряженными парами полюсов или нулей, соответственно.

Начальные условия при использовании блока Zero-Pole полагаются нулевыми.

На рисунке 11 показан пример использования блока Zero-Pole. В примере передаточная функция имеет один действительный нуль и два комплексно-сопряженных полюса.

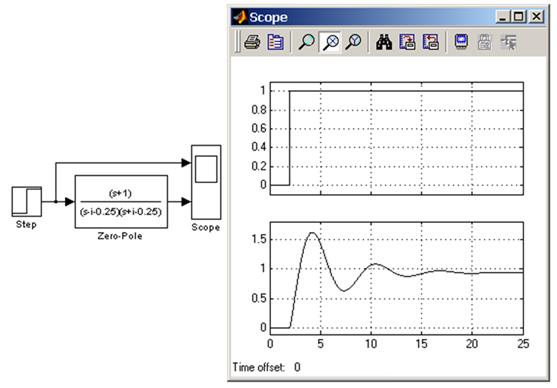
Рисунок 11 – Пример использования блока Zero-Pole

8. Блок модели динамического объекта State-Space

Назначение:

Блок создает динамический объект, описываемый уравнениями в пространстве состояний:

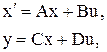
где x – вектор состояния; u – вектор входных воздействий; y – вектор выходных сигналов; A, B, C, D – матрицы: системы, входа, выхода и обхода, соответственно.

Размерность матриц показана на рисунке 12 (n – количество переменных состояния, m – число входных сигналов, r – число выходных сигналов).

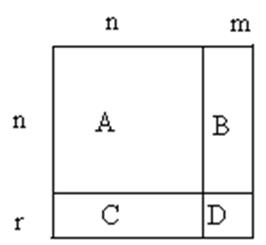
Рисунок 12 – Размерность матриц блока State-Space

Параметры:

1) A –Матрица системы;

2) B – Матрица входа;

3) C – Матрица выхода;

4) D – Матрица обхода;

5) Initial condition – Вектор начальных условий;

6) Absolute tolerance – Абсолютная погрешность;

На рисунке 13 показан пример моделирования динамического объекта с помощью блока State-Space. Матрицы блока имеют следующие значения:

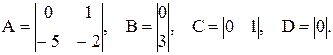
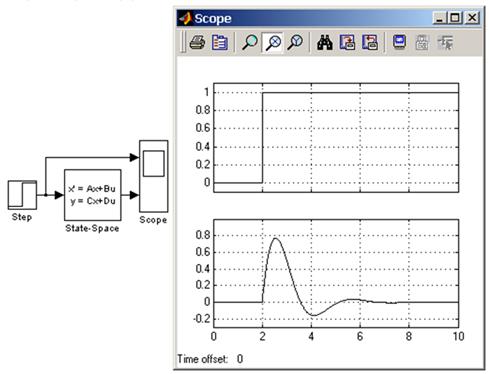
Рисунок 13 – Пример использования блока State-Space

EX_State_Space_1.zip

Контрольные вопросы.

1. В чем состоит назначение блоков библиотеки Continuous?

2. Назовите назначение блока Integrator?

3. Что такое настройка Limit output блока Integrator?

4. Назовите назначение блока Memory?

5. Назовите назначение блока Transport Delay?

6. Назовите назначение блока Variable Transport Delay?

7. Назовите назначение блока Transfer Fcn?

8. Назовите назначение блока Zero-Pole?

9. Назовите назначение блока State-Space?