Представление чисел в памяти

Числа, записанные в двоичной системе счисления, могут быть представлены в ЦВМ в формах с фиксированной и с плавающей запятой.

Разрядная сетка (т.е. схематическое представление ячейки памяти) для формы с фиксированной запятой состоит из знакового и цифровых разрядов, представляющих совокупность целой части числа и, отделенной от нее запятой, дробной части. Место запятой фиксировано, поэтому для целой и дробной частей числа выделяется конкретное количество разрядов отведенного поля памяти. У положительных чисел в знаковом разряде стоит "0", у отрицательных - "1".

При выполнении арифметических операций могут получаться результаты, целая часть которых содержит больше цифр, чем число разрядов, отведенных для хранения целой части числа. В этом случае происходит ситуация ²переполнение разрядной сетки². Для уменьшения вероятности переполнения разрядной сетки запятая обычно фиксируется перед старшим цифровым разрядом, т.е. допускается работа только с правильными дробями. Эта форма используется только в специальных случаях.

Пример

Ниже приведено представление правильной десятичной дроби 0,256 в форме с фиксированной запятой

+	256 . . . 0

Другим способом представления чисел в ЦВМ является запись в форме с плавающей запятой, в которой для изображения чисел используется форма

N = m ´ p^q ,

где m - мантисса (цифровая часть числа);

p - основание системы счисления;

q - порядок числа.

При этом для мантиссы m должно выполняться условие ½m½<1. Если мантисса числа, представленного в форме с плавающей запятой, удовлетворяет условию 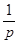£ m < 1, то число называют нормализованным. Нормализация числа осуществляется сдвигом числа влево и соответствующим уменьшением его порядка.

Пример

Представить число с плавающей точкой

- 0,1010010100 @ 10¹¹ , где 10 означает 2₁₀ .

В память машины это число будет записано в следующем виде:

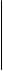
1 1010010100 0 00011

знак

числа порядок

знак порядка

мантисса

Кодирование чисел для выполнения

Арифметических операций

Представление чисел в ПЭВМ зависит от способа их кодирования. Используют 3 способа кодирования числовой информации:

- прямой код;

- дополнительный код;

- обратный код.

Положительные числа при любом способе кодирования изображаются одинаково, т.е. так, как они записаны. Знак числа изображается дополнительным разрядом, который записывается перед старшим разрядом числа. Прямой код может использоваться для выполнения операций сложения положительных чисел и умножения чисел с произвольными знаками на основании правил двоичного сложения и умножения (см. выше). Для реализации операции сложения чисел, имеющих разные знаки, разработаны специальные коды: дополнительный и обратный.

Положительные числа в дополнительном коде изображаются без изменений, также как в прямом. Для получения дополнительного кода отрицательного числа выполняются следующие операции:

- в знаковом разряде числа записывается 1;

- во всех числовых разрядах числа нули заменяются на единицы и единицы на нули;

- к младшему разряду прибавляется единица.

Если число положительное, то обратный код совпадает с прямым. Для получения отрицательного числа в обратном коде выполняется следующая последовательность действий:

- запись в знаковом разряде 1;

- замена в цифровых разрядах числа нулей на единицы и единиц на нули.