Примеры бинарных отношений. 1 страница

КОНСПЕКТ ЛЕКЦИЙ

По дисциплине

«ДИСКРЕТНАЯ МАТЕМАТИКА»

для студентов всех форм обучения

направления 6.050101 – «Компьютерные науки»

Электронное издание

УтвержДено

кафедрой «ИУС»

Протокол № 1 от 29.08.2013 г.

кафедрой «ИИ»

Протокол № 1 от 31.08.2013 г.

ХАРЬКОВ 2013

Конспект лекций по дисциплине «Дискретная математика» для студентов всех форм обучения направления 6.050101 – «Компьютерные науки» [Электронное издание] / Состав. Н.В. Васильцова, Л.Э. Чалая. – Харьков: ХНУРЭ, 2013. – 293 с.

Составители Н.В. Васильцова

Л.Э. Чалая

СОДЕРЖАНИЕ

Лекция 1. Основы теории множеств. Основные понятия и обозначения теории множеств.. 10

1.1 Интуитивное понятие множества. 10

1.2 Элементы множества. 10

1.3 Конечные, бесконечные, счетные множества. 12

1.4 Пустое и универсальное множества. 13

1.5 Мощность множества. 14

1.6 Способы задания множеств. 15

1.7 Множество и подмножество. 18

1.8. Контрольные вопросы и задания. 20

Лекция 2 Алгебра множеств.. 20

2.1 Геометрическая интерпретация множеств. Круги Эйлера и диаграммы Венна 20

2.2 Операции на множествах. 22

2.3 Общее определение алгебры.. 25

2.4 Понятие алгебры множеств. Аксиомы алгебры множеств. 27

2.5 Принцип двойственности. 28

2.6 Тождественные преобразования формул алгебры множеств. 29

2.7 Контрольные вопросы и задания. 29

Лекция 3 Отношения и их свойства. Отношения и операции над ними. 30

3.1 Декартово произведение множеств. 30

3.2 Понятие отношений. Бинарные и n-арные отношения. 32

3.3 Область определения и область значений отношений. 33

3.4 Способы задания отношений. 34

3.5 Операции над отношениями. 38

3.6 Контрольные вопросы и задания. 40

Лекция 4 Свойства бинарных отношений.. 41

4.1 Основные свойства бинарных отношений. 41

4.2 Классы бинарных отношений. 43

4.3 Контрольные вопросы и задания. 50

Лекция 5 Функциональные отношения. Элементы реляционной алгебры.. 50

5.1 Функциональные отношения. 50

5.2 Элементы реляционной алгебры.. 54

5.3 Контрольные вопросы и задания. 61

Лекция 6. Двузначная логика. Булевы функции. Основные понятия 62

6.1 Двузначная логика. 62

6.2 Булевы переменные и функции. 62

6.3 Область определения и область значений булевой функции. 64

6.4 Способы задания булевых функций. 66

6.5 Реализация булевых функций формулами. 70

6.6 Принцип двойственности. 72

6.7 Булевы алгебры. Законы и тождества булевой алгебры.. 74

6.8 Контрольные вопросы и задания. 78

Лекция 7. Нормальные формы булевых функций.. 79

7.1 Нормальные формы булевых функций, основные понятия. 79

7.3 Теоремы о разложениях булевой функции по переменным. 83

7.4 Переход от табличного представления функции к алгебраическому представлению функции. 85

7.5 Правила преобразования произвольной формулы алгебры логики в нормальную форму с использованием законов булевой алгебры.. 87

Лекция 8. Минимизация булевых функций.. 88

8.1 Основные понятия минимизации булевых функций. Критерии минимизации. 88

8.3 Основные методы минимизации булевых функций. Метод минимизирующих карт (диаграммы Карно-Вейча) 92

8.4 Контрольные вопросы и задания. 98

Лекция 9. Алгебра Жегалкина и линейные функции. Функциональная полнота наборов булевых функций.. 98

9.1 Алгебра Жегалкина и линейные функции. 98

9.2 Функциональная полнота булевых функций. 102

9.3 Контрольные вопросы и задания. 109

Лекция 10. Логика высказываний. Алгебра высказываний. 109

10.1 Высказывания (основные понятия) 109

10.3 Алгебра логики и логика высказываний. 114

10.4 Интерпретация формул логики высказываний. Правильные рассуждения 115

10.5 Логическая эквивалентность и логическое следствие. 117

10.6 Контрольные вопросы и задания. 118

Лекция 11. Исчисление высказываний.. 119

11.1 Основные понятия исчисления высказываний. 119

11.2 Аксиомы и полнота исчисления логики высказываний. 119

11.3 Выводимость в исчислении высказываний. 120

11.4 Непротиворечивость, независимость. 122

11.5 Различные аксиоматизации исчисления высказываний. 123

11.6 Некоторые приемы доказательств в исчислении высказываний. 124

11.7 Контрольные вопросы и задания. 125

Лекция 12. Логика предикатов (логика первого порядка). Предикаты. Алгебра предикатов.. 125

12.1 Основные понятия логики предикатов. 125

12.2 Операции логики предикатов. Кванторные операции. 128

12.3 Формулы и их интерпретация в логике предикатов. 129

12.4 Законы и тождества логики предикатов. 132

12.5 Предваренные нормальные формы.. 133

12.6 Выводимость в логике предикатов. 134

12.7 Контрольные вопросы и задания. 135

Лекция 13. Исчисление предикатов.. 135

13.1 Основные понятия исчисления предикатов. 135

13.2 Аксиомы исчисления предикатов. 136

13.3 Правила вывода в исчислении предикатов. 136

13.4 Контрольные вопросы и задания. 137

Лекция 14. Общие определения комбинаторики. Основные правила комбинаторики. Модели типовых комбинаторных конфигураций. 137

14.1 Общие определения комбинаторики. Понятие 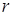-выборки. Общие задачи комбинаторики. 137

14.2 Основные правила комбинаторики. 139

14.3 Модели комбинаторных конфигураций. 140

14.4 Контрольные вопросы и задания. 145

Лекция 15. Принцип включения и исключения.. 146

15.1 Теорема и формула включений и исключений. 146

15.2 Решето Эратосфена. 147

15.3 Частный случай теоремы о включениях и исключениях. 147

15.3 Контрольные вопросы и задания. 148

Лекция 16. Задачи о распределении предметов по урнам (урновые схемы решения комбинаторных задач) 148

16.1 Задачи о размещении предметов. 148

16.3 Распределение n одинаковых предметов по k урнам. 149

16.4 Распределение разных предметов без учета порядка предметов по урнам 149

16.5 Распределение разных предметов с учетом их порядка в урнах. 149

16.6 Распределение разных предметов между одинаковыми урнами при условии, что урны не пусты.. 150

16.7 Композиции. 156

16.8 Комбинаторика разбиений. 156

16.9 Контрольные вопросы и задания. 157

Лекция 17. Подходы к изучению комбинаторных объектов и чисел 157

17.1 Понятие продуктивной функции. 157

17.2 Рекуррентные соотношения в комбинаторике. 159

17.3 Контрольные вопросы и задания. 161

Лекция 18. Происхождение графов. Определение графов.. 161

18.1 Разновидности графов. Неориентированный граф. Определения. 161

18.2 Ориентированный граф. Определения. 163

18.3 Основные термины для ориентированных и неориентированных графов 163

18.4 Способы задания графов. 169

18.5 Контрольные вопросы и задания. 175

Лекция 19. Операции над графами. Изоморфизм графов. Плоские и планарные графы.. 176

19.1 Операции над графами. 176

19.2 Гомеоморфные графы.. 182

19.3 Плоские и планарные графы.. 182

9.4 Контрольные вопросы и задания. 189

Лекция 20. Связность графов. Эйлеровы и гамильтоновы графы 189

20.1 Связность графов, компонента связности. n-связный граф. 189

20.2 Свойства связных графов. 191

20.3 Компоненты сильной связности ориентированного графа. 191

20.4 Алгоритм выделения компонент сильной связности. 192

20.5 Метрические характеристики связных графов. 194

20.6 Эйлеровы графы.. 198

20.7 Алгоритм нахождения эйлерова цикла (алгоритм Флери) 200

20.8 Гамильтоновы графы.. 200

20.9 Алгоритм Робертса-Флореса (метод перебора Робертса-Флореса) нахождения гамильтоновых циклов в графе. 201

20.10 Признаки существования гамильтоновых циклов, путей и контуров. 204

20. 11 Контрольные вопросы и задания. 205

Лекция 21 Деревья.. 205

21.1 Определение и свойства деревьев. 205

21.2 Свойства деревьев. 206

21.3 Перечисление графов. 206

21.4 Перечисление деревьев. 208

21.5 Остовы графа. 209

21.6 Алгоритмы построения остовов графа. 210

21.7 Ориентированные и бинарные деревья. Определения. 213

21.8 Правила прохождения бинарных деревьев. 215

21.9 Эквивалентные бинарные деревья. 216

21.10 Контрольные вопросы и задания. 217

Лекция 22. Цикломатика графов. Раскраска графов.. 217

22.1 Цикломатика графов. 217

22.2 Раскраска графов. 223

22.3 Контрольные вопросы и задания. 230

Лекция 23. Транспортные сети и потоки. Их свойства.. 230

23.1 Кратчайшие расстояния и пути в графах. 230

23.2 Алгоритм Дейкстры поиска кратчайших путей. 231

23.3 Алгоритмы поиска кратчайших путей между всеми парами вершин графа 236

23.4 Транспортные сети и потоки. 238

УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО ДИСЦИПЛИНЕ. 249

Основная литература. 249

Дополнительная литература. 250

Глоссарий терминов дисциплины.. 251

Лекция 1. Основы теории множеств. Основные понятия и обозначения теории множеств

1.1 Интуитивное понятие множества

Понятие множества является одним из наиболее общих математических понятий и как любое другое исходное понятие математической теории оно не определяется точно. Поэтому вместо строгого определения понятия «множество» обычно принимается некоторое основное положение о множестве и его элементах, дается описательное определение, содержание и смысл которого раскрываются при изучении теории множеств. Рассматривая основное положение о множестве и его элементах, чаще всего пользуются определением, предложенным основателем теории множеств немецким математиком Георгом Кантором, который определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией и мыслью».

Математическое понятие «множество» связано с абстракцией. Сущность этой абстракции множества заключается в том, что действительно существующие связи объединяемых объектов между собой и с другими объектами игнорируются, а вместо них объединяемым объектам приписываются новые связи друг с другом, выражающие их принадлежность множеству. При этом считается, что два объекта, ничем не отличающиеся друг от друга, являются одним и тем же объектом.

1.2 Элементы множества

Определение. Рассмотрим множество как совокупность объектов произвольной природы, которые удовлетворяют двум свойствам:

- все объекты этой совокупности попарно различимы;

- существует некий признак принадлежности объекта этой совокупности.

Определение. Объекты, которые образуют множество, называются элементами (членами) этого множества.

Пример.

– множество натуральных чисел с нулем;

– множество натуральных чисел;

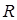– множество всех действительных чисел;

– множество всех решений уравнения , то есть ;

A  множество прямых, проходящих через заданную точку.

Пример. В качестве признака принадлежности объекта некоторой совокупности (множеству) могут быть следующие свойства (признаки): «быть цифрой», «быть буквой», «быть числом», «быть словом», «быть служебным символом», «быть идентификатором данного», «быть кодом операции» и т.п.

Для обозначения конкретных множеств в общем виде используются различные заглавные буквы или заглавные буквы с индексами, например, . Для обозначения элементов множеств в общем виде используются различные строчные буквы или строчные буквы с индексами .

Утверждение, что множество состоит из различных элементов (и только из этих элементов), условно записывается , т.е. множество обозначается скобками {…}, внутри которых либо просто перечисляются элементы, либо описываются их свойства.

Пример. ; .

Элементами множеств могут быть другие множества, тогда эти элементы обозначаются заглавными буквами.

Пример. , где , , .

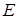. Множество состоит из трех элементов: .

Определение.Множество, элементами которого являются множества, обычно называются классом или семейством.

Семейства множеств обычно обозначают прописными «рукописными» буквами латинского алфавита, чтобы отличить их от множеств, не содержащих множеств в качестве элементов.

Если есть один из объектов множества , то говорим, что есть элемент , или принадлежит . Принадлежность элемента множеству записывается как . Если не является элементом , это записывается как . Символ 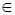называется символом принадлежности.

Пример. , но .

Поскольку множество однозначно определяется только элементами, которые оно содержит, порядок перечисления элементов между фигурными скобками произвольный, т.е. , но многократная запись одного и того же элемента – не желательна, т. е. .

Определение. При многократной записи одного и того же элемента множество называют мультимножествоми применяют особые методы анализа.

С точки зрения теории множеств, множество и его мультимножество – это один и тот же объект, и они могут между собой не различаться. Однако часто, особенно когда речь идет о представлении множества в памяти вычислительной машины, возникает потребность отличать мультимножество от множества.

Определение. Множество, в котором важны не только его элементы, но и порядок их следования во множестве, называется упорядоченным.

Определение. Конечное множество называется упорядоченным, если его элементы пронумерованы.

Упорядоченное множество обозначают, как правило, либо круглыми, либо треугольными скобками.

Определение. Кортеж(вектор) - это упорядоченный набор элементов . Элементы, образующие кортеж, называются координатами или компонентами. Координаты нумеруются слева направо.

Определение. Число координат кортежа (вектора) называется длиной или размерностью кортежа (вектора).

Пример.

- упорядоченное множество, состоящее из 4-х элементов (кортеж длины 4);

, где

Пример.Пусть - множество географических координат долготы и широты . Если поменять местами долготу и широту, то в результате можно попасть в другую точку света.

1.3 Конечные, бесконечные, счетные множества

Множество может содержать любое число элементов – конечное или бесконечное.

Определение.Если множество содержит конечное число элементов, его называют конечным, в противном случае множество называется бесконечным.

Пример. Множество действительных решений квадратичного неравенства конечно, если , и бесконечно, если .

Примеры конечных множеств:

- множество цифр ;

- множество страниц в книге.

Примеры бесконечных множеств:

- множество натуральных чисел;

- множество окружностей на плоскости.

Определение. Множество называется счетным, если его объекты можно пересчитывать (каждому объекту множества присвоить натуральное число, которое было бы номером лишь одного элемента множества).

Пример. Множество цифр счетно и конечно, а множество целых чисел – счетно, но не конечно.

1.4 Пустое и универсальное множества

В теории множеств используются понятия «пустого множества» и «универсального множества».

Определение. Множество, не содержащее ни одного элемента, называется пустым и обозначается специальным символом .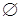

Пример. Пусть – множество действительных решений квадратного уравнения . Множество конечно, Если дискриминант отрицателен, множество пусто.

Пример. Множество выигрышей в следующем тираже спортлото на купленные билеты может оказаться пустым.

Пример. Неизвестно, является ли пустым или нет множество всех решений в целых числах уравнения .

Пустое множество введено в математике для удобства и единообразия языка. Роль пустого множества 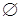аналогична роли числа нуль. Если исследуется множество объектов, обладающих каким-либо свойством, и впоследствии выясняется, что таких объектов не существует, то гораздо удобнее сказать, что исследуемое множество пусто, чем объявлять его несуществующим. Понятие пустого множества может быть использовано для определения заведомо несуществующей совокупности элементов. Пустое множество будем условно относить к конечным счетным множествам.

Пример. Множество действительных корней уравнения является пустым множеством.

Введем понятие универсального множества.

Определение. Универсальное множество (или универсум), которое обозначают символом 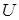, есть множество, содержащее все элементы, принимающие участие в решении определенного класса задач.

Обычно уже в самом определении конкретного множества явно или неявно ограничивается совокупность допустимых объектов, однако данную совокупность удобнее зафиксировать явным образом, определив её в качестве универсума в рамках решаемой задачи.

Примеры. Так, множество слонов следует искать среди млекопитающихся, а не среди рыб.

Если речь идет о множестве чисел, делящихся на 3, то ясно, что оно является множеством целых чисел.

В теории чисел универсум обычно совпадает с множеством всех целых или натуральных чисел.

В математическом анализе универсум может быть множеством всех действительных чисел или множеством всех точек -мерного пространства.

Универсумом зоологии является мир животных; универсумом лингвистики – слова и т.д.

1.5 Мощность множества

При сравнении множеств по числу содержащихся в них элементов возникает понятие мощности множества.

Определение. Мощностьконечного счётного множества есть число его элементов , которое обозначают как .

Пример. Мощность множества цифр десятичной системы счисления равна 10.

Мощность множества строчных букв латинского алфавита – 26.

Мощность пустого множества равна нулю ( ), а мощность множества равна 1, т.е. .

Определение.Если , то множества и называются равномощными.

1.6 Способы задания множеств

Чтобы задать множество, нужно указать, какие элементы ему принадлежат.

Существует несколько основных способов задания (описания) множеств:

- словесное (вербальное) описание элементов множеств и их основных характеристик;

- простое перечисление элементов множества;

- описание множества с использованием схемы свертывания (указанием характерных свойств элементов множества или характеристической функции множества, заданием порождающей процедуры).

Рассмотрим каждый из перечисленных способов.

Словесное (вербальное) описание элементов множеств и их характеристик используется чаще всего для пояснения и осуществления доказательств основных положений данной теории при решении конкретных задач (применяется в разговорной речи, оформлении различного рода научной и технической документации и т.п.).

Пример.Спецификация задает множество деталей изделия.

Каталог – множество книг в библиотеке.

Простое перечисление элементов множества (неупорядоченного) между фигурными скобками используется, в основном, для описания конечных множеств.

Пример.

есть множество, содержащее натуральные числа 1, 2, 3 и 4.

есть множество продуктов питания.

Множество гласных букв можно представить как .

– множество решений уравнения .

– множество остатков при делении целых чисел на 7.

Иногда перечислением элементов задают и бесконечное множество. Это делают в тех случаях, когда ясен алгоритм последовательного порождения элементов.

Пример. Множество положительных целых чисел можно обозначить как .

Множество первых n положительных целых чисел обозначается , где точками показано продолжение перечисления элементов.

описывает множество квадратов всех положительных чисел, которые меньше или равны .

описывает множество кубов всех положительных чисел.

Очевидно, что перечисление элементов удобно (целесообразно) только в том случае, когда множество элементов имеет их ограниченное количество или произвольный элемент характеризуется свойством, которое легко описать.

Если же множество имеет, хотя и конечное, однако, большое количество элементов, такое задание множества достаточно громоздко, а в случае бесконечного множества его применение вообще невозможно.

Пример. Используя способы перечисления не так легко описать, например, множество граждан Украины и совершенно немыслимо описать множество действительных чисел.

В общем случае множества можно задавать (описывать) по так называемой схеме свертывания. Схема свертывания может быть реализована при помощи: