Обработка и представление результатов измерений

8.1. Обработке результатов измерений предшествует этап их анализа.

8.1.1. Если при анализе процесса измерений удалось установить источник появления промахов (неверное действие оператора, падение напряжения в электрической сети, магнитные бури и др. причины), то их исключают перед обработкой результатов измерений.

8.1.2. Если причины появления промахов неизвестны, для решения вопроса возможности их исключения используют статистические критерии (см. пп. 3.2.2, 3.2.3).

8.1.3. Обнаруженные систематические погрешности измерения (систематические погрешности средств измерений, метода, оператора, из-за воздействия влияющих факторов) вносят в результаты измерений в виде поправок, а неисключенные систематические и случайные погрешности составляют погрешность результата измерений.

8.2. Обработка прямых однократных измерений проводится в соответствии с МИ 1552–86 «ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений». Обработка прямых многократных измерений – в соответствии с ГОСТ 8.207–76. Обработка косвенных измерений – в соответствии с МИ 2083–90 «Измерения косвенные. Определение результатов измерений и оценивание их погрешностей». Обработка результатов сличений при совокупных измерениях изложена в МИ 1832–88 «ГСИ. Сличения групп средств поверки одинакового уровня точности. Основные правила».

8.3. Результаты измерений в зависимости от цели измерительной задачи могут быть представлены числом, в виде таблицы, графика и другом виде.

Формы представления результатов измерений и их погрешностей должны соответствовать МИ 1317–86 «ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроля их параметров».

8.4. Погрешность результата измерений выражают, как правило, одной значащей цифрой. Две значащие цифры в погрешности результата измерения сохраняют: при точных измерениях; если первая значащая цифра не более трех; если предел допускаемой погрешности задан двумя значащими цифрами.

ПРИЛОЖЕНИЕ 1

Справочное

Квантили распределения Т (q, n)

n	q
0,01	0,02	0,05	0,10
	1,73	1,72	1,71	1,69
	1,97	1,96	1,92	1,87
	2,16	2,13	2,07	2,00
	2,31	2,26	2,18	2,09
	2,43	2,37	2,27	2,17
	2,53	2,46	2,35	2,24
	2,62	2,54	2,41	2,29
	2,75	2,66	2,52	2,39
	2,86	2,76	2,60	2,46
	2,95	2,84	2,67	2,52
	3,02	2,90	2,73	2,58
	3,08	2,96	2,78	2,62
	3,13	3,01	2,82	2,66
	3,18	3,05	2,86	2,70
	3,22	3,09	2,90	2,73
	3,26	3,12	2,93	2,76
	3,29	3,16	2,96	2,79
	3,42	3,28	3,08	2,90
	3,52	3,37	3,16	2,99

ПРИЛОЖЕНИЕ 2

Справочное

КРИТЕРИЙ АББЕ

Группа результатов измерений содержит постоянно возрастающую или постоянно убывающую систематическую погрешность, если выполняется неравенство

,

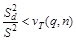где S_d – среднее квадратическое отклонение группы результатов измерений, вычисленное по формуле

,

S – среднее квадратическое отклонение группы результатов измерений, вычисленное по формуле

;

n	– число измерений в группе;
Xi	– i-й результат измерений группы;
vT(q, n)	– квантиль распределения, соответствующий уровню значимости q и числу измерений n в группе.

Значения v_T(q, n) в зависимости от уровня значимости q и числа измерений n представлены в таблице.

Квантили распределения v_T (q, n)

Число измерений, n
Уровень значимости, q	0,01	0,31	0,28	0,33	0,37	0,41	0,45	0,47	0,50
0,05	0,39	0,44	0,49	0,53	0,56	0,59	0,61	0,63

Число измерений, n
Уровень значимости, q	0,01	0,52	0,54	0,56	0,60	0,62	0,65	0,68	0,71
0,05	0,65	0,66	0,68	0,71	0,73	0,75	0,77	0,79

ПРИЛОЖЕНИЕ 3

Справочное

Квантили распределения Стьюдента t(q, f)

Число степеней свободы, f
Уровень значимости, q	0,050	2,4	2,1	2,0	1,9	1,9	1,9	1,8	1,8	1,8	1,8	1,7
0,025	3,2	2,8	2,6	2,4	2,4	2,3	2,3	2,2	2,2	2,1	2,1
0,005	5,8	4,6	4,0	3,7	3,5	3,4	3,2	3,2	3,1	3,0	2,9

Число степеней свободы, f
Уровень значимости, q	0,050	1,7	1,7	1,7	1,7	1,7	1,7	1,7	1,7	1,7
0,025	2,1	2,1	2,1	2,1	2,1	2,0	2,0	2,0	2,0
0,005	2,9	2,8	2,8	2,8	2,8	2,8	2,8	2,7	2,7

ПРИЛОЖЕНИЕ 4

Справочное

Таблица 1

Квантили распределения F_0,05

Число степеней свободы, f2	Число степеней свободы, f1
									¥
	19,0	19,2	19,2	19,3	19,3	19,4	19,4	19,4	19,5	19,5
	9,55	9,28	9,12	9,01	8,94	8,85	8,74	8,69	8,58	8,53
	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,84	5,70	5,63
	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,60	4,44	4,37
	5,14	4,76	4,53	4,39	4,28	4,15	4,00	3,92	3,75	3,67
	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,49	3,32	3,23
	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,20	3,02	2,93
	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,99	2,80	2,71
	4,10	3,71	3,48	3,33	3,22	3,07	2,91	2,83	2,64	2,54
	3,68	3,29	3,06	2,90	2,79	2,64	2,48	2,38	2,18	2,07
	3,49	3,10	2,87	2,71	2,60	2,45	2,28	2,18	1,97	1,84
	3,39	2,99	2,76	2,60	2,49	2,34	2,16	2,07	1,84	1,71
	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,99	1,76	1,62
	3,26	2,87	2,64	2,48	2,37	2,22	2,04	1,94	1,70	1,57
	3,23	2,84	2,61	2,45	2,34	2,18	2,00	1,90	1,66	1,51
	3,21	2,81	2,58	2,42	2,31	2,15	1,97	1,87	1,63	1,48
	3,18	2,79	2,56	2,40	2,29	2,13	1,95	1,85	1,60	1,44
¥	3,00	2,60	2,37	2,21	2,10	1,94	1,75	1,64	1,35	1,00

Таблица 2

Квантили распределения F_0,01

Число степеней свободы, f2	Число степеней свободы, f1
										¥
	99,0	99,2	99,2	99,3	99,3	99,4	99,4	99,4	99,5	99,5	99,5
	30,8	29,4	28,7	28,2	27,9	27,5	27,1	26,8	26,6	26,4	26,1
	18,0	16,7	16,0	15,5	15,2	14,8	14,4	14,2	13,9	13,7	13,5
	13,3	12,1	11,4	11,0	10,7	10,3	9,89	9,68	9,47	9,24	9,02
	10,9	9,78	9,15	8,75	8,47	8,10	7,72	7,52	7,31	7,09	6,88
	9,55	8,45	7,85	7,46	7,19	6,84	6,47	6,28	6,07	5,86	5,65
	8,65	7,59	7,01	6,63	6,37	6,03	5,67	5,48	5,28	5,07	4,86
	8,02	6,99	6,42	6,06	5,80	5,47	5,11	4,92	4,73	4,52	4,31
	7,56	6,55	5,99	5,64	5,39	5,06	4,71	4,52	4,33	4,12	3,91
	6,36	5,42	4,89	4,56	4,32	4,00	3,67	3,49	3,29	3,08	2,87
	5,85	4,94	4,43	4,10	3,87	3,56	3,23	3,05	2,86	2,64	2,42
	5,57	4,68	4,18	3,85	3,63	3,32	2,99	2,81	2,62	2,40	2,17
	5,39	4,51	4,02	3,70	3,47	3,17	2,84	2,66	2,47	2,25	2,01
	5,27	4,40	3,91	3,59	3,37	3,07	2,74	2,56	2,37	2,13	1,90
	5,18	4,31	3,83	3,51	3,29	2,99	2,66	2,48	2,29	2,06	1,80
	5,11	4,25	3,77	3,45	3,23	2,94	2,61	2,43	2,23	1,99	1,75
	5,06	4,20	3,72	3,41	3,19	2,89	2,56	2,38	2,18	1,95	1,68
¥	4,61	3,78	3,32	3,02	2,80	2,51	2,18	2,00	1,79	1,52	1,00

ПРИЛОЖЕНИЕ 5

Справочное

КРИТЕРИЙ ВИЛКОКСОНА

Из двух групп результатов измерений: х₁,…, x_n; y₁,…, y_m, n ³ m ³ 5 составляют вариационный ряд, в котором все n + m значений х₁,…, x_n; y₁,…, y_m располагают в порядке их возрастания и приписывают им ранги – порядковые номера членов вариационного ряда. Различие средних допустимо, если выполняется неравенство

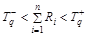
где Ri	– ранг xi, равный его номеру в вариационном ряду;
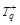,	– нижнее и верхнее критические значения для выбранного уровня q.

При m £ 15 критические значения , 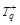определяют по таблице. При m > 15 критические значения , 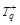вычисляют но формулам:

;

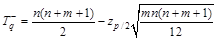где z_p/2 – квантиль нормированной функции Лапласа.

КРИТЕРИЙ СИДЖЕЛА-ТЬЮКИ

Рассеивание средних квадратических отклонений групп допустимо, если выполняется неравенство

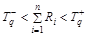
где R_i – ранг x_i, определяемый следующим образом. В вариационном ряду из (n + m) значений x и y (n ³ m ³ 5) приписывают ранг 1 наименьшему значению, ранг 2 – наибольшему, ранг 3 – предыдущему наибольшему значению, ранг 4 – второму после наименьшего значению, ранг 5 – третьему после наименьшего значению, ранг 6 –третьему перед наибольшим значению и т.д. Критические значения , 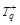определяют по таблице.

Критические значения , и ,

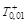
n

m

ПРИЛОЖЕНИЕ 6

Справочное

Квантили распределения X² (q, f)

Число степеней свободы, f = L – 1
Уровень значимости, q	0,01	11,3	13,3	16,8	20,1	23,2	26,2	29,1	32,0	34,8
0,05	7,8	9,5	12,6	15,5	18,3	21,0	23,7	26,3	28,9
0,10	6,2	7,8	10,6	13,4	16,0	18,5	21,1	23,5	26,0

Число степеней свободы, f = L – 1
Уровень значимости, q	0,01	37,6	40,3	43,0	45,6	50,9	57,3	63,7	70,0	76,1
0,05	31,4	33,9	36,4	38,9	43,8	49,8	55,8	61,7	67,5
0,10	28,4	30,8	33,2	35,6	40,3	46,1	51,8	57,5	63,2

ЛИТЕРАТУРА

1. Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. – М.: Финансы и статистика, 1982.

2. НТМ СЭВ 1–84. Методы обработки результатов прямых измерений с многократными наблюдениями.

3. Линник Ю.В. Способ наименьших квадратов и основы теории обработки наблюдений. – М.: Физматгиз, 1958.

4. Welch В.L. The generalization of Student's problem when several different population variances are involved. Biometrika, 34, 1947, 28–35.

5. Хальд А. Математическая статистика с техническими приложениями. – M. 1956.

6. Кудряшова Ж.Ф. Выявление условий проведения однократных измерений на основе анализа их погрешностей. Сборник научн. трудов, – Л.: Энергоатомиздат, 1986.

7. Труды метрологических институтов СССР. Выпуск 134 (194). – М.: Изд-во стандартов, 1972.