Оценка случайных погрешностей
Адекватным математическим аппаратом описания случайных погрешностей является теория вероятностей. Согласно последней случайная величина наиболее полно характеризуется законом распределения (или плотностью распределения) вероятностей. Измерителям чаще всего приходится принимать нормальную и равномерную плотности распределения. Возможны и другие законы распределения, которые обычно аппроксимируются стандартными функциями. Если выполняются предположения о том, что погрешности измерений могут принимать непрерывный ряд значений и при большом числе измерений частота появления погрешностей, равных по абсолютной величине, но имеющих различный знак, одинакова и малые погрешности встречаются чаще, чем большие, то для описания случайных погрешностей следует применять нормальный закон распределения вероятностей, для которого
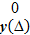 =
= 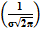 exp
exp 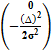 , (2.2)
, (2.2)
где 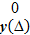 — плотность вероятностей случайной погрешности
— плотность вероятностей случайной погрешности 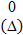 ; σ — среднее квадратичное значение случайной погрешности.
; σ — среднее квадратичное значение случайной погрешности.
Кривые, соответствующие выражению (2.2) для разных значений σ, приведены на (рис. 2.1), из которого видно, что при малых значениях σ вероятней получить малую погрешность измерений, нежели при больших значениях σ.
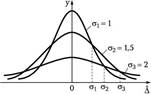
Рис. 2.1. Нормальный закон распределения случайных погрешностей
Вероятность того, что погрешность результата измерений находится между заданными предельными значениями 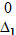 и
и 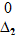 , вычисляется по формуле
, вычисляется по формуле
P( 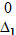 ≤
≤ 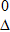 ≤
≤ 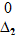 ) =
) = 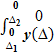 d
d 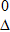 =
= 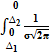 ехр
ехр 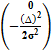 d
d 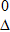 . (2.3)
. (2.3)
Интеграл в формуле (2.3) можно вычислить, используя таблицы функции Лапласа
Ф(z) = 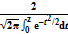 ,
,
приводимые в книгах по теории вероятностей и статической обработке экспериментальных результатов.
Нетрудно заметить, что вероятность
P( 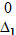 ≤
≤ 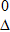 ≤
≤ 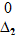 ) =
) =  [Ф(
[Ф( 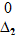 /σ) ‒ Ф(
/σ) ‒ Ф( 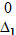 /σ)].
/σ)].
В табл. 2.1 приведены значения вероятностей для некоторых интервалов [ 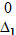 ,
, 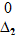 ], заданных в единицах σ. В первой графе табл. 2.1 указываются интервалы, которые характеризуются нижними и верхними границами
], заданных в единицах σ. В первой графе табл. 2.1 указываются интервалы, которые характеризуются нижними и верхними границами 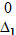 и
и 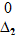 соответственно. Во второй графе показаны вероятности P того, что случайная погрешность результата измерений не выходит за границы соответствующих интервалов. В третьей графе представлены вероятности выхода случайной погрешности за пределы интервалов.
соответственно. Во второй графе показаны вероятности P того, что случайная погрешность результата измерений не выходит за границы соответствующих интервалов. В третьей графе представлены вероятности выхода случайной погрешности за пределы интервалов.
Таблица 2.1. Значения вероятностей P для некоторых интервалов, заданных в единицах σ
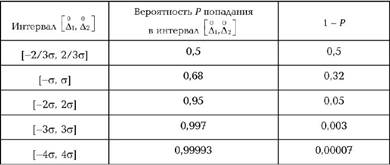
Согласно табл. 2.1 вероятности получения значения случайных погрешностей в интервале [‒2/3σ, +2/3σ] и за его пределами одинаковы, в то время как в среднем только 0,3% измерений имеют погрешности, абсолютное значение которых превышает 3σ. Значение погрешности 2/3σ называется вероятной погрешностью, а значение 3σ часто считают наибольшей возможной погрешностью. Однако при числе измерений 20-30 (n > 1) максимальная погрешность нередко может превышать 3σ.
Суммирование погрешностей. При измерениях может быть несколько источников как систематических, так и случайных погрешностей. Поэтому практически важным является вопрос о правилах нахождения суммарной погрешности измерений по известным значениям погрешностей составляющих ее частей. При суммировании составляющих неисключенной систематической погрешности их конкретные реализации можно рассматривать как реализации случайной величины. Если известны границы составляющих неисключенной систематической погрешности — Θi, а распределение этих составляющих в пределах границ равномерно, то граница неисключенной систематической погрешности результата измерения Θ вычисляется по формуле
Θ = k 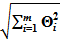 ,
,
где k — коэффициент, определяемый принятой доверительной вероятностью; при доверительной вероятности 0,95 он принимается равным 1,1; m — число неисключенных систематических погрешностей.
При суммировании случайных погрешностей необходимо учитывать их корреляционные связи. Суммарная средняя квадратичная погрешность — σ∑ при двух составляющих может быть вычислена по формуле
σ∑ = 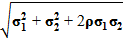 , (2.4)
, (2.4)
где σ1 и σ2 — средние квадратичные погрешности отдельных составляющих; ρ — коэффициент корреляции.
Поскольку на практике трудно получить удовлетворительную оценку коэффициента корреляции ρ, приходится ограничиваться крайними случаями, т.е. считать, что либо ρ = 0, либо ρ = ±1. Тогда формула (2.4) примет следующий вид:
σ∑ = 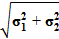 , если ρ = 0,
, если ρ = 0,
или
σ∑ = |σ1 ± σ2|, если ρ = ±1.
Таким образом, при отсутствии корреляционной связи средние квадратичные погрешности складываются геометрически, а в случае жесткой корреляционной зависимости — алгебраически. Этот вывод справедлив и для случая нескольких источников погрешностей.
Исключение грубых погрешностей. Выделение грубых погрешностей (промахов) — непростая задача, она требует глубокого понимания особенностей поведения измеряемой величины. Наиболее часто для обнаружения промаха используют так называемый критерии Райта. Согласно этому критерию, если случайное отклонение какого-либо измерения от среднего арифметического значения превышает 3σ, то считают, что данное измерение содержитпромах. Критерий Райта в таком виде целесообразно применять при не очень большом числе измерений (5 < n < 20). Если же число измерений 20 < n < 100, то рекомендуется вместо значения 3σ использовать значение 4σ.
Необходимое число измерений. Вопрос о необходимом числе измерений весьма важен, так как от его решения зависит весь последующий ход эксперимента. С увеличением числа измерений можно уменьшить только случайную составляющую погрешности, т.е. средние квадратичные погрешности σ и σср, которые зависят от числа измерений n. В то же время систематическая погрешность не снижается при увеличенииn. Поэтому если остаточная систематическая погрешность является преобладающей, то увеличение числа измерений практически не дает уменьшения погрешности. В этом случае чаще всего ограничиваются одним измерением. При более точных измерениях основными могут являться случайные погрешности. Тогда проведение многократных измерений будет оправданным. Число измерений нужно выбирать таким образом, чтобы средняя квадратичная случайная погрешность σср не превышала максимального допустимого значения σср.доп. Однако уменьшения σср за счет многократных измерений следует добиваться только до тех пор, пока вклад случайных погрешностей в общую погрешность измерения не будет сравним с вкладом остаточных систематических погрешностей.
