Краткий теоретический материал

Задание № 1.

Даны множества и . Найти:

а) , б) , в) , г) , д) .

, .

Решение.

Найдем все элементы множеств и .

Решим уравнение

.

Положим

.

Тогда

.

В новой переменной уравнение записывается в виде

,

;

1) ,

2 ) ,

.

Следовательно,

.

Решим неравенство

в множестве натуральных чисел:

.

Решим второе из неравенств:

,

.

Из найденных значений выберем такие, которые удовлетворяют неравенству :

(удовлетворяет),

(удовлетворяет),

(не удовлетворяет),

(не удовлетворяет),

(удовлетворяет),

(удовлетворяет).

Следовательно,

.

Выполним теперь требуемые действия над множествами и , которые являются ответом для данного задания:

а) ;

б) ;

в) ;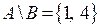

г) ;

д) .

Задание № 2.

Доказать равенство множеств.

.

Решение.

Доказательство равенства двух множеств состоит из доказательства двух включений: а) и б) .

а) Доказательство включения :

.

б) Доказательство включения :

.

Задание № 3.

Дано бинарное отношение на множестве . Найти:

а) ;

б) ;

г) ;

д) ;

е) ;

ж) .

и делит , .

Решение.

Найдем все элементы бинарного отношения :

.

Из этого представления видно, что среди первых элементов пар, составляющих множество , участвуют все элементы множества . Поэтому область определения бинарного отношения совпадает со всем множеством: .

Среди вторых элементов пар, составляющих множество , участвуют все элементы множества . Поэтому область значений бинарного отношения совпадает со всем множеством: .

Поменяв местами, первый элемент со вторым во всех парах, получим обратное отношение :

.

Так как:

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то .

Суперпозиция состоит из тех же элементов, что и множество , Поэтому .

Так как

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то .

Следовательно, имеем

.

Заметим, что в суперпозицию не входят следующие пары: .

Так как

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то ;

и , то .

Следовательно, суперпозиция совпадает с множеством :

.

Задание № 4. С помощью равносильных формул (элементарных тавтологий) доказать тождественно истинность данной формулы (При решении ссылаться на номер формулы из перечня равносильных формул).

Решение.

Запишем данную формулу:

;

применим формулу 10:

;

последовательно применим формулу 22:

;

;

;

применим формулы 15 и 21:

;

;

;

применим формулу 6:

;

применим формулу 17:

;

применим формулу 12:

;

и, наконец, применяя формулу 17 окончательно, получим:

,

что и требовалось доказать.

Задание № 5. Используя основные тавтологии, построить равносильные данной формуле ДНФ и КНФ. (При решении ссылаться на номер формулы из перечня равносильных формул).

Решение.

Запишем данную формулу:

;

дважды применим формулу 22:

;

применим формулу 24:

;

дважды применим формулу 22:

;

дважды применим формулу 15:

;

дважды применим формулу 21:

;

дважды применим формулу 5:

;

дважды применим формулы 1 и 7:

;

дважды применим формулу 10:

.

Получена КНФ, равносильная данной формуле. Продолжим процесс для получения равносильной КНФ.

Последовательно применим формулы 18 и 13:

;

;

последовательно применим формулы 1 и 2:

;

;

применим формулу 26:

.

Получена ДНФ, равносильная данной формуле.

Ответ: – ДНФ;

– КНФ.

Задание № 6. Построив таблицу истинности данной формулы, построить равносильные ей СДНФ и СКНФ.

Решение.

Построим таблицу истинности данной формулы:

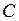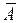							Итог

Для построения СДНФ обратимся к значениям «1» в столбце «Итог». Каждому значению «1» сопоставим одну ПЭК по следующему правилу: переменная ( или 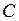) в ПЭК входит сама, если значение этой переменной в этой строке «1» и её отрицание, если значение этой переменной в этой строке «0». Имеем:

;

;

;

;

;

.

Следовательно,

.

– СДНФ – равносильная данной формуле.

Для построения СКДНФ обратимся к значениям «0» в столбце «Итог». Каждому значению «0» сопоставим одну ПЭД по следующему правилу: переменная ( или 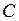) в ПЭК входит сама, если значение этой переменной в этой строке «0» и её отрицание, если значение этой переменной в этой строке «1». Имеем:

;

;

Следовательно,

– СКНФ – равносильная данной формуле.

Ответ:

– СДНФ;

– СКНФ.

Задание № 7. Для данной формулы алгебры высказываний построить многочлен Жегалкина.

.

Решение.

Каждой формуле алгебры высказываний соответствует один многочлен Жегалкина. Равносильным формулам соответствует один и тот же многочлен Жегалкина. Обратно, каждому многочлену Жегалкина соответствует формула алгебры высказываний. Однако обратное соответствие не является однозначным. Одному многочлену Жегалкина может соответствовать несколько равносильных формул.

Упростим данную формулу (естественно, если упрощение возвожно). Запишем данную формулу:

;

дважды применим формулу 15 (первый закон де Моргана):

;

дважды применим формулу 21 (закон снятия двойного отрицания):

;

применим формулу 21 (расставим двойное отрицание):

;

последовательно избавимся от операции отрицания; к верхнему отрицанию применим формулу :

;

применим формулу 15:

;

дважды применим формулу :

;

дважды применим формулу :

;

дважды применим формулу :

.

перемножим скобки, применяя формулу :

.

упростим сумму, применяя формулы , и :

.

Ответ: – многочлен Жегалкина.

Задание № 8. Упростить данную релейно-контактную схему.

Решение.

Составим функцию проводимости данной релейно-контакт-ной схемы. Для этого рассмотрим две простейшие релейно-кон-тактные схемы:

где и – отдельные участки релейно-контактной схемы.

Участки и примем за формулу, а замкнутость участка – за истинность формулы, разомкнутость – за ложность. Тогда данным схемам соответствуют функции проводимости:

а) ;

б) .

Если верхний участок схемы обозначим , а нижний , то данной в условии задачи схеме соответствует функция проводимости пункта а) . Теперь применяя это правило для отдельных схем и , получим:

,

.

Упростим эти формулы. Используем формулу 6 (закон дистрибутивности конъюнкции относительно дизъюнкции):

;

;

используем формулу 2:

;

;

используем формулы 8 и 18:

;

;

используем формулы 14 и 13:

;

;

формула – упрощена; используем формулы 12 и 6:

;

используем формулы 11 и 12:

;

формула – упрощена.

Таким образом, функцией проводимости данной релейно-контакт-ной схемы, является

.

По полученной формуле составим упрощенную релейно-контактную схему, которая является ответом для данной задачи:

Краткий теоретический материал

Основные понятия теории множеств

Понятие множества относится к числу фундаментальных неопределяемых понятий математики. Под понятием множества будем понимать любую определенную совокупность объектов. Объекты, из которых состоит множество, называются элементами множества. Множества обозначаются заглавными латинскими буквами, а их элементы – прописными. Если объект является элементом множества , то используется обозначение: , если же объект не является элементом множества , то используется обозначение: .

Множество, не содержащее элементов, называется пустым и обозначается .

Если множество состоит из элементов , то используется обозначение . В этом случае будем говорить, что множество задано перечислением его элементов.

Обозначения для некоторых, часто используемых, множеств:

– множество натуральных чисел;

– множество целых чисел;

– множество вещественных чисел.

Множество можно задавать и с помощью характеристического предиката. Например, множество рациональных чисел можно записать следующим образом:

.

Два множества и называются равными, если они состоят из одних и тех же элементов и обозначается .

Если каждый элемент множества является также элементом множества , то множество называется подмножеством множества и обозначается :

.

Приведем ещё одно определение равенства двух множеств и . Два множества и называются равными, если каждое из них являются подмножеством другого:

.

Операции над множествами

Объединением двух множеств и называется множество, если оно содержит только все элементы множества и все элементы множества . Объединение множеств и обозначается :

.

Пересечениемдвух множеств и называется множество, если оно содержит только все элементы, принадлежащие множествам и одновременно. Пересечение множеств и обозначается :

.

Разностью двух множеств и называется множество, если оно содержит только все элементы множества (первого множества), не принадлежащие множеству (второму множеству):

.

Бинарное отношение

Прямым произведением двух множеств и называется множество всех пар элементов, первый из которых принадлежит множеству (первому множеству), а второе –множеству (второму множеству):

:

Бинарным отношением между элементами двух множеств и называется любое подмножество множества : .

Пусть является бинарным отношением между элементами двух множеств и . Областью определениябинарного отношения называется множество

.

Областью значенийбинарного отношения называется множество

.

Обратным отношениемдля бинарного отношения называется множество

.

Пусть является бинарным отношением между элементами множеств и , а является бинарным отношением между элементами множеств и 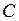. Суперпозициейбинарных отношений и называется бинарное отношение

.