Формулы исчисления предикатов

1.Какое из выражений не будет формулой и почему ? Исправьте ошибки и определите, какими – свободными или связанными – будут все вхождения переменных в полученных формулах. Установите области действия всех кванторов.

а) ((a) Ú ($ x P(x));б) (a Ú ($ x P(x));г) ((" x P(x, y)) Ú Q(x));д) (P(x) Ù 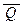(y));

д) (P(x) Ú Q(y, z)); е) ($ t Q(x) ® (" z P(z, t))); ж)(($ x P(x, y)) « (" y P(x, y)));

з) (" x 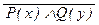); и) (a ® ($ y R(x))); к) 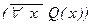; л) .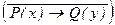

2.Определите, какими – свободными или связанными – будут все вхождения переменных в формулах, установите области действия всех кванторов:

а) ((a Ú b) ® ($ x P(x, y))); б) ( 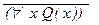® (" x P(x, y))); в) P(x) Ú ($ x P(x));

в) (((" P(x, y)) Ú P(x, x)) ® ($ y (P(x, y) Ù Q(x, y))))); г) ($ x (P(x) Ú (a ®b)) Ù P(x));

д) (" x ($ y (P(z, y) Ù (" z Q(z, x)))) ® R(x, z)); е) ( Ú (" z P(x, z))).

3.Формулы какого вида записываются одним символом алфавита ИП ? Какое наименьшее количество символов алфавита ИП потребуется, чтобы записать следующую по сложности формулу ИП ? Формулы какого вида остаются формулами, если дописать некоторый один символ алфавита ИП ? Есть ли формулы ИП, записываемые четырьмя, символами алфавита ИП ? А пятью ?

4.В следующих выражениях всеми способами так расставьте скобки, чтобы получились формулы:

а) $ y P x, y Ú S x ; б) a Ú b ® c; в) a Ù " y P x;г) a Ù " y R y ® Q x, y ;

д) 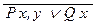® a ® $ x P x, y ® Q x ;е) R x « " z R z Ú P x, x .

5.Задайте предикаты и запишите в виде формул ИП следующие утверждения:

а) найдётся целое число x, для которого при любом действительном y существует такое целое число z, что y ³ z;

б) если x > y, то для любого z верно z×x > z×y;

в) если целое число x , а y – действительное, и x ³ y, то найдётся целое число z и действительное t со свойством z t;

г) если 5 < 2, то найдётся такое целое число, которое больше своего квадрата при условии, что его квадрат меньше нуля;

д) любое целое число из отрезка [0; 1] меньше всякого нецелого числа, большего 10;

е) в том случае, когда число больше своего квадратного корня, можно утверждать, что это число неотрицательное;

е) для того, чтобы произвольное целое число было положительным необходимо и достаточно, чтобы это число совпадало со своим модулем;

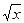ж) 0 < или же найдётся ³ 0;

з) если квадрат целого числа положителен, то из того, что это число больше двух следует, что корень из него неположителен при условии, что любое неотрицательное число неположительно;

6.Задайте предикаты и запишите в виде формул ИП следующие утверждения:

а) нулеван положе корефана или же найдётся корефан помарчее нулевана;

б) любая понтажная чечка вихлястей непонтажной штуковинки;

в) найдётся ксёлик, для которого при любом игулике существует ксёлик полаханней игулика;

г) в том случае, когда мозлик болдажнее своего тюлика, этот мозлик болдажнее и кувальчика;

д) для того, чтобы дрючка была понтажной необходимо и достаточно, чтобы эта дрючка была незавязной;

е) если вырик и мамлютка зашканные, то найдётся вырик и мамлютка незамастые.

Интерпретации формул

1.Найдите ошибки в следующих интерпретациях формул:

а) ($ x P(x, y)), J = (M = N, a = 1, P(x, y) = (x > y));

б) (a ® ((" x P(x)) ® P(y))), J = (M = {0}, a = 5, P(x , y) = (x £ y));

в) ($ x P(x, y)), J = (M = N, P(x) = (x > 1));

г) (a ® ((" x P(x)) ® P(y))), J = (M = {0}, a = 1, P(x) = (x > 0));

д) (($ x P(x, y)) ® (" y (P(x, y) Ú Q(y)))), J = (M = {1}, P(x, y)=(x | y), Q(y)=(y = 1));

е) ($ x P(x, y)), J = (M = R, P(x, y) = ( 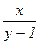> 2));

ж) (P(x) ® Q(x, y)), J = (M = R, x = 1, y = 1+i, P(x) = (x > 2), Q(x, y)=(y = 1));

з) (P(x, y) ® P(y, x)), J = (M = R, x = 1, y = 1, P(x, y) = (x > y), P(y, x)=(y = 1));

и) (" x (P(x, y) ® ($ y (P(y, y) Ú P(y, x))))), J = (M = R, x = 1, y = 0, P(x, y) = (x | y)).

2.Вычислите значения формул при интерпретациях:

а) (" x Q(x, y)), J = (M = N, y = 1, Q(x, y) = (x ³ y));

б) (" x Q(x, y)), J = (M = {0, 1}, y = 0, Q(x, y) = (x > y));

в) (" x (Q(x, y) ® P(x)), J = (M = N, y = 2, Q(x, y) = (x = y), P(x) = (x ¹ 1));

г) (" x (Q(x, y) ® P(x)), J = (M = N, y = 2, Q(x, y) = (x = y), P(x) = (x ³ 1));

д) (b ® (($ x R(x)) ® R(y))), J = (M = {0, 1}, b = 0, y = 1, R(x) = (x ¹ 0));

е) (b ® (($ x R(x)) ® R(y))), J = (M = {0, 1}, b = 1, y = 1, R(x) = (x > 1));

ж) (($ x R(x, y)) ® R(y, x))), J = (M = {0, 1}, y = 1, ,x = 1, R(x, y) = (x > y));

з) (($ x R(x, y)) ® R(y, x)), J = (M = {0, 1}, y = 0, x = 1, R(x, y) = (x > y));

и) (P(x) ® ($ y P(y))), J = (M = R, x = 0, P(x) = (x > 0));

к) (P(x) ® ($ y P(y))), J = (M = R, x = 1, P(x) = (x > 0)).

3.Классифицируйте формулы: а) (P(x) Ú Q(x)); б) (Q(x) ® Q(y)); в) (a Ù ($ x R(x, y)));

г) (a « ($ x P(x, y))); д) (($ x Q(x)) Ù (" y (Q(y) Ú Q(x)))); е) ((" y R(y)) ® R(x));

ж) ($ x (" y (P(x, y) ® Q(x)))); з) ((" x (" y S(x, y))) ® S(z, z)); и) (P(x) ® );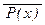

к) 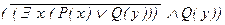; л) ((" x R(x)) ® R(y));м) (P(x) ® (a ® P(x))).

4.Являются ли следующие формулы тождественно истинными ?

а) (P(x) ® P(y));б) (($ x R(x)) Ú 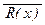);в) ((" x S(x)) ® ($ y S(y))); г) (a Ú P(x));

д) (a Ú (P(x) Ú 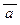));е) ((" x (" y Q(x, y))) ® (" x Q(x, x)));ж) (R(x) ® (" x R(x)));

з) (" x ((P(x) ® 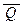(x)) ® )); и) ( Ù A(x));

к) ® 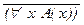; л) (($ x (P(x) ® Q(x))) « ((" x P(x)) ® ($ x Q(x))).

5.Являются ли следующие формулы выполнимыми ?

а) (P(x) Ù Q(x)); б) (Q(x) « Q(y)); в) (" x (R(x) Ú S(x))); г) ($ x (P(x, y) Ú R(x))); д) (" x (($ y P(x, y)) Ú R(z))); е) 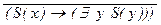; ж) ® ($ x P(x));

з) ((" x (P(x) ® a)) Ú ($ x (P(x) ® 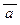)));и) ((" z T(z)) Ú (a Ù ).

6.Расставьте скобки так, чтобы полученные формулы не были выполнимыми:

а) $ x P(x) Ú 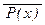;б) R(x) ® " y P(y) ® R(x);в) " x S(x) ® S(y);е) a Ú P(x); д) " x S(x) ® 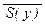;е) $ y Q(y, x) ® Q(x, y) Ú " x Q(x, x) Ù .

7.Приведите примеры выполнимых формул ИП, но тождественно ложных при любой интерпретации на а)одноэлементном множестве; б)двухэлементном множестве.

8.Существует ли формула ИП, истинная при интерпретации на любом двухэлементном множестве, но ложная при интерпретации на любом трёхэлементном множестве ?