Понятие двоичной функции и способа ее задания.

МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ

для студентов факультета повышения квалификации

Москва 2016

План УМД 2015/2016 уч. г.

Методические указания

и контрольные задания

по курсу

МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ

Составители: В.О. Мелихов, доцент

А.Н Кироев, аспирант.

В данной методической разработке приведены бюджет времени студента, рабочая программа, содержание лекций и упражнений, методические указания по разделам курса, задания на контрольные работы.

Издание утверждено на заседании кафедры.

Отв.редактор В.Н.Шакин, доцент

Рецензент д.т.н. И.П Кузнецов.

Содержание

Введение.................................................................................................................................... 4

1. Математическая логика....................................................................................................... 6

1.1. Понятие двоичной функции и способа ее задания.................................................... 6

1.2. Одноместные и двухместные двоичные функции..................................................... 7

1.3. Алгебра двоичных функций......................................................................................... 9

1.4. Совершенная дизъюнктивная нормальная форма.................................................... 11

1.5. Совершенная конъюнктивная нормальная форма.................................................... 12

1.6. Базисы функций алгебры логики............................................................................... 12

1.7. Полином Жегалкина.................................................................................................... 13

1.8. Существенные и несущественные переменные....................................................... 14

1.9. Минимизация функций алгебры логики................................................................... 15

1.9.1. Структурный метод карт Карно........................................................................... 15

1.9.2. Метод Блейка......................................................................................................... 18

2. Основы теории алгоритмов.............................................................................................. 22

2.1. Понятие алгоритма и связанных с ним категорий................................................... 22

2.2. Машина Тьюринга....................................................................................................... 22

2.3. Тезис Тьюринга............................................................................................................ 25

2.3.1. Композиция МТ..................................................................................................... 25

2.3.2. Разветвление МТ.................................................................................................... 25

2.4. Вычислительная сложность алгоритмических проблем.......................................... 26

Список рекомендуемой литературы.................................................................................... 28

Правило выбора варианта Контрольных работ и пример выполнения........................... 29

Контрольная работа................................................................................................................ 31

Введение

Целью данного курса является освоение теоретических основ таких разделов дискретной математики как Математическая логика и Теория алгоритмов. Курс "Математическая логика и Теория алгоритмов" посвящен изуче­нию элементов математического аппарата, предназначенного для описания дискретно изменяющихся величин, объектов, систем и процессов таких, например, как вычислительные системы и процессы. Изучение курса включает освоение фундаментальных понятий алгебры логики, теории формальных алгоритмов и вычислительной сложности.

В соответствии с содержанием курса данный сборник включает две части, посвященные соответственно изучению функций алгебры логики и теоретических основ формальных алгоритмов. Организация учебного материала, представленного в сборнике, полностью соответствует стандарту изложения математических дисциплин для инженерно-технических и вычислительных спе­циальностей и направлений подготовки. Объем учебных задач и требования к их выполнению позволяют получить необходимые практические навыки в работе с функциями алгебры логики, а также изучить свойства формальных алгоритмов.

Постановке контрольных заданий предшествует краткое изложение теоретического материала. По каждому из разделов приводятся ссылки на рекомендуемые для изучения литературные источники.

Изучение Математической логики в рамках дисциплины включает определение функций алгебры логики (ФАЛ) и способов их задания. Устанавливается связь ФАЛ с импульсными схемами. Учащиеся осваивают алгоритмы построения ФАЛ в виде совершенных формы и полинома Жегалкина. Определяется понятие базисного набора ФАЛ, доказывается эквивалентность базисов. Исследуется существенность двоичных переменных. Подробно рассматриваются вопросы структурной и аналитической минимизации ФАЛ.

На основе полученных представлений фундаментальное понятие алгоритма характеризуется с позиций теории формальных алгоритмических моделей и вычислительной сложности.

В рамках дисциплины студенты знакомятся с возможностями описания алгоритмов по Тьюрингу, по Черчу и по Маркову, раскрывающими соответственно аппаратные и функциональные и лингвистические аспекты понятия алгоритма. С помощью понятий недетерминированной машины Тьюринга проводится разделение алгоритмических проблем по трудоемкости.

В результате освоения материалов курса студенты обучаются основным приемам представления и исследования функций алгебры логики приобретают практические навыки построения формальных алгоритмических моделей. Учащиеся должны уметь выделять основные элементы описания алгоритмической проблемы, правильно ориентироваться в вопросах вычислительной сложности алгоритмов.

Изучаемый курс закладывает математические основы, необходимые при освоении теории кодирования, теории автоматов, методов структурного синтеза импульсных устройств, а также методов автоматизации проектирования вычислительных систем

Студенты технических факультетов МТУСИ в течение третьего семестра выполняют одну контрольную работу, в которой должны быть выполнены задания 1-3 и сдают экзамен.

Бюджет времени (в часах)

Аудиторная работа	Самостоятельная работа
лекции	упражнения	итого	изучение курса	выполнение контрольных работ	итого

Рабочая программа

1. Функции алгебры логики (ФАЛ). Способы задания ФАЛ. Эквивалентность двух функций. Количество различных ФАЛ от n переменных.
2. Основные 2-местные и 1-местные функции алгебры логики. Связь ФАЛ с импульсными элементами.
3. Совершенная дизъюнктивная нормальная форма. Алгоритм построения.
4. Совершенная конъюнктивная нормальная форма. Алгоритм построения.
5. Полином Жегалкина. Алгоритм построения.
6. Базисные наборы функций алгебры логики. Эквивалентность басисов. Представление ФАЛ в различных базисах
7. Существенные и несущественные логические переменные. Процедура определения существенности.
8. Минимизация функций алгебры логики по Карно-Вейчу. Процедура минимизации.
9. Минимизация произвольной дизъюнктивной формы или произвольной конъюнктивной формы. Процедура минимизации.
10. Предикаты. Кванторы.
11. Понятие алгоритма и связанных с ним категорий
12. Машина Тьюринга (МТ). Операции над МТ.
13. Другие формальные системы описания алгоритма
14. Недетерминированная МТ
15. Размерность и трудоемкость задачи. Классы вычислительной сложности

Математическая логика

Понятие двоичной функции и способа ее задания.

Математической логикой называется раздел математики занимающийся изучением общих законов построения и применения двоичных функций. Двоичной функцией 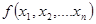от n - двоичных переменных называется функциональное всюду определенное и (как правило) всюду значимое соответствия вида

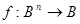, где каждая из переменных 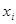, а также сама функция 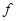принимают значения издискретного множества В, состоящего всего из 2 элементов .

Совокупность переменных 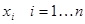, получивших определенное значение, в математической логике принято называть набором. Учитывая, что каждая из переменных 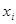может принимать в наборе всего лишь одно значение 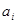(равное 0 либо 1) все возможные наборы 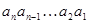, образующие область определения функции 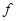, легко могут быть перечислены. Такое перечисление обычно принято производить в естественном порядке. Например, в таблице 1, приведено в естественном порядке перечисление набров из 3-х переменных.

Ясно, что двоичная функция от n - переменных будет определена на 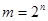наборах, т.к. каждому набору может быть однозначно сопоставлен его номер p в диапазоне от 0 до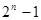

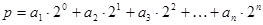
Можно сказать, что набор переменных представляет свой номер в виде двоичного числа. А естественный порядок наборов соответствует расстановке наборов по возрастанию их номеров.

Таблица 1

р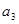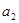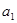

Функциональность соответствия 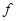означает, что любому конкретному набору переменных будет соответствовать не более одного значения функции. Определение значений двоичной функции на наборах называется таблицей истинности функции.

Т.к. значениями 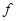могут быть опять таки 0 либо 1, то количество различных функций от n - переменных будет равно 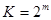, где m – количество наборов, или, подставляя количество наборов -