Синтез логических схем на элементах комбинационного типа.
ОСНОВЫ МИКРОПРОЦЕССОРНОЙ ТЕХНИКИ
Методические указания
к лабораторному практикуму для студентов ЗГИА
специальности “Гидроэнергетика”
рекомендовано к изданию
на заседании кафедры
“Гидроэнергетика”
протокол №
от ” ”__________2007.
Запорожье
Основы микропроцессорной техники. Методические указания к лабораторному практикуму для студентов ЗГИА специальности «Гидроэнергетика» (7.090503). Разраб. В. В. Радченко, В. В. Назаренко, В. М. Чван,. – ЗГИА, 2007. - 58 с.
Разработал:
В. В. Радченко – зав. кафедры,
В. В. Назаренко – ассистент,
В. М. Чван – ст. преподаватель,
Ответственный за выпуск –
заведующий кафедрой «Гидроэнергетика»
доцент В. В. Радченко.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ…...………………………………………………………………..4
1. Цель работы…………………………………………………………………….4
2. Теоретическая часть……………………………………………………………5
2.1 Системы счисления………………………………………………………..5
2.2 Перевод чисел из одной системы счисления в другую…………………7
2.3 Двоичная арифметика……………………………………………………11
2.4 Синтез логических схем на элементах комбинационного типа.
Элементы алгебры логики………………………………………………19
2.5 Минимизация функций алгебры логики с применением карты
Карно…………………………………………………………………..25
2.6 Система команд однокристального микропроцессора………………..28
3. Материалы, приборы, оборудование………………………………………..47
4. Указания по технике безопасности………………………………………….47
5. Порядок проведения лабораторного практикума…………………………..47
6. Содержание отчета……………………………………………………………50
7. Контрольные вопросы для самостоятельной проверки и контроля подготовки студентов к работе…………………………………………… 50
ЛИТЕРАТУРА.……………………………………………………………….51
ПРИЛОЖЕНИЕ А. Команды микропроцессора…….….………………….52
ВВЕДЕНИЕ
Целью разработки методических указаний является практическое освоение теоретической части курса дисциплины «Основы микропроцессорной техники.
Цифровое представление и цифровая обработка информации с применением микропроцессорной техники является неотъемлемой частью знаний для современного специалиста-энергетика. Знания в данной области необходимы для внедрения (эксплуатации) на предприятиях гидроэнергетики современных микропроцессорных систем управления технологическими процессами, применения промышленных микропроцессорных контроллеров и других вычислительных средств.
В настоящее время автоматизация управления технологическими процессами ведется на основе последних достижений микроэлектроники – микропроцессорной техники. Широкая номенклатура выпускаемых микропроцессоров, их многофункциональность и быстродействие позволяют успешно решать задачи автоматизации с многоуровневым управлением в рамках гибких автоматизированных систем.
Микропроцессор (МП) – программно-управляемое устройство, осуществляющее процесс обработки цифровой информации и управление им, построенное на одной или нескольких интегральных микросхемах.
Целью изучения дисциплины является изучение основ структуры, принципов управления и функционирования микропроцессора:
· элементов математического аппарата цифровой техники,
· базовых интегральных логических элементов, комбинационных цифровых устройств, последовательностных цифровых устройств,
· структуры МП, классификации, принципов управления,
· архитектуры типовых МП, системы команд.
.
1. ЦЕЛЬ РАБОТЫ
В процессе выполнения лабораторного практикума студент должен освоить:
- элементы математического аппарата цифровой техники;
- функции алгебры логики;
- анализ и синтез комбинационных цифровых устройств;
- метод упрощения выражений для функций алгебры логики с помощью карт Карно;
- минимизация заданной логической функции с применением средств
вычислительной техники;
- программную модель микропроцессора (МП);
- команды МП;
- принципы выполнения вычислений МП.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
2.1 Системы счисления.
Система изображения любых чисел с помощью ограниченного числа символов называется системой счисления. Используемые в системе счисления символы называются цифрами.
Существуют различные системы счисления, и от их особенностей зависит наглядность представления числа при помощи цифр и сложность выполнения арифметических операций. Если в системе счисления каждой цифре в любом месте числа соответствует одно и то же значение — количественный эквивалент, то такая система счисления называется непозиционной. Таким образом, для непозиционных систем счисления местоположение цифры в записи числа не играет никакой роли. Примером непозиционной системы счисления является римская система, в которой используются римские цифры I, V, X, L, С, М. Соответственно значение числа, например, CCXXIV вычисляется следующим образом: С=100, Х=10, V=5, 1 = 1. При этом вес цифры не зависит от ее местоположения в записи числа, а знак зависит. Если цифра с меньшим весом стоит слева от цифры с большим весом, то ее знак «—», а если цифра с меньшим весом стоит справа от цифры с большим весом, то еезнак «+». Общим недостатком непозиционных систем счисления являются трудности записи в таких системах больших чисел и трудности выполнения арифметических операций, поскольку для этого используются громоздкие правила. Поэтому в цифровой технике непозиционные системы практически не нашли применения.
В цифровой технике используются позиционные системы счисления. Система счисления называется позиционной,если одна и та же цифра имеет различное значение, которое определяется ее позицией в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции цифры по некоторому закону. В позиционных системах число
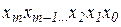
будет равно сумме
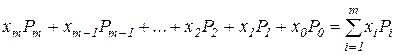
где 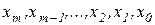 — символы, обозначающие целые числа;
— символы, обозначающие целые числа;
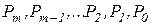 — веса,т.е. количественные значения каждой единицы, определяемые местом соответствующего символа в изображении числа. При изображении разных чисел в любой конкретной системе счисления символы
— веса,т.е. количественные значения каждой единицы, определяемые местом соответствующего символа в изображении числа. При изображении разных чисел в любой конкретной системе счисления символы
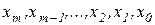 могут менять свое цифровое выражение, но веса единиц, расположенных на одних и тех же позициях во всех числах, сохраняют одно и то же заранее обусловленное значение. Номер позиции, который определяет вес единицы, расположенной на этой позиции, называется разрядом.
могут менять свое цифровое выражение, но веса единиц, расположенных на одних и тех же позициях во всех числах, сохраняют одно и то же заранее обусловленное значение. Номер позиции, который определяет вес единицы, расположенной на этой позиции, называется разрядом.
Среди позиционных систем особое значение имеют системы счисления, в которых вес отдельных разрядов представляет собой ряд членов геометрической прогрессии со знаменателем р. В этом случае число
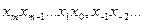
будет иметь значение
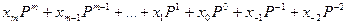
В этой последовательности запятая определяет целую часть числа от дробной, т.е. коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях. Запятая опускается, если нет отрицательных степеней. Число различных символов — цифр, необходимых для записи произвольного числа, равно знаменателю геометрической прогрессии р. В большинстве случаев используются числа натурального ряда 0, 1, 2, ..., (р—1). Знаменатель геометрической прогрессии р, равный отношению веса любого разряда к весу соседнего справа разряда, называется основанием системы счисления. Соответственно количество цифр, употребляемых в позиционной системе счисления, равно ее основанию.
В десятичной системе основание р = 10 и для записи чисел используется десять цифр: 0, 1,2,...,9. Каждая цифра числа занимает в нем определенный разряд, который имеет весовые коэффициенты для разрядов влево от запятой
100, 101, 102,... и вправо от запятой10-1, 10-2, 10-3,... Таким образом, запись 547,359 в десятичной системе счисления означает следующее количество:
547,359 = 5•102 + 4•101 + 7•10° + 3•10-1 + 5•10-2 + 9•10-3.
Позиционные системы счисления имеют ряд преимуществ перед непозиционными. Основным преимуществом следует считать удобство выполнения таких арифметических операций, как сложение, вычитание, умножение, деление, извлечение корня и др. Поэтому в цифровой технике, как правило, применяются позиционные системы счисления. Выбор основания системы счисления зависит от физических элементов, на основе которых строится то или иное устройство. В цифровой технике широко используются элементы с двумя устойчивыми состояниями. В этих элементах различие между отдельными фиксированными состояниями носит качественный, а не количественный характер, благодаря чему представление чисел с их помощью может быть реализовано значительно надежнее, чем с помощью элементов, в которых число четко различимых состояний превышает два. В частности, выполнение элемента с десятью четко различимыми состояниями представляет собой сложную техническую задачу. Указанное обстоятельство явилось одной из главных причин распространения в цифровой технике позиционных систем с недесятичным основанием, в первую очередь двоичной, а также восьмеричной и шестнадцатеричной систем счисления.
Наибольшее распространение в цифровой технике имеет двоичная система счисления. В этой системе используются только две цифры: 0 и 1. В двоичной системе любое число может быть представлено последовательностью двоичных цифр: 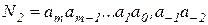
где аі принимает значение либо 0, либо 1. Эта запись соответствует сумме степеней числа два, взятых с указанными в ней коэффициентами
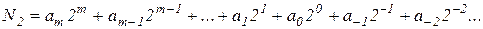
Вес разрядов, отсчитываемых влево от запятой, в целой части числа равен соответственно 1, 2, 4, 8, 16, ..., вес же разрядов правее запятой в дробной части будет ½, ¼, 1/8, 1/16. Например, число 11010,112 соответствует следующему количеству:
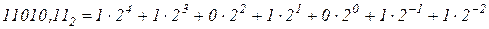
которое, как следует из приведенного разложения его по степеням числа 2, равно десятичному числу 26,7510. В восьмеричной системе счисления употребляется восемь цифр: 0, 1,2, ..., 7. Любое число в восьмеричной системе представляется последовательностью в которой цифры могут принимать значения от 0 до 7. Вес разрядов целой части 1, 8, 64, 256, ..., в дробной части 1/8, 1/64, 1/256. Например, восьмеричное число 756,25
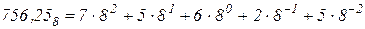
равно десятичному числу 494, 32812510.
В шестнадцатеричной системе счисления для изображения чисел употребляется 16 цифр: 0...15. При этом чтобы одну цифру не изображать двумя символами, приходится вводить специальные обозначения для цифр больше девяти. В качестве шести символов обычно используются буквы латинского алфавита: А, В, С, D, E, F, которым в десятичной системе соответствуют числа 10, 11, 12, 13, 14, 15. Таким образом, шестнадцатеричное число А7В,C816 соответствует следующему количеству:
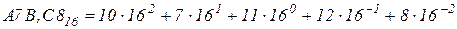
равному десятичному числу 2683,7812510.
2.2 Перевод чисел из одной системы счисления в другую.
Правила перевода чисел из двоичной системы в восьмеричную, шестнадцатеричную и обратно достаточно просты, поскольку основания восьми- и шестнадцатеричной систем счисления выражаются целой степенью двух (8=23, 16=24). Для перевода чисел из восьмеричной системы в двоичную достаточно каждую цифру восьмеричного числа представить трехразрядным двоичным числом — триадой. Например:
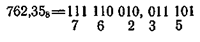
Перевод шестнадцатеричных чисел в двоичную систему счисления осуществляется представлением цифр шестнадцатеричного числа четырехразрядными двоичными числами — тетрадами. Например,
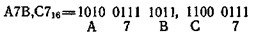
При обратном переводе чисел из двоичной системы в восьми- и шестнадцатеричную системы необходимо разряды двоичного числа, отсчитывая от запятой влево и вправо, разбить на группы по три разряда при переводе в восьмеричную систему или в группы по четыре разряда при переводе в шестнадцатеричную систему. Неполные крайние группы дополняются нулями. Затем каждая двоичная группа представляется цифрой той же системы счисления, в которую переводится число. Например,
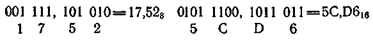
В общем случае, при некратных основаниях, перевод числа, содержащего целую и дробную части,
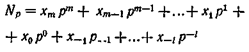
из системы с основанием p1в систему с основанием р2можно выполнить по универсальному алгоритму, при котором целая и дробная части приводятся к следующему виду:
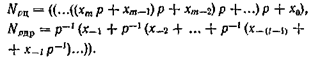
Согласно этому алгоритму перевод числа состоит из вычислительных процессов двух видов:
· последовательного деления целой части и образующихся целых частных на основание новой системы счисления,
· 2) последовательного умножения дробной части и дробных частей получающихся произведений на то же новое основание, записанное, как и в первом случае, цифрами исходной системы счисления.
При переводе целой части числа остатки, получающиеся в результате процесса последовательного деления, представляют цифры а0, а1,... целой части числа в новой системе счисления, записанные цифрами исходной системы счисления. Последний остаток является старшей цифрой переведенного числа.
При переводе дробной части числа целые части, получающиеся при каждом умножении, не участвуют в последующих умножениях. Они представляют цифры в дробной части исходного числа в новой системе счисления, изображенные цифрами исходной системы. Значение первой целой части является первой цифрой после запятой переведенного числа.
При преобразовании десятичных чисел в двоичные целая часть должна последовательно делиться на 2, а дробная часть — умножаться на 2. Например, при переводе десятичного числа 30,6 в двоичное получим целую часть путем деления:
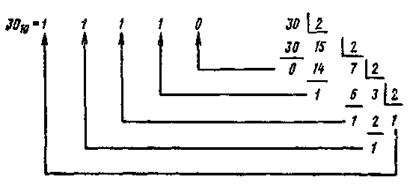
и дробную часть путем умножения на 2:
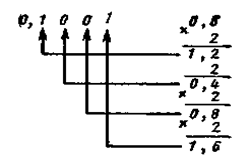
В результате имеем двоичное число 11110, 1001... Если при переводе дробной части получается периодическая дробь, то производится округление, исходя из заданной точности вычисления. В данном примере дробь определена с точностью до пятого знака после запятой.
Аналогично осуществляется перевод чисел из двоичной системы в десятичную. Например, при переводе двоичного числа 111101, 01 в десятичное его целую часть надо делить на основание десятичной системы, которое в двоичной записи будет 10102, а дробную умножать последовательно на это число:
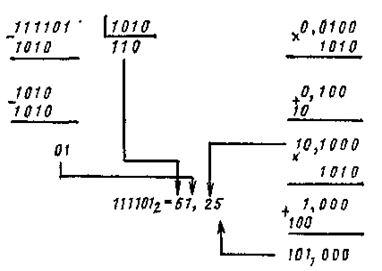
При переводах чисел по рассмотренному алгоритму необходимо выполнять последовательные преобразования, пользуясь таблицями сложения и умножения исходной системы счисления. При переходе вручную к системе с большим основанием такой процесс оказывается неудобным. Поэтому в этом случае применяется другой алгоритм. Сначала для первых чисел находится произведение старшего разряда числа на основание исходной системы счисления, к которому прибавляется следующая цифра переводимого числа. Затем полученная сумма также умножается на основание р, кполученному произведению прибавляется следующая цифра, и т. д. до последнего цикла, в котором осуществляется только прибавление цифры младшего разряда без последующего умножения. При этом действия выполняются в новой системе счисления.
Аналогичная последовательность действий применяется и для перевода дробной части, с той лишь разницей, что для умножения используется величина, обратная основанию и равная р-1. Например, при переводе двоичного числа 111101,101 в десятичную систему
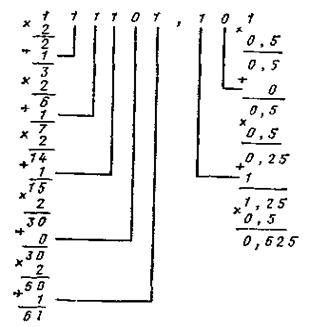
В результате получаем десятичное число 61,625.
Пользуясь стандартным алгоритмом, можно переводить числа из десятичной системы в восьми- и шестнадцатеричные системы и обратно. При этом целая часть числа в десятичной системе последовательно делится на 16 или на 8, а дробная умножается соответственно на 16 или на 8. Например, при преобразовании десятичного числа 3951910 в шестнадцатеричную систему получаем число 9A5F16.

Применение шестнадцатеричной системы счисления позволяет переводить десятичные числа в двоичные и обратно. При этом вначале либо десятичное число переводится в шестнадцатеричное, либо шестнадцатеричное число заменяется двоичным. Например, для перевода числа 50910 в двоичную систему сначала оно должно быть преобразовано в шестнадцатеричную систему
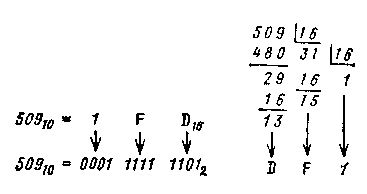
Аналогично осуществляется обратный перевод двоичных чисел в десятичные. Как видно из приведенного примера, при использовании промежуточного перехода к шестнадцатеричной системе счисления существенно сокращается количество операций деления, хотя и появляется дополнительно операция по преобразованию цифр шестнадцатеричной системы в двоичный код.
Двоичная арифметика.
Правила арифметики во всех позиционных системах аналогичны, и в двоичной позиционной системе счисления выполнение арифметических действий над двоичными числами задается с помощью таблиц двоичного сложения, вычитания и умножения. Основной операцией, которая используется в цифровых устройствах при выполнении различных арифметических действий, является операция алгебраического сложения чисел,т. е. сложения, в котором могут участвовать как положительные, так и отрицательные числа. Вычитание легко сводится к сложению путем изменения на обратный знак вычитаемого, а операции умножения и деления также сводятся к алгебраическому сложению и некоторым логическим действиям.
Сложение двух чисел в двоичной системе счисления выполняется на основе таблицы двоичного сложения:
0 + 0 = 0,
0 + 1 = 1,
1 + 0 = 1,
1 + 1 = 10.
Двузначная сумма в последнем случае означает, что при сложении двух двоичных цифр, равных 1, в каком-либо разряде двоичного числа возникает перенос в соседний старший разряд. Этот перенос должен быть прибавлен к сумме цифр, образовавшейся в соседнем разряде.
При сложении двух многоразрядных двоичных чисел цифры разрядов суммы формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы образуется суммированием цифр младших разрядов слагаемых. При этом кроме цифры разряда суммы формируется цифра переноса в следующий, более старший разряд, если оба младших разряда единицы. Таким образом, в разрядах, начиная со второго, могут суммироваться три цифры: цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего. Пример сложения двух многоразрядных двоичных чисел:
1 1 0 1 1 0 1 — первое слагаемое
+
1 0 0 1 1 1 1 — второе слагаемое
0 1 0 0 0 1 0 — поразрядная сумма без учета переносов
+
1 1 1 1 — переносы
10 1 1 1 1 0 0 — окончательная сумма
Непосредственно под двумя слагаемыми записан результат поразрядного сложения без учета переноса. В тех разрядах, в которых оба слагаемых равны единице, поразрядная сумма равна 0. В этих разрядах образовался перенос в соседний старший разряд, который отмечен в следующей строке. В результате сложения строки поразрядных сумм со строкою переносов получается окончательная сумма. При сложении поразрядной суммы с переносами удобно пользоваться следующим правилом: если в результате поразрядного суммирования образовалась группа единиц, расположенных рядом, и в младший разряд этой группы поступает перенос 1, то он переводит все единицы этой группы в нули, а ближайший за рядом единиц 0 — в 1. Это правило можно использовать при сложении следующих чисел:
1 0 1 1 0 1 0 0 1 — первое слагаемое
+
1 1 0 0 1 1 1 1 1 — второе слагаемое
0 1 1 1 1 0 1 1 0 — поразрядная сумма
+
1 1 1 — переносы
1 1 0 0 0 0 1 0 0 0 — окончательная сумма
Использование этого правила позволяет ускорить формирование окончательной суммы.
Вычитание двух чисел в двоичной системевыполняется на основе таблицы двоичного вычитания:
0 — 0 = 0,
1 — 0 = 1,
1 — 1 = 0,
10—1 = 1.
Если при поразрядном вычитании приходится вычитать из нуля в уменьшаемом единицу в вычитаемом, то делается заем в соседнем старшем разряде, т. е. единица старшего разряда представляется как две единицы данного разряда. Вычитание в этом случае выполняется в соответствии с таблицей. Если в соседнем разряде или в нескольких старших разрядах стоят нули, то заем делается в ближайшем старшем разряде, в котором стоит единица. Эта единица представляется в виде суммы числа, состоящего из единицы во всех промежуточных разрядах, в которых находились нули, и двух единиц в данном разряде. Далее производится поразрядное вычитание в соответствии с таблицей. Естественно, что необходимости в дополнительном заеме во всех промежуточных разрядах появиться не может. Например, при вычитании чисел
1 1 1 0 0 0 1 1 — уменьшаемое
__1 1 0 1 1 (11) 1 1 — уменьшаемое с учетом заема
1 0 0 1 0 1 1 0 — вычитаемое
0 1 0 0 1 1 0 1 — разность
В цифровой технике операция вычитания с использованием заема практически не применяется (за исключением отдельных устройств) и реализуется как алгебраическое сложение с применением специальных кодов для представления отрицательных чисел. При этом операция вычитания сводится к операции простого арифметического сложения при помощи обратного и дополнительного кодов, используемых для представления отрицательных чисел.
Обратный кодотрицательных двоичных чисел может быть сформирован по следующему правилу: цифры всех разрядов, кроме знакового, заменяются на обратные (инвертируются) — единицы заменяются нулями, а нули единицами. В знаковый разряд ставится единица Обратное преобразование из обратного кода в прямой производится по тому же правилу. При использовании обратного кода операция вычитания реализуется как арифметическое сложение положительного числа, представленного в прямом коде, с отрицательным числом, представленным в обратном коде. Например, при вычитании из числа 10110 числа 01101 уменьшаемое представляется как положительное число в прямом коде 0 10110, а вычитаемое— как отрицательное число в обратном коде 1 10010. В представлении чисел знаковые разряды выделены полужирным шрифтом. При выполнении операции арифметического сложения над этими числами получаем алгебраическую сумму

Перенос, возникающий из знакового разряда, при использовании обратного кода должен прибавляться в младший разряд суммы. В данном примере уменьшаемое по модулю больше вычитаемого, поэтому алгебраическая сумма положительная и представлена в прямом коде. При изменении знаков слагаемых в приведенном примере на обратные
1 01001 — первое слагаемое в обратном коде
+
001101 — второе слагаемое в прямом коде
1 10110 — сумма в обратном коде
результатом сложения будет отрицательное число и оно будет представлено в обратном коде.
Дополнительный кодотрицательных двоичных чисел может быть сформирован по следующему правилу: цифры всех разрядов, кроме знакового, инвертируются, и в младший разряд прибавляется единица. Дополнительный код может быть получен и из обратного путем прибавления единицы к младшему разряду обратного кода. При этом в знаковый разряд отрицательного числа в дополнительном коде ставится единица. Обратное преобразование из дополнительного кода в прямой производится по тому же правилу.
При использовании дополнительного кода для вычитания двоичных чисел из предыдущего примера получим
0 10110 — первое слагаемое в прямом коде
+
1 10011 — второе слагаемое в дополнительном коде
0 01001 — сумма в прямом коде
При сложении складываются цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса. Алгебраическая сумма, полученная в результате сложения, является положительным числом и поэтому представлена в прямом коде. Если знаки слагаемых меняются на обратные:
1 01010 — первое слагаемое в дополнительном коде
+
0 01101 — второе слагаемое в прямом коде
1 10111 — сумма в дополнительном коде
то результат сложения есть отрицательное число и оно оказывается представленным в дополнительном коде.
При алгебраическом сложении двоичных чисел в образовавшейся сумме возможно переполнение разрядной сетки, которое заключается в том, что результат операции — сумма содержит большее число разрядов, чем число разрядов в устройстве, предназначенном для их хранения. Для выявления переполнения разрядной сетки используется модифицированный код. В нем два знаковых разряда и в обоих разрядах положительные числа содержат нули, а отрицательные числа — единицы. Выполнение операций суммирования с использованием модифицированного дополнительного или модифицированного обратного кода производится по сформулированным выше правилам. Если результат суммирования содержит в знаковых разрядах комбинации 01 или 10, то это служит признаком переполнения разрядной сетки. Например, при сложении чисел
00 11011 — первое слагаемое в прямом модифицированном коде
+
11 01011 — второе слагаемое в дополнительном модифицированном коде
00 00110 — сумма в прямом модифицированном коде
Переполнения разрядной сетки не возникает. Перенос из старшего знакового разряда отбрасывается. При сложении чисел 00 10110 и 00 11011
00 10110
+
0011011
01 10001
в знаковых разрядах результата суммирования возникает комбинация 01, что свидетельствует о переполнении разрядной сетки и ошибочности зафиксированного результата. Возникновение ошибки связано с тем, что при суммировании положительных чисел перенос из старшего разряда оказался зафиксированным во втором из знаковых разрядов. Для регистрации результата суммирования в данном примере требуется шесть разрядов (кроме знаковых). При суммировании отрицательных чисел также возможно переполнение разрядной сетки;
11010011
+
11100011
10110110
В этом случае комбинация 10 в знаковых разрядах указывает на переполнение разрядной сетки.
Умножение двоичных многоразрядных чиселвключает в себя операции — определение знака произведения и определение его абсолютной величины. Знаковый разряд может быть получен суммированием цифр знаковых разрядов сомножителей без формирования переноса:
0 + 0 = 0,
0 + 1 = 1,
1 + 0 = 1,
1 + 1 = 0 без формирования переноса
При несовпадении цифр получается 1, что соответствует знаку произведения двух сомножителей с разными знаками.
Абсолютная величина значения произведения определяется путем перемножения чисел без учета их знаков. Перемножение многоразрядных двоичных чисел производится на основе таблицы двоичного умножения
0 x 0 = 0,
0 x 1 = 0,
1 х 0 = 0,
1 х 1 = 1.
При умножении двух двоичных чисел множимое последовательно умножается на каждую цифру множителя, начиная либо с младшей, либо со старшей, и для учета веса соответствующей цифры множителя сдвигается либо влево, если умножение производится, начиная с младшего разряда множителя, либо вправо, если умножение производится, начиная со старшего разряда множителя, на такое число разрядов, на которое соответствующий разряд множителя сдвинут относительно младшего или старшего разряда.
Получающиеся в результате умножения и сдвига частичные произведения после суммирования дают полное произведение. Особенность умножения двоичных чисел состоит в том, что частичное произведение может быть либо сдвинутым на соответствующее число разрядов множимым, если соответствующая цифра множителя равна 1, либо нулем, если соответствующая цифра множителя равна 0:
10111 — множимое
______1101 — множитель
10111 — первое частичное произведение
00000 — второе частичное произведение
10111 — третье частичное произведение
10111_____— четвертое частичное произведение
100101011 — произведение
Тот же результат можно получить при умножении, начиная со старших разрядов множителя:
х 1101
10111
В цифровых устройствах процессу суммирования частичных произведений придают последовательный характер: формируется одно из частичных произведений, к нему с соответствующим сдвигом прибавляется следующее частичное произведение, к полученной сумме прибавляется с соответствующим сдвигом очередное частичное произведение, и т. д., пока не окажутся просуммированными все частичные произведения и не будет получено полное произведение.
Пример умножения чисел этим методом:
10111 — четвертое частичное произведение
101110 — сдвиг на разряд влево
_10111 — третье частичное произведение
1000101 —прибавление третьего частичного произведения
10001010 — сдвиг на разряд влево
00000 — второе частичное произведение
10001010 — прибавление второго частичного произведения
100010100 — сдвиг на разряд влево
10111 — первое частичное произведение
100101011 — прибавление первого частичного произведения
При таком методе все частичные произведения суммируются с требуемыми сдвигами друг относительно друга, благодаря чему образуется ранее приведенный результат умножения этих чисел.
При умножении дробных чисел меньше единицы умножение удобнее начинать с младшего разряда множителя. Так, при перемножении дробных чисел 0,10111 и 0,1101 получим
0,10111: — первое частичное произведение
0,01011: 1 — сдвиг на разряд вправо
+
00000: — второе частичное произведение
0,01011: — прибавление второго частичного произведения
0,00101: 11 — сдвиг на разряд вправо
+
10111: — третье частичное произведение
0,11100: 11 — прибавление третьего частичного произведения:
0,01110: 011 — сдвиг на разряд вправо
+
10111: — четвертое частичное произведение
1,00101: 011 — прибавление четвертого частичного произведения
0,10010: 1011— сдвиг на разряд вправо
Если требуется сохранить все разряды в произведении, то в разрядной сетке устройства должно быть предусмотрено число разрядов, равное сумме числа разрядов множимого и множителя. Однако при умножении дробных чисел часто в произведении требуется иметь то же число разрядов, что и в множимом. В таком приближенном представлении результата не фиксируются цифры разрядов при сдвигах, выдвигаемые правее вертикальной штриховой линии, показанной в приведенном выше примере. Таким образом, цифры младших разрядов окажутся потерянными и будет получен приближенный результат 0,100101. Далее отбрасывается последний из разрядов, и если этот разряд содержит 1, то 1 прибавляется к следующему разряду для округления результата. Следовательно, полученный результат 0,10011.
Если множимое, или множитель, или оба вместе содержат и целую и дробную части, то запятые в множимом и множителе не учитываются, они умножаются как два целых числа и от полученного произведения справа отделяются запятой т+п разрядов, где п — число дробных разрядов множимого, a m — число дробных разрядов множителя.
Деление двоичных многоразрядных чиселвключает в себя две операции — определение знака частного и определение его абсолютной величины.
Знаковый разряд частного может быть получен, как и знаковый разряд произведения, суммированием цифр знаковых разрядов делимого и делителя без формирования переноса. Абсолютная величина частного определяется делением чисел без учета их знаков.
Деление начинается с того, что от делимого слева отделяется группа разрядов, причем количество разрядов в этой группе должно либо равняться количеству разрядов в делителе, либо быть на один разряд больше. Если отделение такой группы возможно, в старший разряд частного записывается 1, в противном случае в разряд единиц частного записывается нуль. Если выявилось, что частное содержит целую часть, то образуется новая группа разрядов путем вычитания из выделенной группы делителя и приписывания к разности очередной цифры делимого. Если в результате получилось число, превышающее делитель, то в частное записывается 1, в противном случае следующая цифра будет равна 0.
В дальнейшем выполняется ряд одинаковых циклов. Если последняя цифра частного была равна 1, то новая группа образуется вычитанием делителя из предыдущей группы и приписыванием очередной цифры делимого. Если последняя цифра частного 0, то для образования новой группы достаточно приписать к предыдущей группе очередную цифру делимого. Последняя цифра целой части частного получается тогда, когда после определения очередной цифры частного 1 или 0 в делимом не останется больше цифр для того, чтобы приписывать их к разности между предыдущей группой и делителем или к самой предыдущей группе. После этого начинается выделение дробных членов частного. Оно отличается от вычисления целых членов только тем, что вместо очередных цифр делимого к предыдущим группам приписываются нули.
Рассмотрим примеры, в которых делимое больше и меньше делителя:
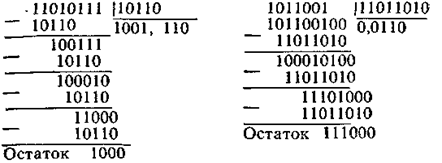
В цифровых устройствах при выполнении операции деления так же, как и при выполнении операции алгебраического сложения, используется дополнительный и модифицированный коды. Например, при делении числа 0,11011 на 0,11101 представляем делитель в дополнительном коде 00011:
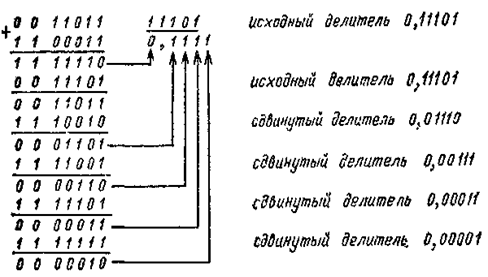
При вычитании сдвинутые делители представляются в дополнительном коде.
Для ускорения деления используется деление без восстановления остатка.При этом способе допускаются как положительные, так и отрицательные остатки при вычитании делителя. Если очередной остаток положителен, то в частное пишется 1, а на следующем цикле работы делитель вычитается из сдвинутого на один разряд влево остатка. Если же очередной остаток отрицателен, то в частное пишется 0, а на следующем цикле работы делитель прибавляется к сдвинутому на один разряд влево остатку.
Например, при делении числа N1= 10011 на число N2=0,11001 по способу без восстановления остатка при переходе к модифицированным дополнительным кодам получим N1 = 00 10011, N2=0011001,
—N2=11 100111:
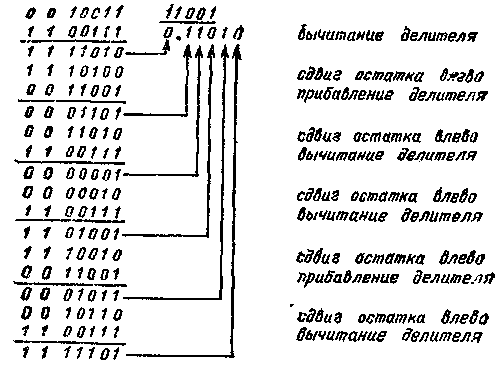
Как видно из приведенных примеров, деление является весьма трудоемкой операцией. В ряде случаев в цифровых устройствах эта операция заменяется нахождением обратной величины делителя по специальной подпрограмме и последующим умножением делимого на найденную обратную величину делителя, которая вычисляется приближенно на основе какой-либо быстро сходящейся итерационной формулы.
Синтез логических схем на элементах комбинационного типа.
Элементы алгебры логики.
Для описания комбинационных схем (КЦУ) используется математический аппарат булевых функций – алгебра логики. Переменные х1,х2, …, хn называются двоичными, если они могут принимать только значения: 0 или 1.
Функция от двоичных переменных f ( х1,х2,…,хn ) называется булевой, если она, также как и ее аргумент, принимает только два значения: 0 или 1. Связи между входными и выходными сигналами в комбинационных схемах аналитически описываются булевыми функциями. Существуют различные способы задания или представления булевых функций: словесное описание функций, табличный способ (функция представляется в виде таблиц истинности), алгебраический способ, при небольшом количестве переменных – с помощью карт Карно.
От таблиц истинности можно перейти к алгебраической форме представления функций. В такой форме удобно производить различные преобразования функций, например с целью их минимизации. Основные булевы функции одной и двух переменных, их обозначение и наименование приведены в таблице 2.1, графическое изображение на рис.2.1.
Таблица 2.1. - Основные функции алгебры логики для одной и двух переменных
| Функции | Аргумент Х=0 У=0 | Аргумент Х=0 У=1 | Аргумент Х=1 У=0 | Аргумент Х=1 У=1 | Обозначение функции | Наименование функции |
| F1(x) | Константа «0» | |||||
| F2(x) | Константа «1» | |||||
| F3(x) | x | Переменная «х» | ||||
| F4(x) | 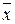 | Инверсия | ||||
| F5(x.y) | 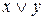 | Дизъюнкция ИЛИ | ||||
| F6(x.y) | 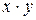 | Конъюнкция И | ||||
| F7(x.y) | 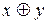 | Сложение по модулю 2 | ||||
| F8(x.y) | 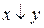 , ( , ( 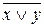 ) ) | Стрелка Пирса (ИЛИ-НЕ) | ||||
| F9(x.y) | 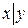 , ( , ( 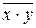 ) ) | Штрих Шеффера (И-НЕ) | ||||
| F10(x.y) |  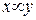 | Равнозначность |
ИЛИ И НЕ
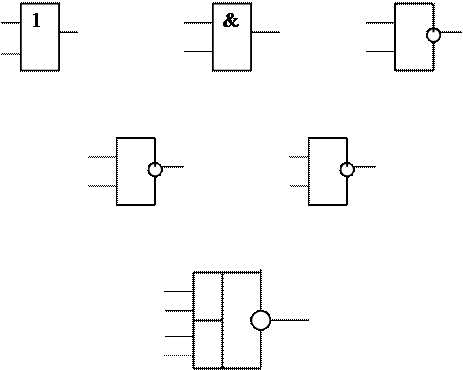 |
х1 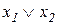 х1
х1 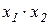 х1
х1 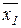
х2 х2 х2
ИЛИ-НЕ И-НЕ
х1 1 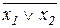 х1 &
х1 & 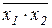
х2 х2
И-ИЛИ-НЕ
х1 & 1
х2 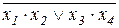
х3 &
х4
Рис.2.1 - Графическое обозначение ЛЭ на схемах
