Примеры бинарных отношений. 2 страница

- указания характерных свойств элементов множества или характеристической функции множества (характеристическим предикатом);

- заданием порождающей процедуры.

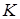При заданном характеристическом (определяющем) свойстве и заданном классе элементов (универсальном множестве для решаемой задачи) множество определяется как множество, которое содержит все элементы из 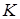, обладающие свойством . Для определения по схеме свертывания используется следующая запись .

Пример. Множество четных чисел можно определить как или как , где через обозначено множество целых чисел.

– множество граждан Украины.

– множество слонов.

Свойства, которыми должны обладать элементы формируемого множества , можно описать характеристической функцией (характеристическим предикатом) 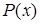. Обычно 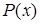– это высказывание, в котором что-то утверждается об , или некоторая функция переменной . Тогда множество можно представить как . Если класс 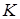указан явно, то в этом случае используется запись . Если при замене на 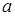высказывание становится истинным или функция в заданной области определения удовлетворяется, то 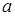есть элемент данного множества. Таким образом , если истинно.

Пример.

а) – множество чисел, квадрат которых равен двум;

б) – множество чисел, квадрат которых плюс единица больше нуля.

Множество может быть также задано при помощи порождающей процедуры (рекурсивно) .

Определение.

Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определенного множества.

Пример.Множество нечетных чисел можно задать порождающей процедурой .

Множество можно задать рекурсивной процедурой .

При задании множеств могут возникать ошибки и противоречия, поэтому к описанию свойств множеств и их элементов естественно предъявлять требование точности и недвусмысленности. Множество задано корректно, если для любого элемента можно определить, принадлежит он множеству или нет.

Пример.Определение множества как множества, содержащего любые пять натуральных чисел, не является корректным, поскольку невозможно определить точно элементы .

Множество всех простых чисел определено корректно. Для любого натурального числа можно проверить, является ли оно простым, хотя практически на это может потребоваться очень много времени.

Пример. Множество всех хороших фильмов 2011 года разные люди зададут разными списками (может быть пустыми). Сами критерии, по которым производится отбор, при этом будут различны. Такое множество нельзя считать строго заданным.

Неограниченное применение схемы свертывания, некорректность задания множества, свободное использование понятий интуитивного теоретико-множественного универсума иногда ведет к противоречиям, которые называются логическими парадоксами (парадокс Рассела, парадокс Кантора, парадокс Банаха-Тарского) и изучаются в математической логике.

Пример.

Можно получить «множество всех множеств» . Если считать множеством, то получаем .

1.7 Множество и подмножество

Определение. Множество , все элементы которого принадлежат и множеству , называется подмножеством(частью)множества . При этом говорят, что содержит или покрывает .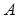

Это отношение между множествами называют включением и обозначают символом , т.е. ( включено в ) или ( включает ).

Если не является подмножеством , это записывается как . Таким образом, , если существует элемент , не принадлежащий .

Пример:

а) множество конденсаторов электронной цепи является подмножеством всех её компонентов;

б) множество положительных чисел – это подмножество множества действительных чисел.

в) ;

г) .

Пример. Книга из множества книг в шкафу может рассматриваться как множество страниц. Следует обратить внимание на то, что речь идет об элементах множества, а не о подмножествах, т.к. никакая совокупность страниц не может рассматриваться как подмножество множества книг.

Множества и равны , если их элементы совпадают. Иначе говоря, тогда и только тогда, когда и .

Пример. Если есть множество , а 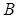есть множество , тогда и – равные множества.

Определение.

Если и , то часто называется собственным, строгим или истинным подмножеством .Записывается данное отношение как , где 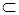знак строгого включения.

Пример.Пусть ; , тогда ясно, что и – собственное (истинное) подмножество .

В частности, каждое множество есть подмножество самого себя. Принято также считать, что пустое множество 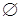является подмножеством любого множества. Поэтому, любое непустое множество имеет, по крайней мере, два различных подмножества: само и пустое множество .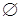

Эти подмножества называются несобственными, а все другие подмножества называются собственными. Если требуется различать собственные и несобственные подмножества, то для обозначения включения собственных подмножеств используется знак ( ), а для несобственных – ( ).

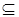Конечно, собственные подмножества образуются всевозможными сочетаниями по одному, два, три и т.д. элементов данного множества.

Пример: ; ; ; ; ; ; . , где .

Определение. Множество всех подмножеств множества , или булеанмножества , обозначаемый (или ), есть множество, состоящее из всех подмножеств множества . Множество называется также множеством-степенью.

Пример. Так, для трёхэлементного множества булеан имеет вид .

В случае конечного множества , состоящего из n элементов, множество подмножеств содержит элементов, т.е. .

Пустое множество имеет только одно подмножество – само пустое множество, поэтому .

1.8. Контрольные вопросы и задания

1. Что такое множество? Приведите примеры различных множеств.

2. Какие способы задания множеств Вы знаете?

3. Что такое пустое множество? Обоснуйте необходимость использования пустого множества.

4. Что такое универсальное множество? Приведите примеры универсального множества.

5. Дайте определение конечного и бесконечного множества.

6. Дайте определение счетного множества.

7. Что такое мощность множества?

8. Дайте определение подмножества. Приведите примеры подмножеств.

9. Какое отношение между множествами называют строгим включением?

10. Чем отличается понятие включения ( 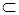или 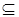) от понятия принадлежности ( )?

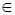11. В каких случаях можно говорить, что множества , и 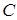равны?

12. Поясните понятие «булеан множества ». Приведите примеры булеана.

Лекция 2 Алгебра множеств

2.1 Геометрическая интерпретация множеств. Круги Эйлера и диаграммы Венна

Для наглядного представления отношений между подмножествами универсального множества 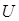используются диаграммы Венна и круги Эйлера.

Построение диаграммы Венна заключается в разбиении плоскости на ячеек с помощью фигур, каждая из которых представляет на диаграмме отдельное множество, а – число изображаемых множеств.

Плоскость, на которой изображаются фигуры, представляет универсальное множество. Чаще всего универсальное множество при этом изображают в виде прямоугольника, а его подмножества изображают в виде кругов (кругов Эйлера), находящихся внутри прямоугольника.

С помощью диаграмм Эйлера-Венна можно графически показать, принадлежит ли некоторый элемент рассматриваемым множествам или нет, однако реальные отношения включения, установленные между множествами, отразить нельзя. Можно рассматривать отношения включения только в общем случае.

Пример.На рис. 1.1 элемент 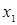принадлежит и не принадлежит ; принадлежит и ; принадлежит и не принадлежит ; не принадлежит ни , ни . Любой элемент принадлежит универсальному множеству .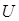

Рисунок 1.1 – Диаграмма Венна для двух множеств и

Индивидуальные отношения между заданными множествами изображают с помощью кругов Эйлера. В этом случае множества, не имеющие общих элементов, изображают фигурами (чаще кругами), которые не пересекаются (рис. 1.2).

Рисунок 1.2 – Изображение множеств, не имеющих общих элементов, с помощью кругов Эйлера

Множества, имеющие общие элементы, изображают пересекающимися фигурами (рис. 1.3).

Рисунок 1.3 – Изображение множеств, имеющих общие элементы, с помощью кругов Эйлера

Отношение включения на множествах изображают, располагая одну фигуру вложенной в другую (рис. 1.4).

Рисунок 1.4 – Изображение отношения включения на множествах с помощью кругов Эйлера

2.2 Операции на множествах

В теории множеств определяются способы конструирования новых множеств из уже имеющихся при помощи операций над множествами. К таким основным (базовым) операциям на множествах относятся следующие операции: объединение, пересечение, разность, дополнение.

Рассмотрим операции на множествах.

Пусть имеются два множества и .

Определение. Объединением (суммой) множеств и называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств или . Объединение множеств и обозначается 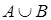. Данное определение можно записать .

Пример:

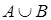а) если , а , тогда . Объединение образовано из 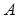и путем соединения вместе элементов и .

б) если , , то .

Аналогично определяется объединение произвольной (в том числе бесконечной) совокупности множеств. Если совокупность содержит небольшое количество множеств, то объединение данных множеств описывается явно, т.е. и т.д.

В общем случае используется обозначение , которое читается так: «объединение всех множеств , принадлежащих совокупности ».

Если же все множества совокупности занумерованы индексами, то используются другие варианты обозначений:

а)  для случая, когда ;

б)  для случая, когда – бесконечная совокупность и её множества занумерованы подряд натуральными числами;

в)  для случая, когда набор индексов множеств задан множеством .

Определение. Пересечением множеств и называется множество, состоящее из всех тех и только тех элементов, которые принадлежат и , и . Пересечение множеств и обозначается .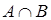

Сформулированное определение можно записать как . Если , то и – непересекающиеся множества.

Пример:

1. Если и , тогда .

2. Если и

, тогда

.

Аналогично определяется пересечение произвольной (в том числе бесконечной) совокупности множеств. Обозначение для пересечения системы множеств аналогичны приведенным выше обозначениям для объединения.

Определение.Система множеств, в которой все попарные пересечения множеств пусты, называется разбиениеммножества всех элементов этих множеств, а множества такой системы называются классами или блоками разбиения. Всякий элемент множества входит только в один класс разбиения.

Пример:

Множество всех групп направления (потока) «Компьютерные науки» является разбиением множества всех студентов, поступивших в университет на направление «Компьютерные науки». Классы этого направления – группы. Всякий студент может входить только в одну группу.

Определение. Разность и (обозначается 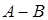или )  это множество, состоящее из тех и только тех элементов, которые принадлежат и не принадлежат , т.е. .

Пример: ; ; 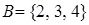тогда , .