Модель искусственного нейрона
Математическая модель нейрона (Рис.2.4.2) впервые была предложена Маккалоком и Питтсом (Warren McCulloch and Walter Pitts) в 1943.
«Математический» нейрон вычисляет взвешенную сумму его 
входных сигналов 
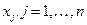, и генерирует выходное значение 
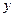равное 1, если взвешенная сумма превышает некоторый заданный порог 
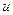. В противном случае 
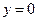. Таким образом, активационная функция математически записывается следующим образом:
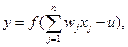(2.13)
где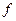 
- пороговая функция с заданным порогом (рис.2.38) и 
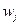- синаптический вес (synapse weight), связанный с входом 
.
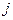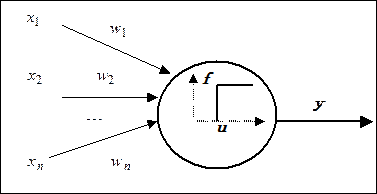
Рис. 2.38. Модель искусственного нейрона
Примечание. Активационную функцию называют также функцией активации или функцией срабатывания, передаточной функцией.
Часто формула (2.13) записывается как
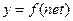, (2.14)
где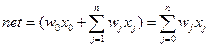 
и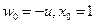 
.
Вход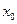 
называется «байесовским» входом (a bias). Таким образом, мы можем рассматривать (n +1) входов.
Дополнительный вход x0 и соответствующий ему вес используется для инициализации нейрона. Под инициализацией подразумевается смещение активационной функции нейрона по горизонтальной оси, то есть формирование порога чувствительности нейрона.
Эта модель может быть расширена многими путями, например, вводя различные функции активации так, как показано на рис. 2.39.
Рис. 2.39. Различные функции активации ИНС
Итак, искусственный нейрон (или математический нейрон Маккалока-Питтса, или формальный нейрон) — это узел ИНС, являющийся упрощённой моделью естественного нейрона. Математически, искусственный нейрон обычно представляют собой некоторую нелинейную функцию от единственного аргумента — линейной комбинации взвешенных входных сигналов. Полученный результат посылается на единственный выход.
От нейрона – к системе нейронов
Искусственные нейроны объединяют в сети — соединяют выходы одних нейронов с входами других. ИНС может рассматриваться в виде взвешенного направленного графа (weighted directed graph), вершины которого представлены нейронами, а направленные дуги (с весами) описывают связи между нейронами. ИНС характеризуется тремя параметрами: типом нейронов, архитектурой (организацией связей между нейронами) и алгоритмом обучения в данной сети. В настоящее время разработано большое множество моделей ИНС. Все они различаются по следующим пунктам:
· тип нейрона и тип вычисления в нем;
· математическая модель для представления и обработки информации в сети, включая алгоритм обучения;
· класс проблем, решаемых с помощью ИНС.
С учетом архитектуры ИНС могут быть разделены на два базисных класса:
· сети с прямым распространением сигнала (Feed-forward network), в структуре которых нет петель (циклов) и
· сети с обратным распространением сигнала или рекуррентные сети (Feedback network or Recurrent), в структуре которых есть циклы благодаря наличию обратных связей.
На рис. 2.40 показаны основные типы ИНС.
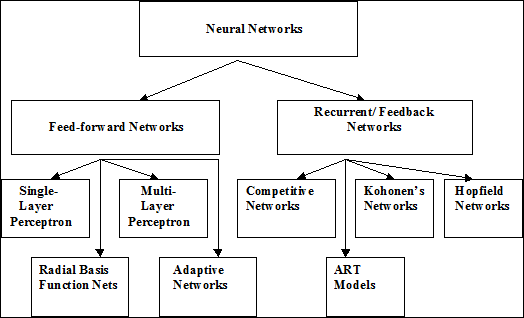
Рис. 2.40. Типы ИНС
Различные типы связей обуславливают различное поведение ИНС. «Ответ» (реакция) сети с прямой распространением сигнала на входную информацию не зависит от предыдущего состояния сети. Реакция сети с обратной распространением зависит от предыдущего состояния сети. Рассмотрим основные типы ИНС.